人工智能介绍
Posted eyoulc123
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能介绍相关的知识,希望对你有一定的参考价值。
0 前言
前一段时间,想做一个文本相似性的系统,用于比对两个句子的相似性,因此接触了一下机器学习。其中主要是看李宏毅老师的机器学习视频课程。但是机器学习太过于复杂,对于我来说,我估计还没有入门,只是看到机器学习这个大殿。 这篇文章,是对我之前学习的一个总结,也是我对于机器学习的一个理解。如果大家要系统的学习,建议看一下李宏毅老师的机器学习课程视频。
1. 人工智能几个名词
人工智能是一个很广的词,它包含了机器学习、专家系统等。 但是到了现在,大家一般提到人工智能指的就是神经网络、机器学习了。就象伟人一样,机器学习也经历了“三起三落”:
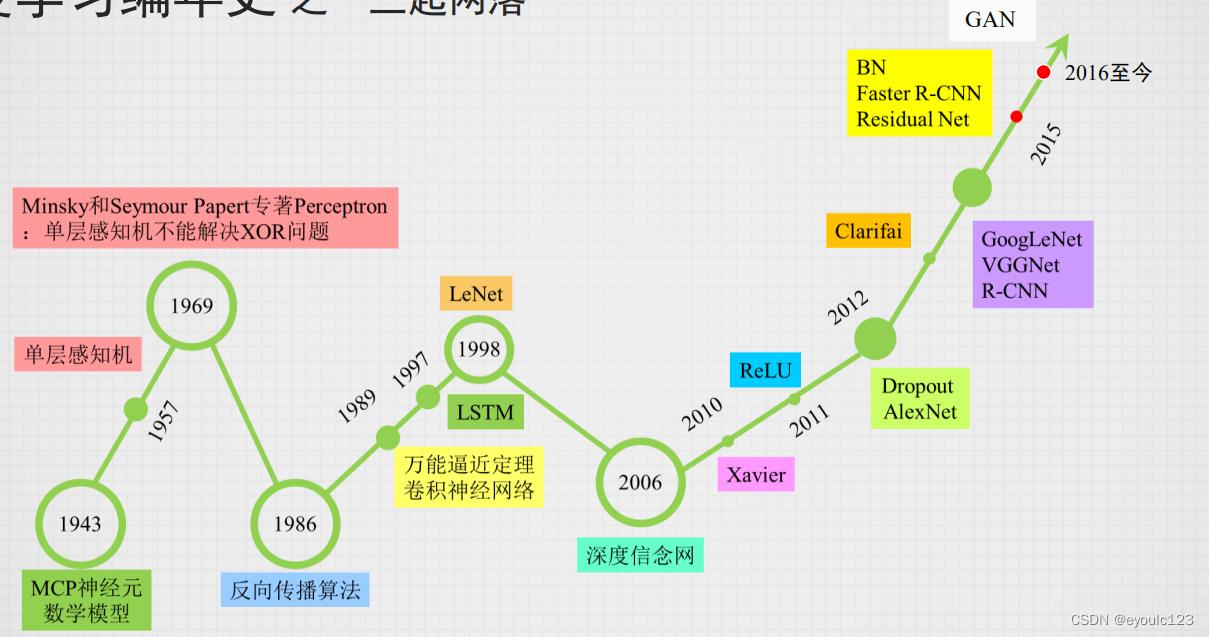
但是早期的时候,它并不是叫机器学习,而是以神经网络的名号来闯荡江湖。 但是随着XOR的问题提出,也宣判了神经网络的死刑。 在这后面很多年的时候,神经网络这个名声就开始变臭了,它的名声变臭到什么程度呢?只要文章中包含了“神经网络”这一个词,那篇文章就会被拒。 这怎么搞呢?没关系,给它再起一个名字,因此机器学习闪亮出场。
神经网络不是一个很新的技术,它出现的时间很早。 但是有一段时间,神经网络陷入了低谷,在这段时间,这个技术就变臭了,用台大李宏毅老师的话来说:神经网络象变成一个骂人的话,基本一有神经网络这个词,论文就会被拒绝。 后来随着技术的发展,人们发展神经网络还是可以解决很多问题的,但是“神经网络”这个词已经变臭了呀,这个时候人们又发明了一个新的词:机器学习。因此,我们可以这样子理解:机器学习 = 神经网络。
说完了机器学习与神经网络的关系,我们再具体说一下机器学习
2. 机器学习
总体来说,机器学习主要就是解决两个问题,或者说一个问题:回归问题。 对于回归,我不想讲解太多的内容。在这里,我们以一个简单的一元回归的问题,引入我们的分析。
2.1 一元线性回归问题
在我们中学的时候,我们经常会碰到这样子的一个例子。
例:
为了统计某地的房价,统计了平米数与房价
样本 房价(万件) 制造费用(万元) 1 60 100 2 70 120 3 72 121 4 80 140 5 90 160 根据以上数据,计算出产量与制造费用的关系
这个问题,就是一个典型的一元线性回归的问题。我们将制造费用设为y,而产量为x,那么我们就需要求出一个类似于$y = bx + a$的函数,即为:
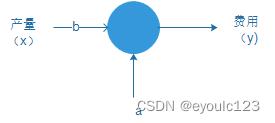
在中学的时候,我们学过一元线性回归方程的计算公式:
最
小
二
乘
法
计
算
公
式
:
b
^
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
(
y
i
−
y
ˉ
)
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
a
^
=
y
ˉ
−
b
^
x
ˉ
\\beginaligned & 最小二乘法计算公式:\\\\ & \\hatb = \\frac\\sum_i=1^n(x_i-\\barx)(y_i-\\bary)\\sum_i=1^n(x_i-\\barx)^2 \\\\ & \\hata = \\bary - \\hatb\\barx \\endaligned
最小二乘法计算公式:b^=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)(yi−yˉ)a^=yˉ−b^xˉ
那么上面的结果我们就可这样子计算出来:
- 计算平均值
x
ˉ
=
60
+
70
+
72
+
80
+
90
5
=
74.4
y
ˉ
=
100
+
120
+
121
+
140
+
160
5
=
128.2
\\beginaligned & \\barx = \\frac60+70+72+80+905 = 74.4 \\\\ & \\bary = \\frac100+120+121+140+1605 = 128.2 \\endaligned
xˉ=560+70+72+80+90=74.4yˉ=5100+120+121+140+160=128.2
3. 带入
b
ˉ
\\barb
bˉ公式计算
b
^
=
(
60
−
74.4
)
(
100
−
128.2
)
+
(
70
−
74.3
)
(
120
−
128.2
)
+
(
72
−
74.4
)
(
121
−
128.2
)
+
(
80
−
74.4
)
(
140
−
128.2
)
+
(
90
−
74.4
)
(
160
−
128.2
)
(
60
−
74.4
)
2
+
(
70
−
74.3
)
2
+
(
72
−
74.4
)
2
+
(
80
−
74.4
)
2
+
(
90
−
74.4
)
2
=
2.014
\\hatb = \\frac(60-74.4)(100-128.2) + (70-74.3)(120-128.2) + (72-74.4)(121-128.2)+ (80-74.4)(140-128.2) + (90-74.4)(160-128.2)(60-74.4)^2 + (70-74.3)^2 + (72-74.4)^2 + (80-74.4)^2 +(90-74.4)^2 = 2.014
b^=(60−74.4)2+(70−74.3)2+(72−74.4)2+(80−74.4)2+(90−74.4)2(60−74.4)(100−128.2)+(70−74.3)(120−128.2)+(72−74.4)(121−128.2)+(80−74.4)(140−128.2)+(90−74.4)(160−128.2)=2.014
4. 计算
a
ˉ
\\bara
aˉ:
a ˉ = y ˉ − b ^ x ˉ = 128.2 − 2.014 ∗ 74.4 = − 21.641 \\bara = \\bary - \\hatb\\barx = 128.2- 2.014*74.4 = -21.641 aˉ=yˉ−b^xˉ=128.2−2.014∗74.4=−21.641
- 写出方程: y ^ = 2.014 x ^ − 21.641 \\haty = 2.014\\hatx -21.641 y^=2.014x^−21.641
这个计算过程,是我们以前的方法,但是对于从事计算机的人员来说,这种优雅的方式,不是我们的风格。我们崇尚的“暴力出奇迹”,充分利用计算机的计算能力,随便给定一个a和b,然后不断的逼近它,使得它们的值最小。例如我让a = 1, b =1,然后,我们看结果:
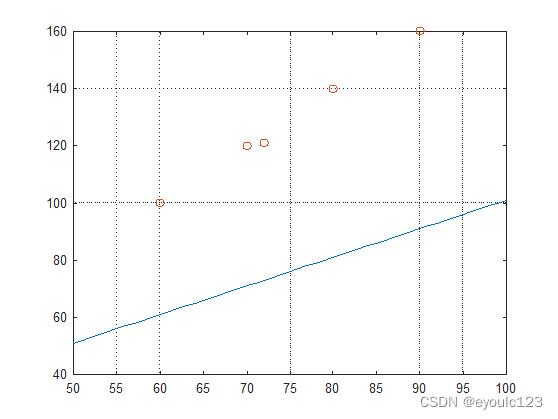
从上面的图中,我们就可以看到a和b的值不合理,我们需要将整条直接往上移一下,然后尝试改变a的值,同时斜率也感觉不符合相求,最后不断的变化,直接到找到一个符合我们要求的值。

至我们如何判断a与b的值是否合适,这里就涉及到一个处理方式:梯度下降的方法。大家只需要知道,有一个固定的方法,通过这个固定的方法,我们可以知道对应的a与b是往大调,还是往小调。 通过这种方法,我们不断的逼近我们的散点。最终得到一个符合我们要求的方式。
最终的函数,我们可以得到一个,当我们输入的x = 5时,我们就会发现一个问题 房价为-1.5,房价不可能为负值。因此一般在最后的输出的时候,增加一个修改函数。 整体就变成了:
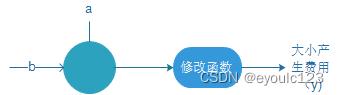
其实这个修改函数,有一个专业的名词:激活函数(不知道它为啥叫激活函数,但是我一直感觉它的作用就是对结果值进行修正。后面我们也称它为激活函数)。常用的也只有几个。一个叫ReLU函数,一个是Sigmod函数。 下面是它们两个的函数图形。如果懒得看,可以直接跳过。 我们只需要记住,它们的作用就是对于预测函数的数值进行一个修改,让它更靠谱一些。
ReLU函数:
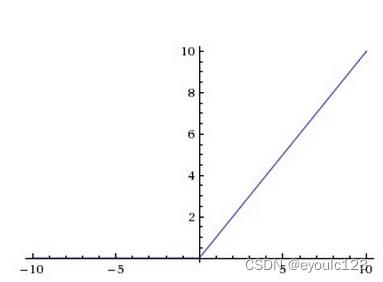
Sigmod函数:
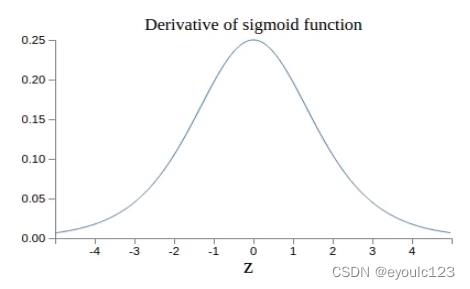
在上面的那个例子中,我们只有一个输入,就是房子的大小,即平米数。但是我们都知道房价并不只是与大小相关,还与位置、房型相关等其它因素相关。因此我们还需要将这些东西。我们假设位置为变量x1, 房型为x2参数,而每一种因素,我们都可以表示成一个类似于$y=bx +a$形式的方程,那么房价表示,可能就需要为:
总
房
价
=
(
房
屋
大
小
因
素
x
)
+
(
位
置
因
素
x
1
)
+
(
房
型
x
2
)
y
=
(
b
x
+
a
)
+
(
b
1
x
1
+
a
1
)
+
(
b
2
x
2
+
a
2
)
总房价 = (房屋大小因素x) + (位置因素 x1) + (房型 x2) \\\\ y = (bx + a) + (b_1x_1 +a_1) + (b_2x_2 + a_2)
总房价=(房屋大小因素x)+(位置因素x1)+(房型x2)y=(bx+a)+(b1x1+a1)+(b2x2 以上是关于人工智能介绍的主要内容,如果未能解决你的问题,请参考以下文章