相似矩阵过渡矩阵
Posted Zetaa
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了相似矩阵过渡矩阵相关的知识,希望对你有一定的参考价值。
申明: 仅个人小记
一、相似矩阵
P − 1 A P = B P^-1AP=B P−1AP=B
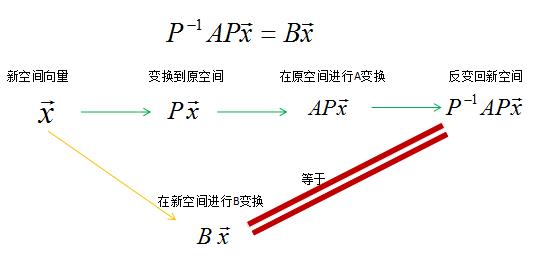
P − 1 A P x ⃗ = B x ⃗ P^-1AP\\vecx=B\\vecx P−1APx=Bx
x ⃗ \\vecx x是新空间的一个向量, P x ⃗ P\\vecx Px表示将新空间向量 x ⃗ \\vecx x变换为原空间向量, A P x ⃗ AP\\vecx APx是在原空间下做A变换, P − 1 A P x ⃗ P^-1AP\\vecx P−1APx是将变换结果反变回新空间, B x ⃗ B\\vecx Bx是在新空间下对向量 x ⃗ \\vecx x做B变换
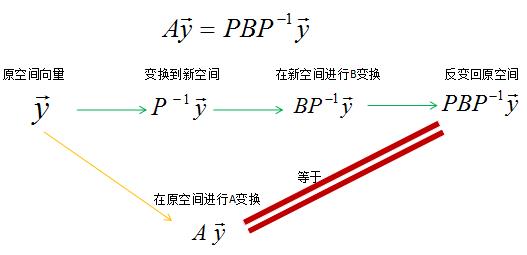
对上式进行变形,得 A = P B P − 1 A=PBP^-1 A=PBP−1
A
y
⃗
=
P
B
P
−
1
y
⃗
A\\vecy=PBP^-1\\vecy
Ay=PBP−1y
此时,
y
⃗
\\vecy
y是原空间的一个向量,
P
−
1
y
⃗
P^-1\\vecy
P−1y是将原空间向量
y
⃗
\\vecy
y变换到新空间,
B
P
−
1
y
⃗
BP^-1\\vecy
BP−1y则是在新空间中对向量
P
−
1
y
⃗
P^-1\\vecy
P−1y做B变换,
P
B
P
−
1
y
⃗
PBP^-1\\vecy
PBP−1y便是将变换结果
P
−
1
y
⃗
P^-1\\vecy
P−1y变换到原空间。
####二、过渡矩阵
R
3
R^3
R3空间的一个基
A
=
(
α
⃗
1
,
α
⃗
2
,
α
⃗
3
)
A=(\\vec \\alpha _1,\\vec \\alpha_2,\\vec \\alpha _3)
A=(α1,α2,α3),在取一个新基
B
=
(
β
⃗
1
,
β
⃗
2
,
β
⃗
3
)
B=(\\vec \\beta_1,\\vec \\beta_2,\\vec\\beta_3)
B=(β1,β2,β3),把矩阵
P
=
A
−
1
B
P=A^-1B
P=A−1B称为旧基A到新基B的过渡矩阵。
为什么这样称呼,看下式:
B
=
A
P
B=AP
B=AP
即对基A做变换P就可以得到基B。(为什么这样,我暂时不清楚,只当是选出一种作为规定吧)。
具体用处, x ⃗ = A − 1 B y ⃗ , 其 中 x ⃗ 是 基 A 下 的 坐 标 , y ⃗ 是 基 B 下 的 坐 标 \\vecx=A^-1B\\vecy, 其中\\vecx是基A下的坐标,\\vecy 是基B下的坐标 x=A−1By,其中x是基A下的坐标,y是基B下的坐