Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程
Posted LeonYiLeonYi
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程相关的知识，希望对你有一定的参考价值。
Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程
一、背景
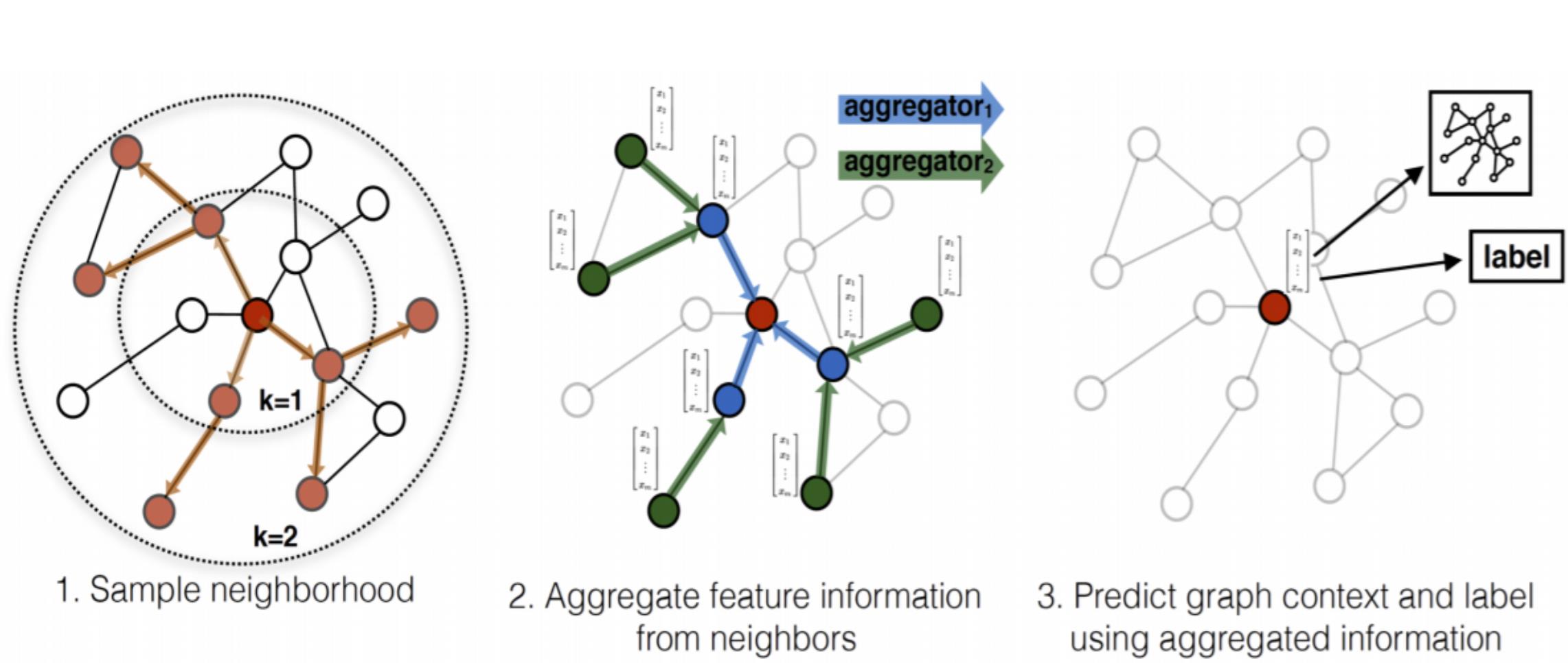
将卷积运算推广到不规则域通常表示为邻局聚合(neighborhood aggregation)或消息传递(neighborhood aggregation)模式。
x
i
(
k
−
1
)
∈
R
1
×
D
\\mathbfx^(k-1)_i \\in \\mathbbR^1 \\times D
xi(k−1)∈R1×D表示节点
i
i
i在第
(
k
−
1
)
(k-1)
(k−1)层的节点特征，
e
j
,
i
∈
R
1
×
F
\\mathbfe_j,i \\in \\mathbbR^1 \\times F
ej,i∈R1×F表示节点
j
j
j到节点的
i
i
i边特征（可选的），消息传递图神经网络可以描述为：
x
i
(
k
)
=
γ
(
k
)
(
x
i
(
k
−
1
)
,
□
j
∈
N
(
i
)
ϕ
(
k
)
(
x
i
(
k
−
1
)
,
x
j
(
k
−
1
)
,
e
j
,
i
)
)
,
\\mathbfx_i^(k) = \\gamma^(k) \\left( \\mathbfx_i^(k-1), \\square_j \\in \\mathcalN(i) \\, \\phi^(k)\\left(\\mathbfx_i^(k-1), \\mathbfx_j^(k-1),\\mathbfe_j,i\\right) \\right),
xi(k)=γ(k)(xi(k−1),□j∈N(i)ϕ(k)(xi(k−1),xj(k−1),ej,i)),
其中,
□
\\square
□表示可微且置换不变的聚合函数(aggregation function)，例如, sum、mean或max，消息函数(message function)
ϕ
\\phi
ϕ 和更新函数(update function)
γ
\\gamma
γ均为可微函数，例如MLP。
值得注意的是，一般GNN论文中通常给出的是聚合邻居信息的Aggregator和更新节点表示Updator，其Aggregator对应pytorch-geometric(PyG)中的消息函数和聚合函数。GNN本质上还是在做特征传播。
x
N
i
(
k
)
=
AGGREGATE
(
k
)
(
x
j
(
k
−
1
)
,
∀
j
∈
N
i
)
\\mathbfx_\\mathcalN_i^(k)=\\text AGGREGATE _(k)\\left(\\left\\\\mathbfx_j^(k-1), \\forall j \\in \\mathcalN_i\\right\\\\right)
xNi(k)= AGGREGATE (k)(xj(k−1),∀j∈Ni)
x
i
(
k
)
=
σ
(
W
(
k
)
⋅
[
x
i
(
k
−
1
)
∥
x
N
i
(
k
)
]
)
\\mathbfx_i^(k)=\\sigma\\left(\\mathbfW^(k) \\cdot\\left[\\mathbfx_i^(k-1) \\| \\mathbfx_\\mathcalN_i^(k)\\right]\\right)
xi(k)=σ(W(k)⋅[xi(k−1)∥xNi(k)])
例如，在GraphSage中，消息函数直接获取邻居节点 j ∈ N i j \\in \\mathcalN_i j∈Ni在第 k − 1 k-1 k−1层的嵌入，然后使用mean、max或LSTM作为聚合函数，更新函数将邻居中间嵌入和目标节点 i i i自身嵌入拼接后做线性变化。
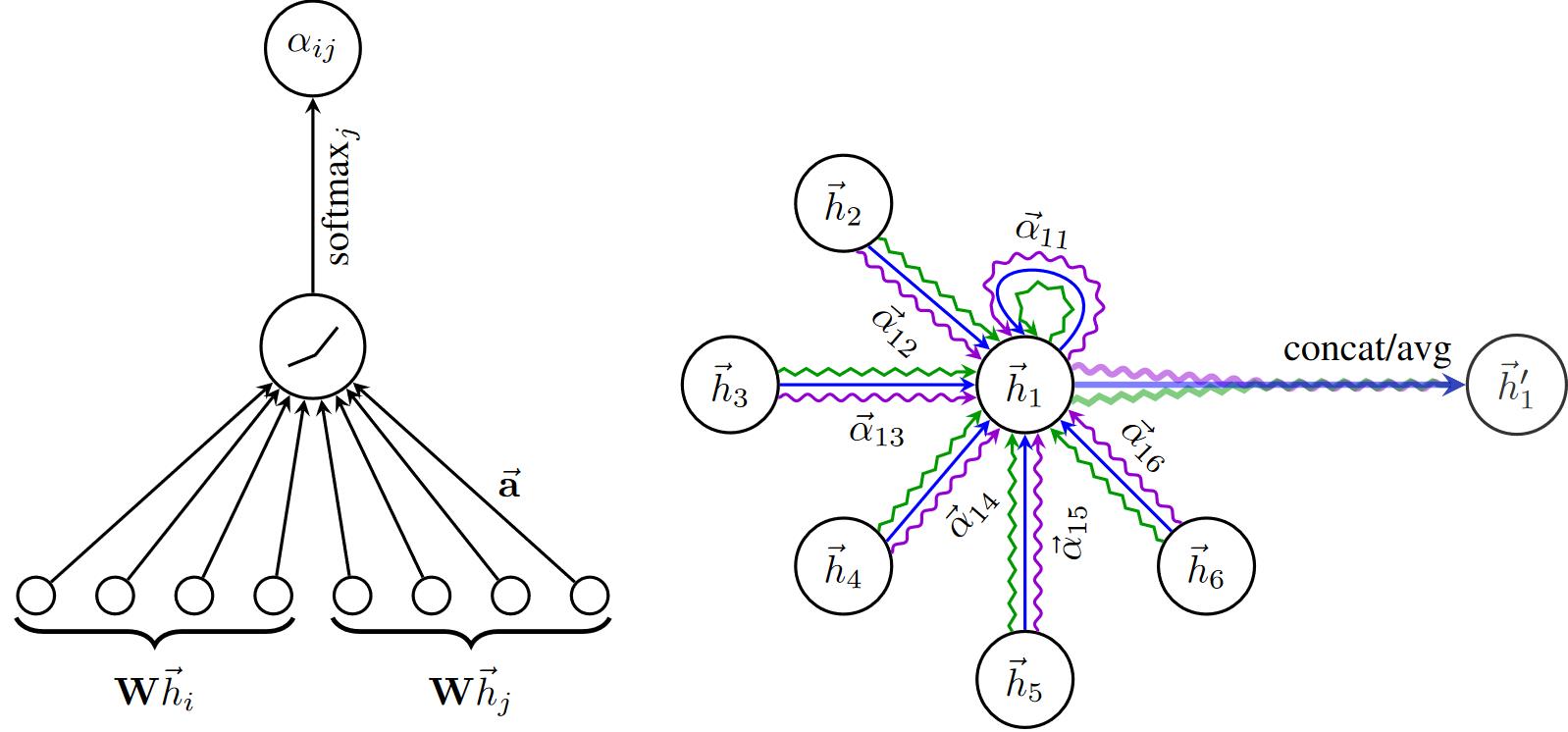
α
i
j
=
exp
(
Leaky ReLU
(
a
T
[
W
x
i
∥
W
x
j
]
)
)
∑
k
∈
N
i
exp
(
Leaky ReLU
(
a
T
[
W
x
i
∥
W
x
k
]
)
)
\\alpha_i j=\\frac\\exp \\left(\\text Leaky ReLU \\left(\\mathbfa^T\\left[\\mathbfW \\mathbfx_i \\| \\mathbfW \\mathbfx_j\\right]\\right)\\right)\\sum_k \\in \\mathcalN_i \\exp \\left(\\text Leaky ReLU \\left(\\mathbfa^T\\left[\\mathbfW \\mathbfx_i \\| \\mathbfW \\mathbfx_k\\right]\\right)\\right)
αij=∑k∈Niexp( Leaky ReLU (aT[Wxi∥Wxk]))exp( Leaky ReLU (aT[Wxi∥Wxj]))
x
i
′
=
∥
k
=
1
K
σ
(
∑
j
∈
N
i
α
i
j
k
W
k
x
j
)
\\mathbfx_i^\\prime=\\|_k=1^K \\sigma\\left(\\sum_j \\in \\mathcalN_i \\alpha_i j^k \\mathbfW^k \\mathbfx_j\\right)
xi′=∥k=1Kσ
j∈Ni∑αijkWkxj
又例如，在GAT中，消息函数根据注意力系数对节点嵌入进行归一化，然后使用"add"作为聚合函数。
二、MessagePassing基类
PyG的torch_geometric.nn中提供了MessagePassing基类，它通过自动处理消息传播来帮助创建此类消息传递图神经网络。用户只需重新定义
ϕ
\\phi
ϕmessage()和
γ
\\gamma
γupdate()及aggregation聚合方式（函数），例如aggr="add", aggr="mean" or aggr="max"，就可以实现自己GNN模型。
借助以下4个方法可实现上述目的：
MessagePassing(aggr="add", flow="source_to_target", node_dim=-2)：定义要使用的聚合方案（"add"，"mean"或"max"）和消息传递的流向（"source_to_target"或"target_to_source"）。 此外，node_dim属性指明沿哪个轴传播。
MessagePassing.propagate(edge_index, size=None, **kwargs): 开始传播消息的初始调用。它接收边索引edge_index和构造消息所需的所有其他数据，来更新节点嵌入。propagate()不仅可以在[N, N]的方矩中交换消息，还可通过传入size=(N, M)作为附加参数传递来交换形如[N, M]的稀疏分配矩阵（例如，推荐系统中的二部图）中的消息。如果size设为None，则矩阵为方阵。
MessagePassing.message(...)：类似
ϕ
\\phi
ϕ，构造每条边到节点
i
i
i的消息。若 flow="source_to_target"则
(
j
,
i
)
∈
E
(j,i) \\in \\mathcalE
(j,i)∈E和flow="target_to_source"则
(
i
,
j
)
∈
E
(i,j) \\in \\mathcalE
(i,j)∈E。它可接受最初传递给propagate()的任何参数。 此外，传递给propagate()的tensors可通过添加后缀_i和_j到变量名（例如，x_i和x_j）映射到对应的节点
i
i
i和
j
j
j。根据习惯，通常用
i
i
i表示聚合信息的中心节点（目标target），并用
j
j
Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程