人工智能原理自学高维空间：机器如何面对越来越复杂的问题

Posted 2023-01-21 文艺倾年

😊你好，我是小航，一个正在变秃、变强的文艺倾年。
🔔笔记来自B站UP主Ele实验室的《小白也能听懂的人工智能原理》。
🔔本文讲解高维空间：机器如何面对越来越复杂的问题，一起卷起来叭！

目录

• 一、“维度”
• 二、代码实现

一、“维度”

如果我们判断一个人是否会打篮球，仅仅通过身高角度显然是不合理的，我们还需要从其他角度分析，比如体重、身体灵活性以及是否经常见到凌晨四点钟的太阳等等因素。

同样在豆豆的世界，豆豆的毒性不仅与大小有关，还可能与颜色深浅、软硬等有关

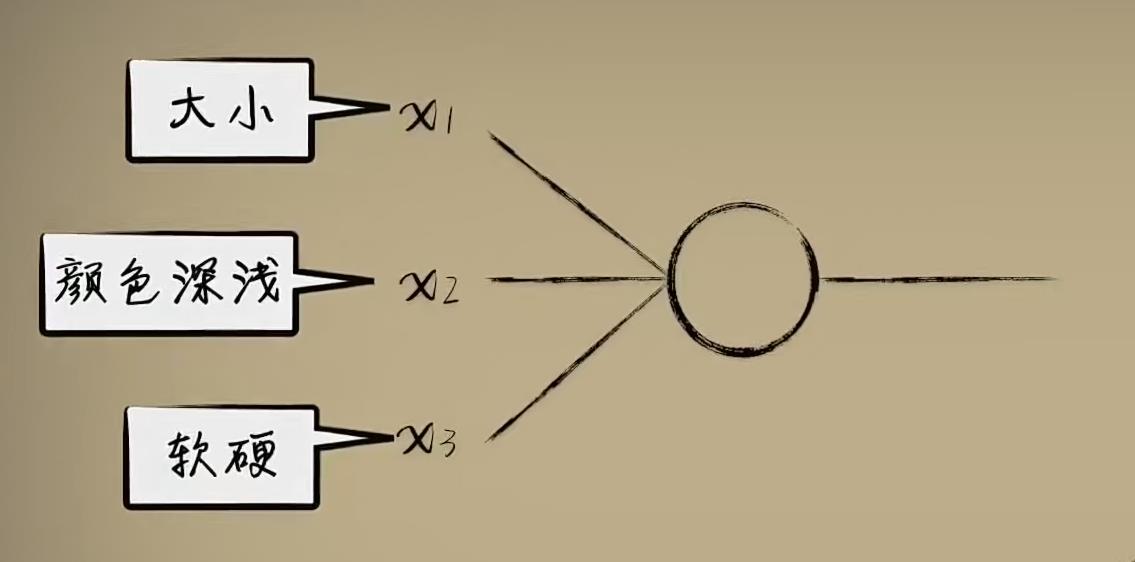
对于三维世界的我们，很难在四维空间作图，但是数学作为一种抽象的工具，在数学看来，这不过是在输入上增加了一个维度而已，输入数据有多少元素也就是所谓的特征维度，也叫数据维度。
也就是说我们从更多的维度观察豆豆的时候，也就能更好的预测它的毒性。

---

我们选择大小和颜色深浅两个维度为例：

此时预测函数的线性部分需要从一元一次函数变成二元一次函数


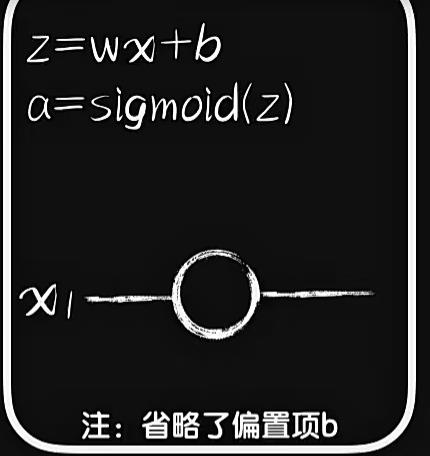
如果我们在三维坐标系中把这个函数画出来，很明显这是一个平面，正如一元一次函数中是一个线性函数

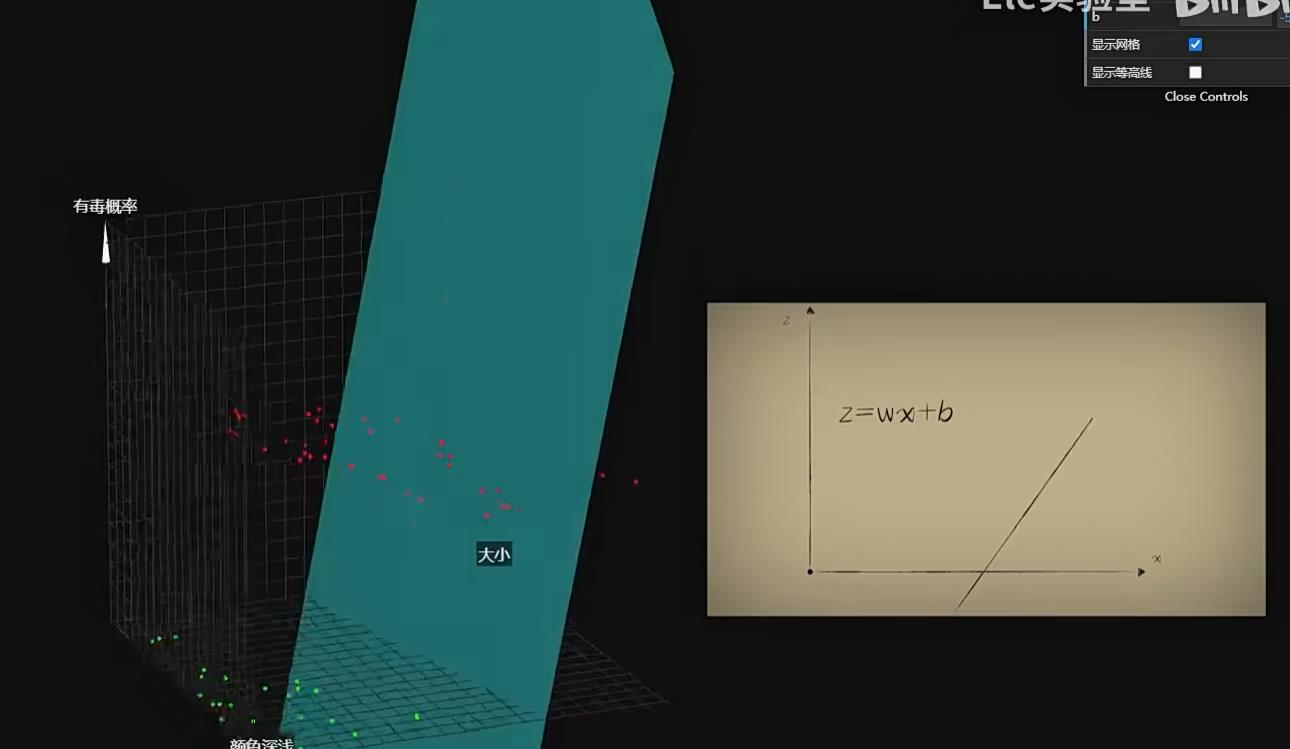
这个平面被非线性激活函数激活后，就被扭曲成了一个s型的曲面，正如一元一次函数的直线被激活函数激活后扭曲为一个s型曲线一样

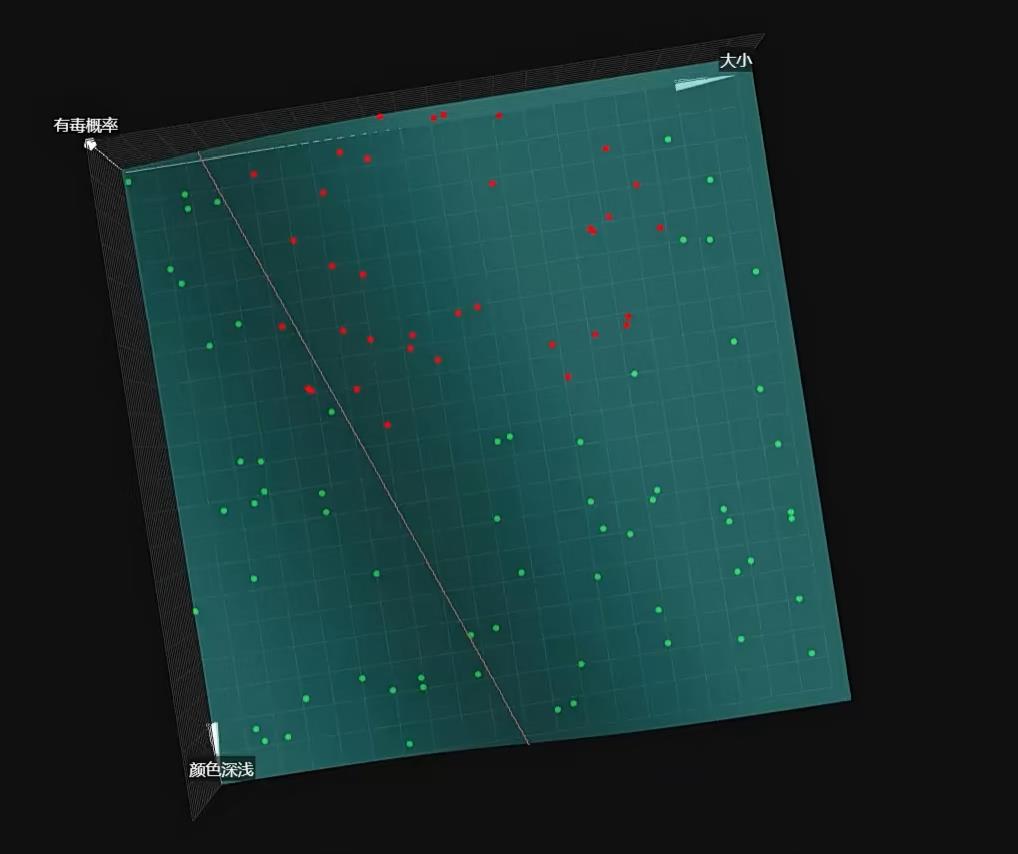
此时我们可以通过调节参数，在俯视下可以使用一条直线将豆豆分割为有毒无毒，而这条线也称为等高线、割线

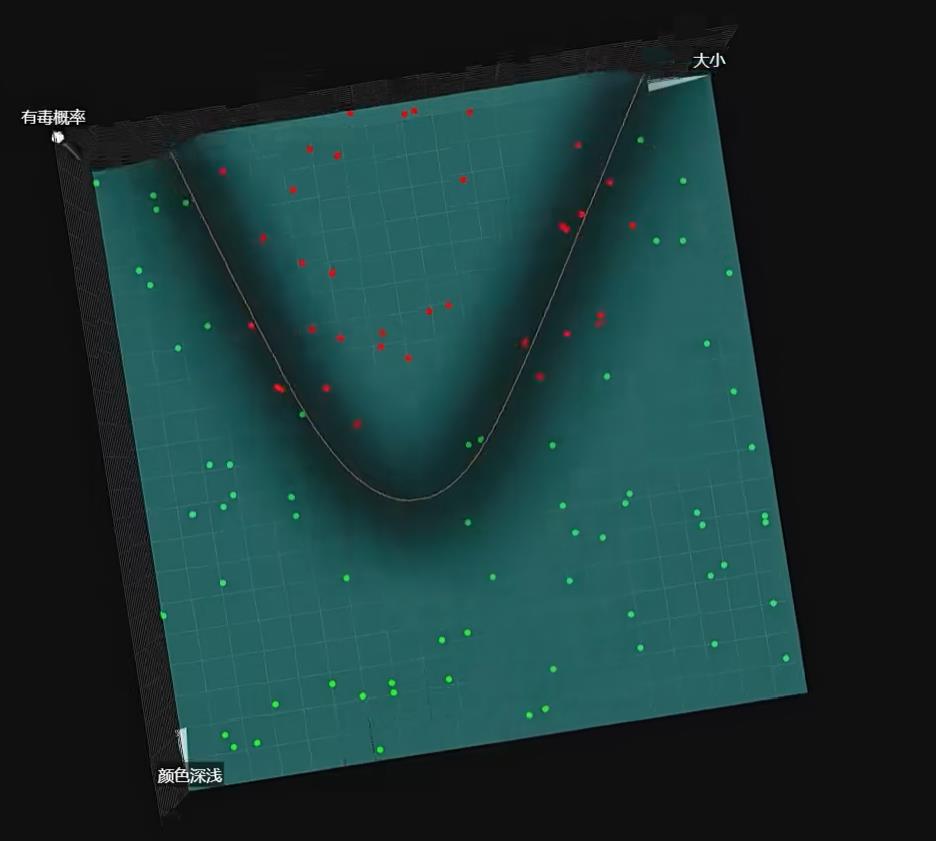
但如果豆豆的分布是这样的情况，我们上述的方法也就无能为力了，这种问题也被称为：线性不可分问题

这个时候我们就需要增加隐藏层神经元，让这个直线“弯曲”

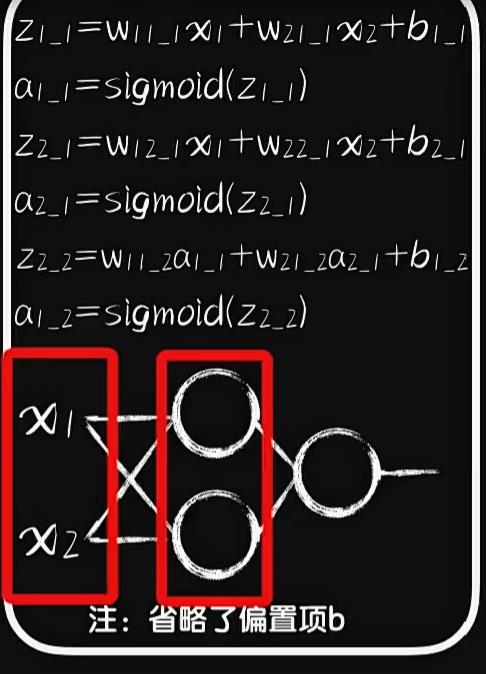
💡思考：需要几个隐藏神经元可以让分割线形成一个圈

二、代码实现

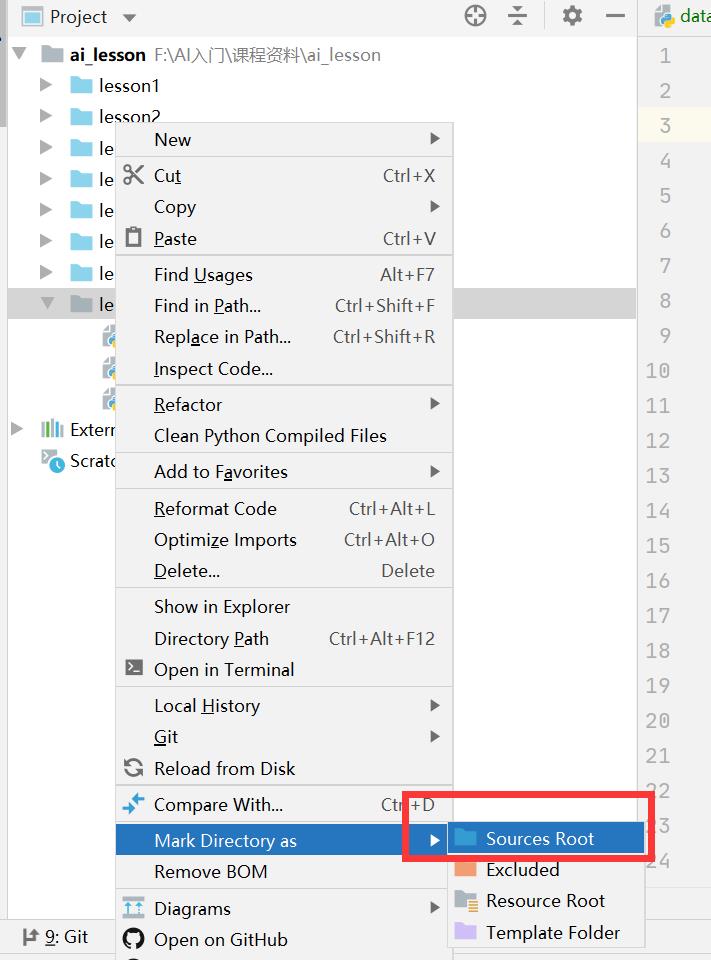
如遇到同包下引入.py文件爆红，右键将其加入到source root：
原因：目标文件不在pycharm编译path下

🔨豆豆数据集模拟：dataset.py

import numpy as np

def get_beans(counts):
	xs = np.random.rand(counts,2)*2
	ys = np.zeros(counts)
	for i in range(counts):
		x = xs[i]
		if (x[0]-0.5*x[1]-0.1)>0:
			ys[i] = 1
	return xs,ys

def get_beans2(counts):
	xs = np.random.rand(counts,2)*2
	ys = np.zeros(counts)
	for i in range(counts):
		x = xs[i]
		if (np.power(x[0]-1,2)+np.power(x[1]-0.3,2))<0.5:
			ys[i] = 1


	return xs,ys

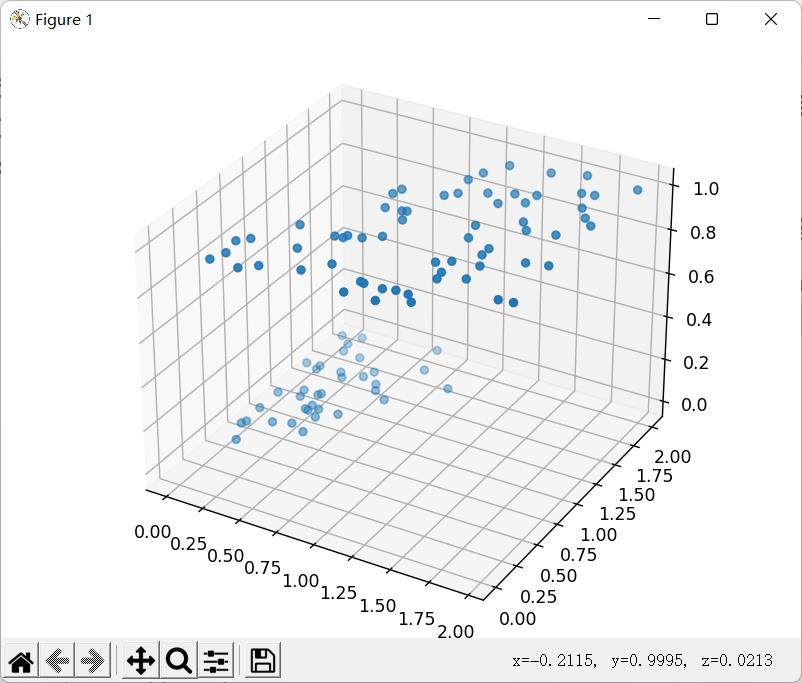
🚩豆豆毒性分布如下：

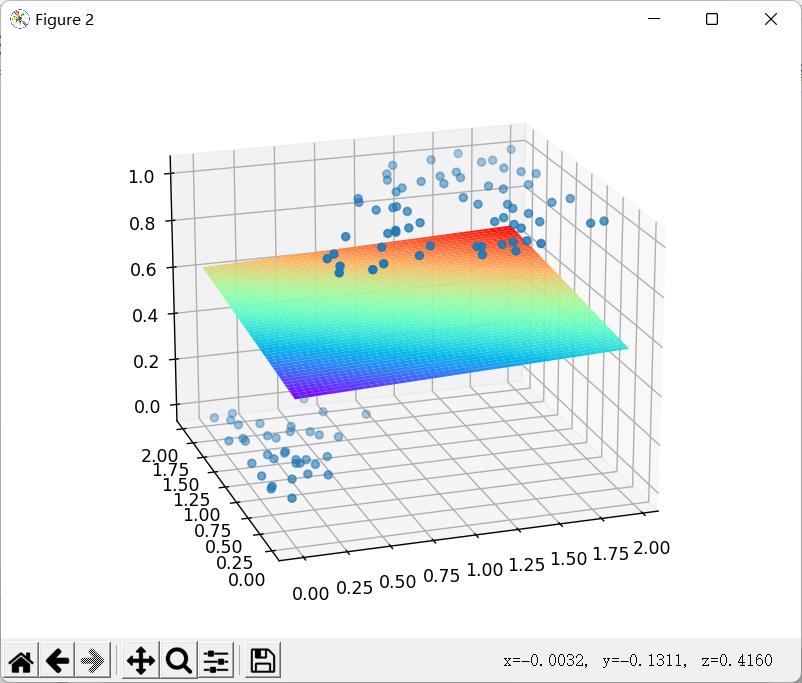
🚩梯度下降前：

🔨绘图工具封装：plot_utils.py

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

def show_scatter(xs,y):
	x = xs[:,0]
	z = xs[:,1]
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)
	plt.show()

def show_surface(x,z,forward_propgation):
	x = np.arange(np.min(x),np.max(x),0.1)
	z = np.arange(np.min(z),np.max(z),0.1)
	x,z = np.meshgrid(x,z)
	y = forward_propgation(x,z)
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()



def show_scatter_surface(xs,y,forward_propgation):
	x = xs[:,0]
	z = xs[:,1]
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)

	x = np.arange(np.min(x),np.max(x),0.01)
	z = np.arange(np.min(z),np.max(z),0.01)
	x,z = np.meshgrid(x,z)
	y = forward_propgation(x,z)
	
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()

🔨梯度下降：2_inputs_model.py

import numpy as np
import dataset
import plot_utils

m = 100
xs, ys = dataset.get_beans(m)
print(xs)
print(ys)

plot_utils.show_scatter(xs, ys)

w1 = 0.1
w2 = 0.2
b = 0.1

## [[a,b][c,d]]
## x1s[a,c]
## x2s[b,d]
## 逗号，区分的是维度，冒号：区分的是索引，省略号… 用来代替全索引长度
# 在所有的行上，把第0列切割下来形成一个新的数组
x1s = xs[:, 0]
x2s = xs[:, 1]

# 前端传播
def forward_propgation(x1s, x2s):
    z = w1 * x1s + w2 * x2s + b
    a = 1 / (1 + np.exp(-z))
    return a

plot_utils.show_scatter_surface(xs, ys, forward_propgation)

for _ in range(500):
    for i in range(m):
        x = xs[i] ## 豆豆特征
        y = ys[i] ## 豆豆是否有毒
        x1 = x[0]
        x2 = x[1]

        a = forward_propgation(x1, x2)

        e = (y - a) ** 2

        deda = -2 * (y - a)
        dadz = a * (1 - a)
        dzdw1 = x1
        dzdw2 = x2
        dzdb = 1

        dedw1 = deda * dadz * dzdw1
        dedw2 = deda * dadz * dzdw2
        dedb = deda * dadz * dzdb

        alpha = 0.01
        w1 = w1 - alpha * dedw1
        w2 = w2 - alpha * dedw2
        b = b - alpha * dedb

plot_utils.show_scatter_surface(xs, ys, forward_propgation)

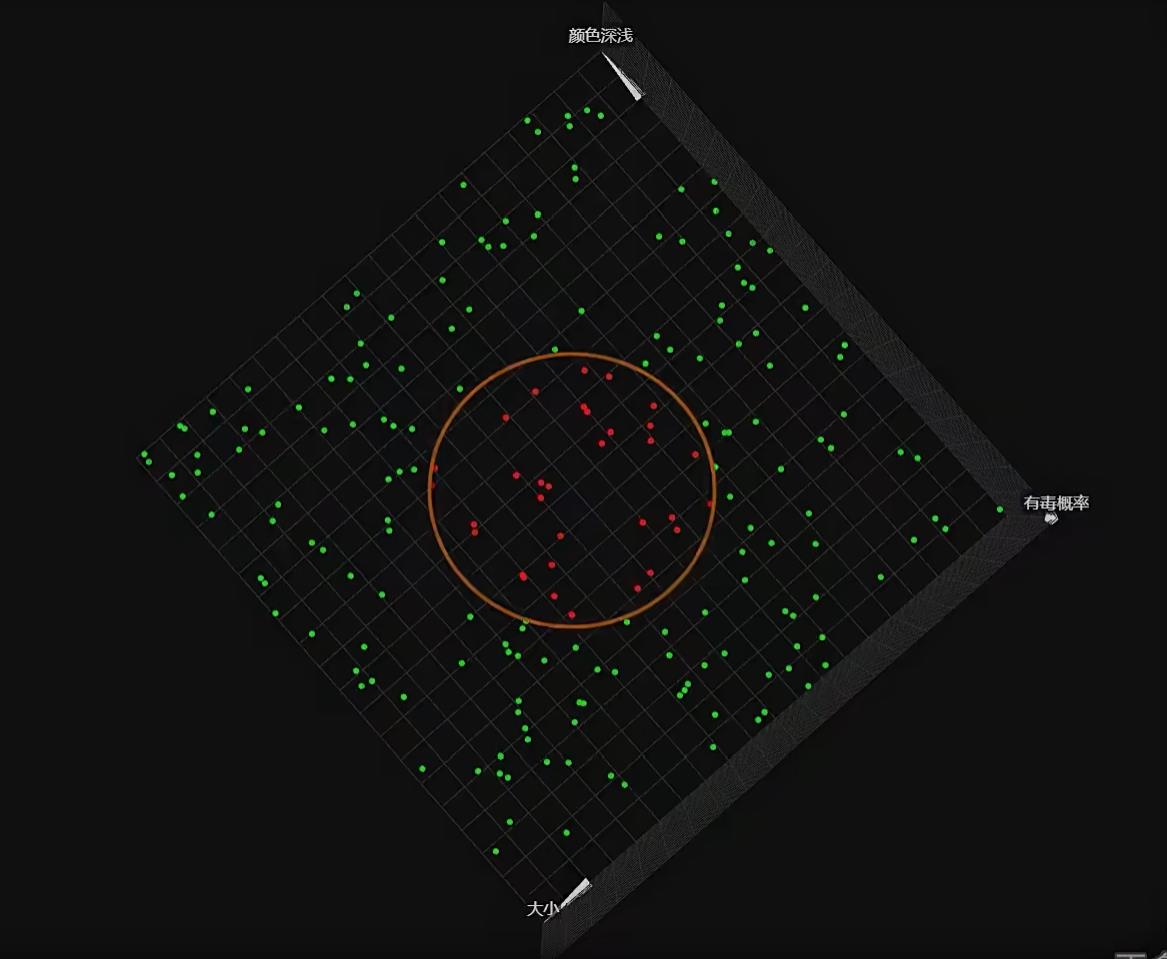
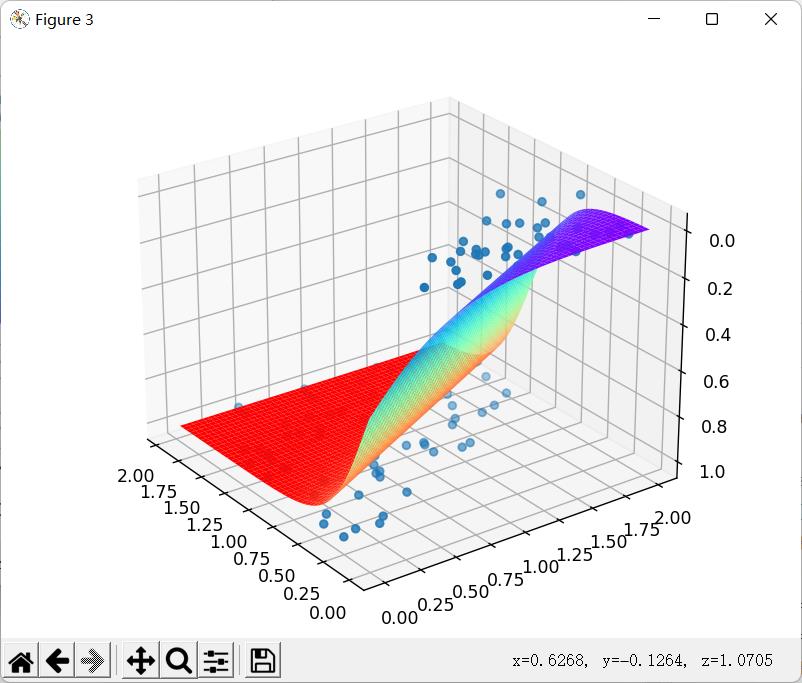
🚩梯度下降后：

📌 [ 笔者 ]   文艺倾年
📃 [ 更新 ]   2023.1.18
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！
🔍 [ 代码 ]   https://github.com/itxaiohanglover/ai_lesson