机器学习——一元线性回归

Posted 2023-01-19 ke

import numpy as np
import matplotlib.pyplot as plt

#加载数据集
data = np.genfromtxt("../data_linear.csv",delimiter=",")
x_data = data[:,0]
y_data = data[:,1]

# #展示数据集
# plt.scatter(x_data,y_data)
# plt.show()

#设置基本参数
lr = 0.001
k = 0
b = 0
epochs = 50#最大迭代次数

#最小二乘法
def compute_error(b,k,x_data,y_data):
    totalError = 0
    for i in range(0,len(x_data)):
        totalError += (y_data[i]-(k*x_data[i]+b))**2
    return totalError / float(len(x_data))/2

def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
    m = float(len(x_data))#计算总数据量
    for i in range(epochs):#循环50次
        b_grad = 0
        k_grad = 0
        for j in range(0,len(x_data)):#计算梯度总和再求和
            b_grad +=(1/m)*((k*x_data[j]+b)-y_data[j])
            k_grad +=(1/m)*(x_data[j])*(((k*x_data[j]+b)-y_data[j]))
        b = b-(lr*b_grad)
        k = k-(lr*k_grad)
    return b,k


print(f"Starting b = b, k = k, error = compute_error(b,k,x_data,y_data)")
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print(f"After epochs iterations b = b, k = k, error = compute_error(b,k,x_data,y_data)")

# 画图
plt.plot(x_data, y_data, 'b.')  # "b是蓝色 .表示用点表示"
plt.plot(x_data, k * x_data + b, 'r')
plt.show()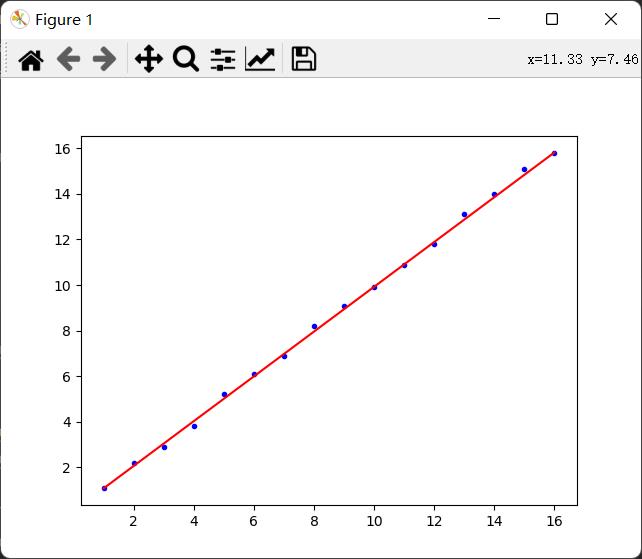

利用sklearn

from sklearn.linear_model import LinearRegression
import numpy as np
from matplotlib import pyplot as plt

data = np.genfromtxt("../data_linear.csv",delimiter=",")

x_data = data[:,0,np.newaxis]# 构建特征x：第0列   一维变为二维-->np.newaxis
y_data = data[:,1,np.newaxis]
# plt.scatter(x_data, y_data)
# plt.show()
#创建拟合模型
model = LinearRegression()
#训练模型
model.fit(x_data,y_data)
#画图
plt.plot(x_data,y_data,'b .')
plt.plot(x_data,model.predict(x_data),'r')
plt.show()