bingc++(mapset树哈希位图布隆过滤器)
Posted 月屯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了bingc++(mapset树哈希位图布隆过滤器)相关的知识,希望对你有一定的参考价值。
目录标题
前言
底层为红黑树结构C++98二叉搜索树+平衡限制
- map: K-V–键值对—key必须唯一
- set: K—key必须唯一
- multimap: K-V–键伯对—key是可以重复
- multiset K----key是可以重复
底层为哈希结构:C++11
都足关于key有序的,并且查找的时间复杂度都是O(IogN)
map
map[]运算符重载做法

map中的顺序
默认按key升序,如果key一致,按照升序
multimap
基本使用
#include <iostream>
using namespace std;
#include <map>
#include <string>
int main()
multimap<string, string> m;
m.insert(pair<string, string>("orange", "橙子"));
m.insert(make_pair("pear", "梨"));
m.insert(make_pair("banana", "香蕉"));
m.insert(make_pair("apple", "苹果"));
m.insert(make_pair("orange", "橘子"));
cout << m.size() << endl;
cout << m.count("orange") << endl;
m.erase("orange");
if (m.find("orange") != m.end())
cout << "删除了一个" << endl;
else
cout << "删除所有key为orange的键值对" << endl;
for (auto& e : m)
cout << e.first << "--->" << e.second << endl;
cout << endl;
return 0;
set
树
二叉搜索树
平衡二叉树
红黑树
-
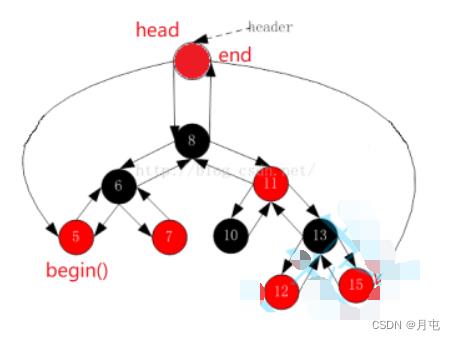
红黑树的性质
1.每个结点不是红色就是黑色
2.根节点是黑色的
3如果一个节点是红色的,则它的两个孩子结点是黑色的每条路径中黑色节点个数相同(不会出现连在一起的红色节点)
4.对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5.每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点 -
情况一: cur为红,p为红,g为黑,u存在且为红
解决:p、u调黑,g调红
1.如果g是根节点,调整完成后,需要将g改为黑色
2.如果g是子树,g一定有双亲,且g的双亲如果是红色,把g当成cur,需要继续向上调整,否则结束 -
情况二: cur为红(p左孩子),p为红,g为黑,1.u不存在(cur新插入)/2.u为黑(cur不是新插入)
u是黑色时,为什么现在cur是红色的?
因为:新节点一定是插入到cur的子树中,导致子树违反了红黑树形式在调整的过程当中,将cur由黑色改成了红色才出现现在所看到的场景
cur和p其中一个节点的颜色一定要设置成黑色注意: cur肯定不能设置为黑色
因为:如果叔叔节点存在并且为黑色时,cur之前的颜色一定是黑色的,往上调整的时候好不容易将cur由黑色改成红色,cur及其子树满足红黑树的性质,现在如果将cur直接改成黑色,则会导致cur子树不满足红黑树的性质
想法:只能将p设置为黑色
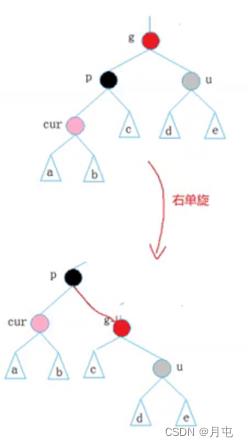
解决方案:
将双亲和祖父节点的颜色交换对g子树进行右单旋处理
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红
- 情况三: cur为红(p右孩子),p为红,g为黑,u不存在/u为黑
解决方案:变成情况二
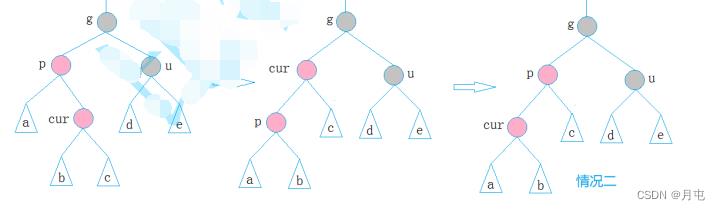
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
map、set应用
哈希
哈希冲突
简单分析哈希函数设计是否合理
注意:
a.哈希函数的值域必须在表格的范围之内
b.哈希函数计算出的结果尽可能均匀
c.哈希函数设计尽可能简单
- 直接定制法–(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B 优点:简单、均匀 缺点:需要事先
知道关键字的分布情况 使用场景:适合查找比较小且连续的情况
字符 - 除留余数法–(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址 - 平方取中法–(了解)
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址; 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况 - 折叠法–(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况 - 随机数法–(了解)
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。通常应用于关键字长度不等时采用此法 - 数学分析法–(了解)
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。例如:
假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是 相同的,那么我们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改 成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀的情况
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
闭散列
线性探测
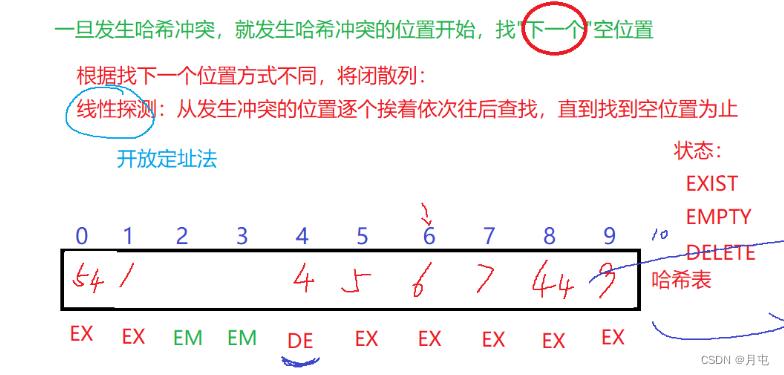
线性探测优点:解决冲突的方式简单
线性探测缺陷:容易产生数据的堆积(一旦产生冲突,冲突的元素容易连城一片)
合布负载因子:有效元素个数/表格容量
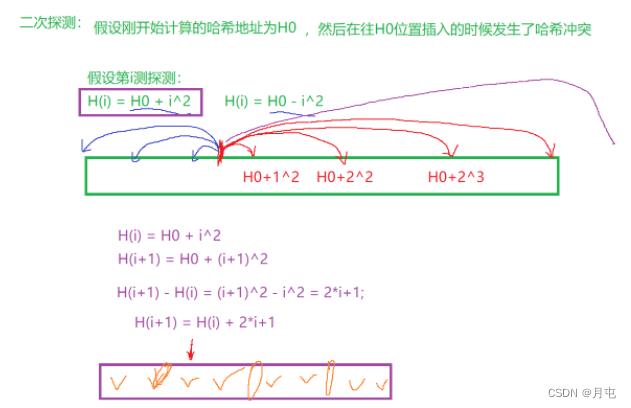
二次探测
开散列
开散列的应用-- unordermap、unorderset
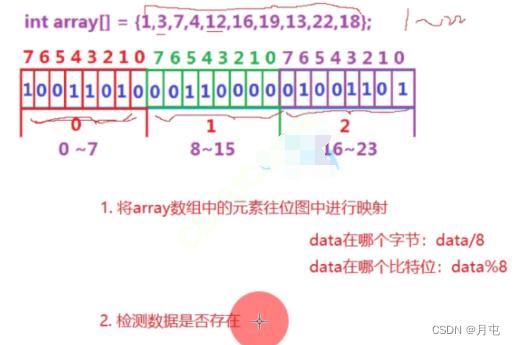
位图
#include <iostream>
using namespace std;
#include <bitset>
int main()
int array[] = 1, 3, 7, 4, 12, 16, 19, 13, 22, 18 ;
// 先要预算总共需要多少个比特位
bitset<23> bs;
// 将数组中的元素映射到位图中
for (auto e : array)
bs.set(e);
cout << bs.count() << endl;
cout << bs.size() << endl;
if (bs.test(13))
cout << "13 is in array" << endl;
else
cout << "13 is not in array" << endl;
bs.reset(13);
if (bs.test(13))
cout << "13 is in array" << endl;
else
cout << "13 is not in array" << endl;
cout << bs.to_string() << endl;
cout << bs.to_ulong() << endl;
bitset<32> bs1(0x55555555);
cout << bs1.to_string() << endl;
return 0;
位图的应用
- 快速查找某个数据是否在一个集合中
- 排序
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
布隆过滤器
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
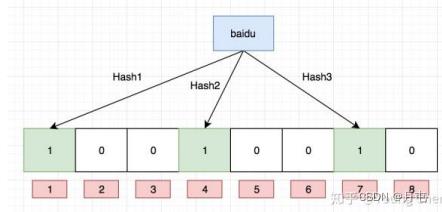
源码模拟
布隆过滤器优点
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 哈希函数相互之间没有关系,方便硬件并行运算
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白
名单,存储可能会误判的数据) - 不能获取元素本身
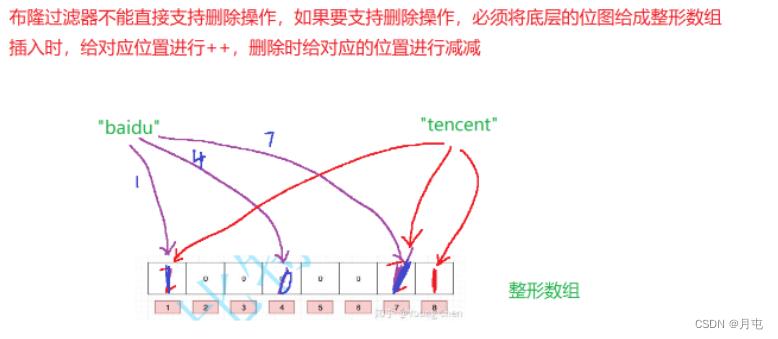
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
常见面试题
以上是关于bingc++(mapset树哈希位图布隆过滤器)的主要内容,如果未能解决你的问题,请参考以下文章