傅里叶伯德图的简单示例

Posted 2023-01-15 王张飞

试例1

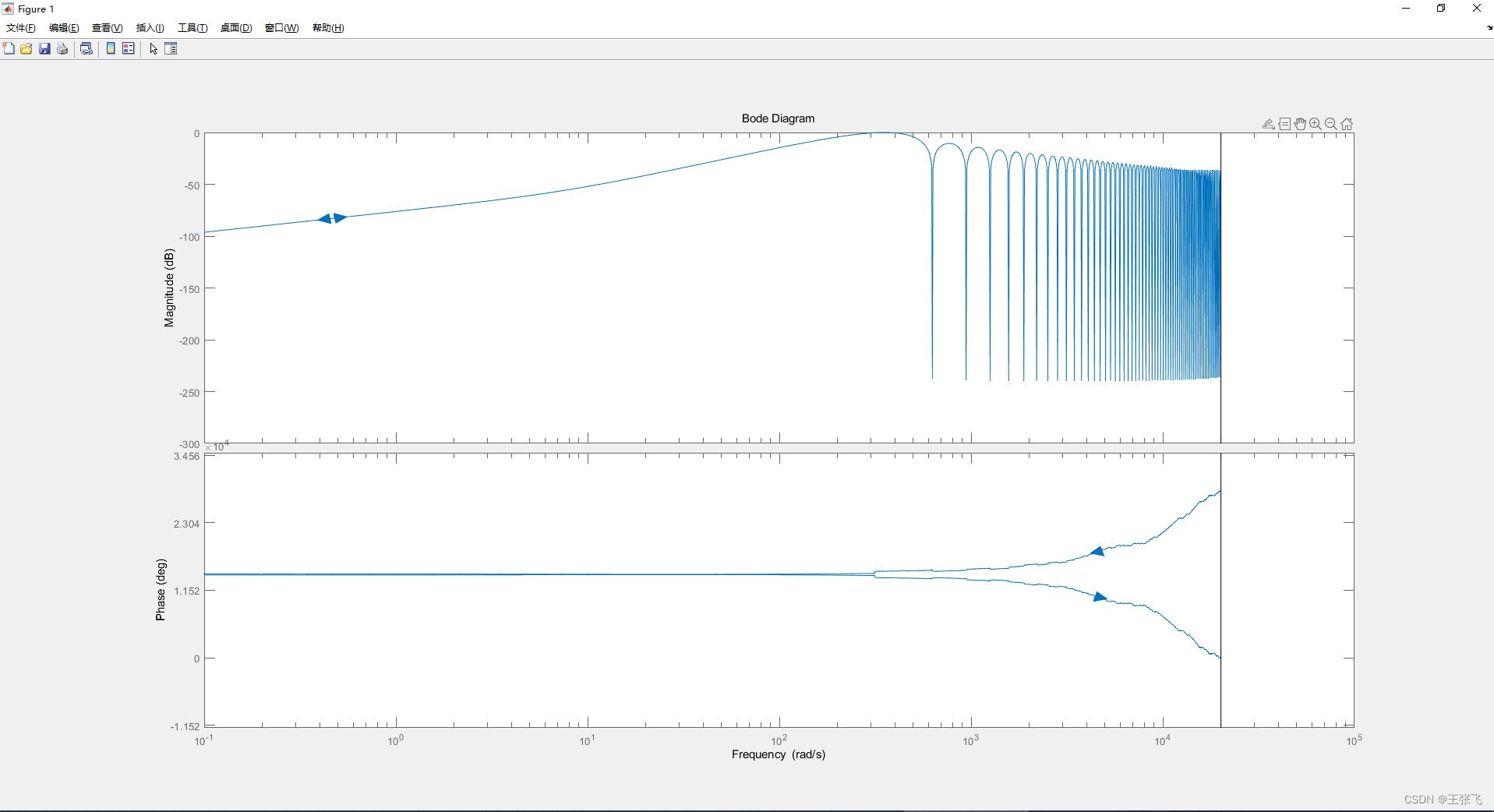
%% 连续性图
N=128;
ts=1/(N*50);
H1=tf([1 zeros(1,N-1) -1],[N -N*exp(1i*2*pi/N) zeros(1,N-1)],ts);
H2=tf([1 zeros(1,N-1) -1],[N -N*exp(-1i*2*pi/N) zeros(1,N-1)],ts);
H3=parallel(H1,H2);

bode(H3)

试例2

%% 离散化图
% 2017 zhao  3/5 jie gaosi wavelet filter
clear, close all
sys1=tf([-2 3.6 -32 1.7],[1 3.3 16.8 25.4 40 13 ]);
sys2=tf([-2 3.6],[1 3.3 16.8 25.4]);
sys1
sys2
interval=100;%w的另一种定义：频率限制在1e-2-1e+3之间，整个图像用interval个点来画
w = logspace(-2, 3, interval);
% ********************************************************************
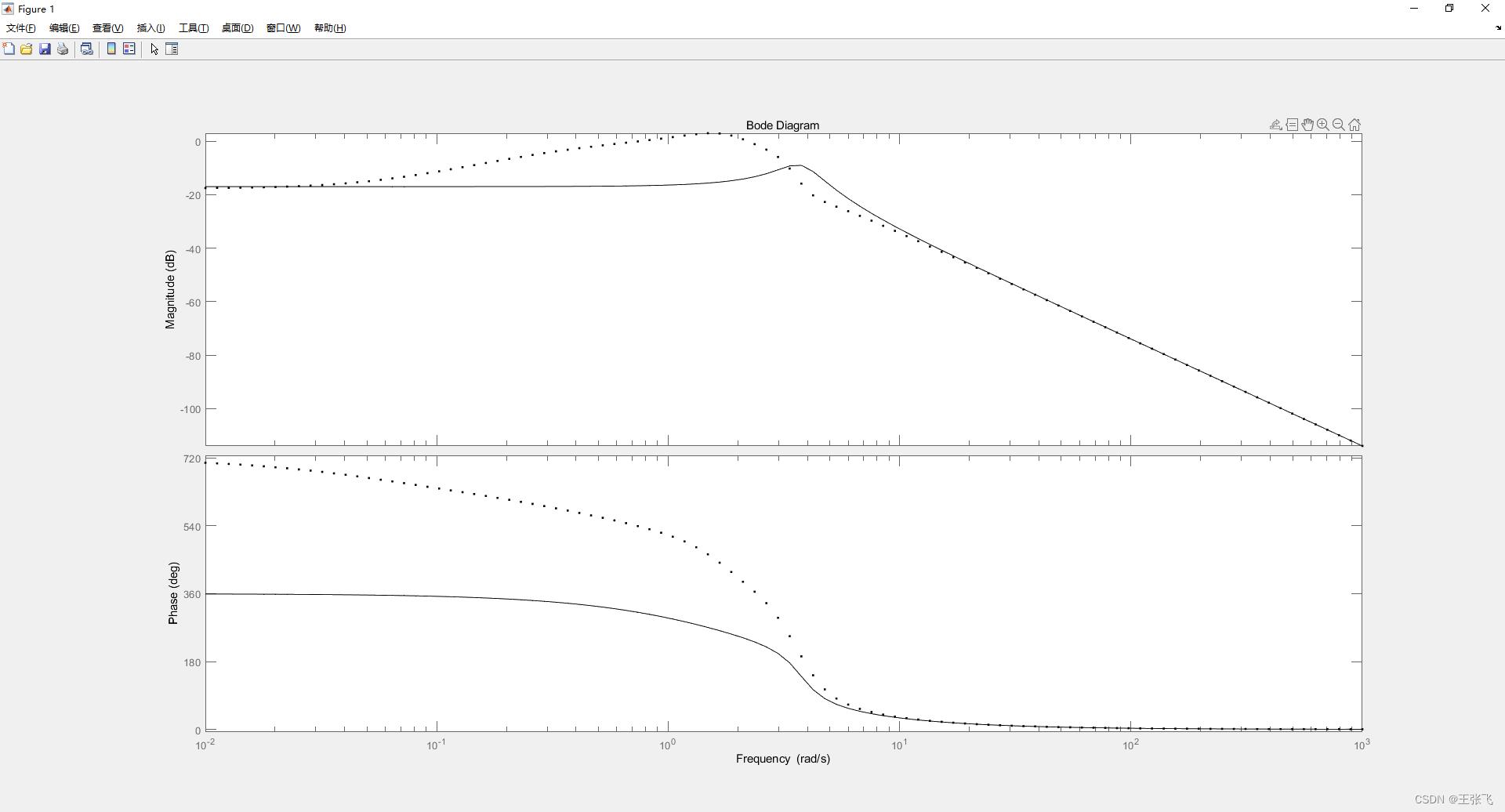
figure(1)
bode(sys1,'k.',sys2,'k-',w)%画多个伯德图
% ********************************************************************
w=0.01,100%w的一种定义：频率限制在0.01-100
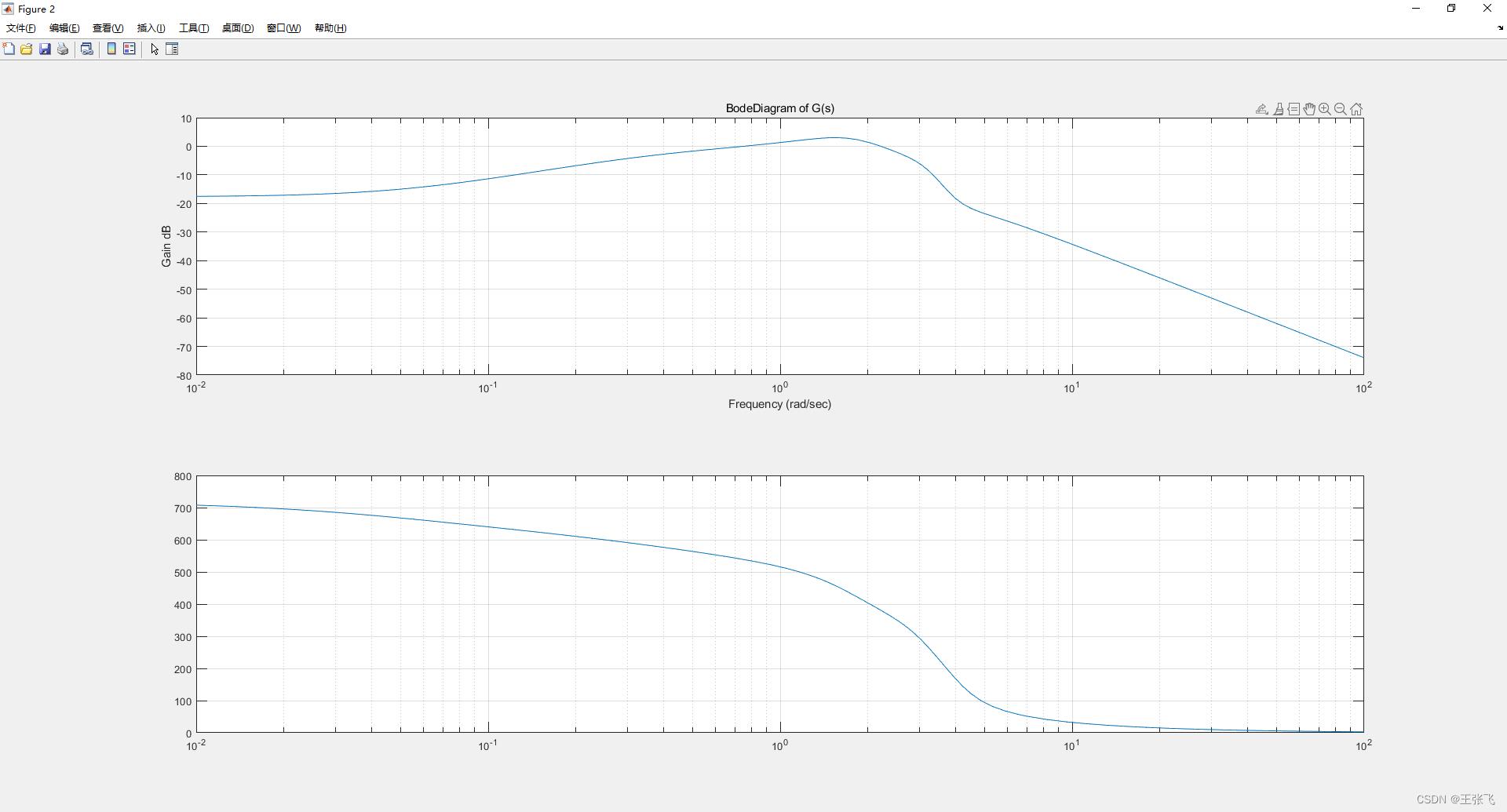
figure(2)
num =[-2 3.6 -32 1.7];
den = [1 3.3 16.8 25.4 40 13 ];
[mag, phase, w] = bode(num, den, w);%用bode(sys1），会将mag转化为数组，导致无法画图
magdB = 20*log10(mag);%输出的为hz，转化为rad/s
% dBmax = 5*ones(1,interval); %画一下横线，可以实现控制上下限的效果
% dBmin = -50*ones(1,interval); %点数必须与 w 中频率点的数目相等
subplot(2, 1, 1)
% semilogx(w, magdB, '.', w, dBmax, 'r-', w, dBmin, 'r:')
semilogx(w, magdB, '-')
grid
title('BodeDiagram of G(s)')
xlabel('Frequency (rad/sec)')
ylabel('Gain dB')
subplot(2, 1, 2)
% pmax = 150*ones(1,interval); 
% pmin = -150*ones(1,interval);
% semilogx( w, phase, '.', w, pmax, '--', w, pmin, ':')
semilogx( w, phase, '-')
grid%画格子

试例3

%% 多项式和零极点转换
Gain=2;
Z=[3;4];
P=[1;4;7];

po=zpk(Z,P,Gain)
%执行该语句后建立了系统的零-极点形式模型
tfr=tf(po)
%执行该命令后得到了多项式形式传递函数模型

[num,den]=zp2tf(Z,P,Gain)
% 执行该命令后得到了多项式传递函数的分子、分母系数

[Z1,P1,K1] =tf2zp(num,den)
% 执行该命令后得到了系统的零-极点形式系数

Results：

>> WANGSUOECU

po =
 
    2 (s-3) (s-4)
  -----------------
  (s-1) (s-4) (s-7)
 
Continuous-time zero/pole/gain model.


tfr =
 
     2 s^2 - 14 s + 24
  ------------------------
  s^3 - 12 s^2 + 39 s - 28
 
Continuous-time transfer function.

num =
     0     2   -14    24
den =
     1   -12    39   -28
Z1 =
     4
     3
P1 =
    7.0000
    4.0000
    1.0000
K1 =
     2
>> 

试例4

%% 零极点分布图
clc%清空命令行
clear%从工作区中删除项目、释放系统内存
clf%清空当前图窗窗口
num=[1];
den=[1 2 2 1];
sys=tf(num,den);%构成传递函数
poles=roots(den);%求极点
subplot(211);%图1
pzmap(sys);%零极点分布图显示
[r,p,k]=residue(num,den)%实现部分分式展开的
t=0:0.02:10;
h1=impulse(num,den,t);%单位冲击响应
subplot(222)
plot(t,h1,'linewidth',4)
title('冲击响应','fontsize',16)
xlabel('时间\\t','fontsize',16)
h2=step(num,den,t);%单位阶跃响应
subplot(223)
plot(t,h2,'linewidth',4)
title('阶跃响应','fontsize',16)
xlabel('时间\\t','fontsize',16)
[H,w]=freqs(num,den);
subplot(224)
plot(w,abs(H),'linewidth',4)
xlabel('频率\\omega','fontsize',16)
title('幅频特性','fontsize',16)
ylabel('幅值H(jw)','fontsize',16)

Results：

r =
   1.0000 + 0.0000i
  -0.5000 - 0.2887i
  -0.5000 + 0.2887i
p =
  -1.0000 + 0.0000i
  -0.5000 + 0.8660i
  -0.5000 - 0.8660i
k =
     []
警告: 更新 Text 时出错。

 字符串标量或字符向量必须具备有效的解释器语法:
时间\\t
 
警告: 更新 Text 时出错。

 字符串标量或字符向量必须具备有效的解释器语法:
时间\\t
 
>>