227. 基本计算器 II
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了227. 基本计算器 II相关的知识,希望对你有一定的参考价值。
227. 基本计算器 II
题目
传送门:https://leetcode.cn/problems/basic-calculator-ii/submissions/

算法设计:栈
一个功能完备的计算器功能,有很多功能,我们需要从最简单的功能迭代起来。
先宏观,再微分:
- 输入:字符串,需要把字符串转为数字
- 功能:加减、乘除优先、括号优优先
- 细节:读到空格跳过、不溢出整型最大值
计算的关键在于优先级处理,括号 > 乘除 > 加减。
第一步,字符串转整数。
int str_to_int( string s ) // 字符串转整数
int num = 0;
for( int i=0; str.length(); i++ )
if( isdigit(str[i]) ) // 输入字符串为数字
num = 10 * num + (c - '0');
第二步,实现加减。
- 核心思路是把字符串分解成符号和数字的组合,如 2 - 3,变成 +2、-3。
int calculate(string s)
stack<int> stk; // 记录算式中的数字
int num = 0; // 保存字符串转数字后的数字
char sign = '+'; // 记录每个数字之前的运算符,因为第一个数字没有符号的(3-2),设置为符号+(+3-2),如果第一个数是负数,那就是 +0
for (int i = 0; i < s.size(); i++) // 遍历字符串
if (isdigit(s[i])) // 读到数字
num = 10 * num + (s[i] - '0'); // "123" -> 100 + 20 + 3 -> 123
if ( (!isdigit(c) && c != ' ') || i == s.size() - 1 ) // s[i]是符号且不是空格(运算符) or 最后一个字符之后没有符号可读取了,所以也要入栈直接计算
switch (sign) // 看数字前的 sign 来决定怎么处理 s[i] 前面的数
case '+':
stk.push(num); break; // 加法将之前的数字入栈
case '-':
stk.push(-num); break; // 加法将之前数字的相反数入栈
sign = s[i]; // 更新符号为当前符号
// 把 3-2 代入分析,初始sign为+,遍历到s[0]把'3'->3,再遍历s[1]到'-',后遍历到s[2]让+3入栈,更新sign为'-'。
num = 0; // 数字清零,计算下一个数字
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty())
res += stk.top();
stk.pop();
return res;
第三步,实现乘除。
- 核心思路依然是把字符串分解成符号和数字的组合,如 1*4,如 +1、*4。
乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈。
class Solution
public:
int calculate(string s)
stack<int> stk;
int num = 0;
char sign = '+';
for (int i = 0; i < s.size(); i++)
if (isdigit(s[i]))
num = 10 * num + (s[i] - '0');
if ( (!isdigit(s[i]) && s[i] != ' ') || i == s.size() - 1 )
switch (sign)
int pre;
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
case '*':
pre = stk.top(); // 只要拿出前一个数字做对应运算即可
stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top(); // 只要拿出前一个数字做对应运算即可
stk.pop();
stk.push(pre / num);
break;
sign = s[i];
num = 0;
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty())
res += stk.top();
stk.pop();
return res;
;
第四步,处理括号。
括号具有递归性质。
calc(3 * (4 - 5/2) - 6)
= 3 * calc(4 - 5/2) - 6
= 3 * 2 - 6
= 0
无论多少层括号嵌套,通过 calc 函数递归调用自己,都可以将括号中的算式化简成一个数字。
括号包含的算式,直接视为一个数字就可。
- 遇到
(开始递归 - 遇到
)结束递归
class Solution:
def calculate(self, s: str) -> int:
def calc(s: List) -> int:
stack = []
sign = '+'
num = 0
while len(s) > 0:
c = s.popleft()
if c.isdigit():
num = 10 * num + int(c)
# 遇到左括号开始递归计算 num
if c == '(':
num = calc(s)
if (not c.isdigit() and c != ' ') or len(s) == 0:
if sign == '+':
stack.append(num)
elif sign == '-':
stack.append(-num)
elif sign == '*':
stack[-1] = stack[-1] * num
elif sign == '/':
# python 除法向 0 取整的写法
stack[-1] = int(stack[-1] / float(num))
num = 0
sign = c
# 遇到右括号返回递归结果
if c == ')': break
return sum(stack)
return calc(collections.deque(s))
你看,加了两三行代码,就可以处理括号了。
C++ 完整代码:
class Solution
public:
int calculate(string str)
int index = 0;
return calc(str, index);
int calc(string &s, int &index)
stack<int> tokens;
int num = 0;
char sign = '+';
for (; index < s.size() + 1; ++index)
char c = s[index];
if (isdigit(c))
num = num * 10 + (c - '0');
if (c == '(')
index++;
num = calc(s, index);
continue;
if (!isdigit(c) && c != ' ')
int temp;
switch (sign)
case '+':
tokens.push(num);
break;
case '-':
tokens.push(-num);
break;
case '*':
temp = tokens.top();
tokens.pop();
tokens.push(temp * num);
break;
default:
temp = tokens.top();
tokens.pop();
tokens.push(temp / num);
num = 0;
sign = c;
if (c == ')')
break;
int result = 0;
while (!tokens.empty())
result += tokens.top();
tokens.pop();
return result;
;
至此,计算器的全部功能就实现了,通过对问题的层层拆解化整为零。
扩展:后缀表达式
计算思路:先把中缀表达式转化为后缀表达式,所有符号都在运算数字后面出现,可以不用括号了。
- 中缀表达式:9 + (3-1) * 3 + 10 / 2
- 后缀表达式:9 3 1 - 3 * + 10 2 / +
再从左到右遍历后缀表达式,遇到数字就进栈,遇到符号就将处于栈顶俩个数字出栈运算,运算结果入栈,一直重复,就可以计算出最终结果。
那怎么把中缀表达式转化为后缀表达式?
从左到右遍历中缀表达式的每个数字和符号,若是数字就加入后缀表达式。
引入一个栈存储符号:
- 若是左括号,入栈
- 若是右括号则一直出栈直到左括号出栈为止,出栈后加入后缀表达式
- 若此符号优先级高于栈顶符号(乘除 > 加减),入栈
- 若此符号优先级低于栈顶符号(加减 < 乘除),则栈顶元素全部出栈并加入后缀表达式,并将当前符号进栈
- 一直到最终的后缀表达式
举例,遍历中缀表达式 9 + (3-1) * 3 + 10 / 2。
第 1 个字符是数字 9,加入后缀表达式
- 后缀表达式:9
第二个字符是符号 +,入栈
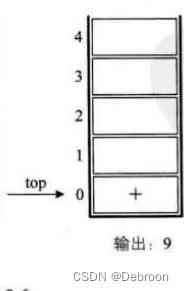
第三个字符是符号 ‘(’,因为是左括号还没配对,入栈。
第四个字符是数字 3,加入后缀表达式
- 后缀表达式:9 3
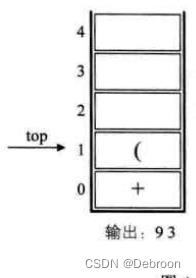
第五个字符 ‘-’,入栈。
第六个数字 1,加入后缀表达式。

第七个字符 ‘)’,若是右括号则一直出栈直到左括号出栈为止,出栈后加入后缀表达式。
- 后缀表达式:9 3 1 -
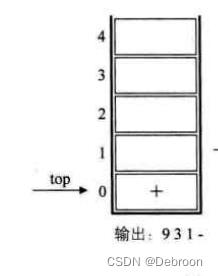
第八个数字 3,加入后缀表达式。
- 后缀表达式:9 3 1 - 3
第九个符号 ‘*’,栈顶元素是 ‘+’,此符号大于栈顶元素,入栈。
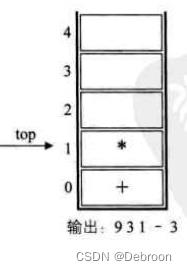
第十个字符 ‘+’,栈顶元素是 ‘*’,此符号小于栈顶元素,栈中元素全部出栈(没有比 + 号更低的优先级,所以全部出栈),并加入后缀表达式,并将当前符号进栈。
- 后缀表达式:9 3 1 - 3 * +
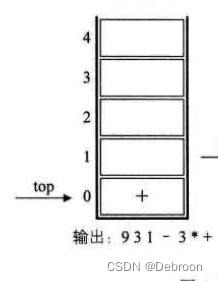
第十一个数字 10,加入后缀表达式
- 后缀表达式:9 3 1 - 3 * + 10
第十二个字符 ‘/’,栈顶元素是 ‘+’,若此符号优先级高于栈顶符号(乘除 > 加减),入栈

第十三个数字 2,加入后缀表达式
- 后缀表达式:9 3 1 - 3 * + 10 2
因为是字符串的最后一个字符,所以栈中全部字符全部出栈并加入后缀表达式
- 后缀表达式:9 3 1 - 3 * + 10 2 / +
以上是关于227. 基本计算器 II的主要内容,如果未能解决你的问题,请参考以下文章