从零开始学习深度学习35. 门控循环神经网络之门控循环单元（gated recurrent unit，GRU）介绍Pytorch实现GRU并进行训练预测
Posted 阿_旭
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了从零开始学习深度学习35. 门控循环神经网络之门控循环单元（gated recurrent unit，GRU）介绍Pytorch实现GRU并进行训练预测相关的知识，希望对你有一定的参考价值。
在循环神经网络中，当时间步数较大或者时间步较小时，循环神经网络的梯度较容易出现衰减或爆炸。上一篇文章中介绍的裁剪梯度可以应对梯度爆炸，但无法解决梯度衰减的问题。因此，循环神经网络在实际中较难捕捉时间序列中时间步距离较大的依赖关系。
为了更好地捕捉时间序列中时间步距离较大的依赖关系，从而提出了门控循环神经网络（gated recurrent neural network）。它可以通过学习的门来控制信息的流动。其中，门控循环单元（gated recurrent unit，GRU）是一种常用的门控循环神经网络 。
目录
1. 门控循环单元设计
门控循环单元的设计在原始RNN的基础上引入了重置门（reset gate）和更新门（update gate）的概念，从而修改了循环神经网络中隐藏状态的计算方式。
1.1 重置门和更新门
如下图所示，门控循环单元中的重置门和更新门的输入均为当前时间步输入 X t \\boldsymbolX_t Xt与上一时间步隐藏状态 H t − 1 \\boldsymbolH_t-1 Ht−1，输出由激活函数为sigmoid函数的全连接层计算得到。
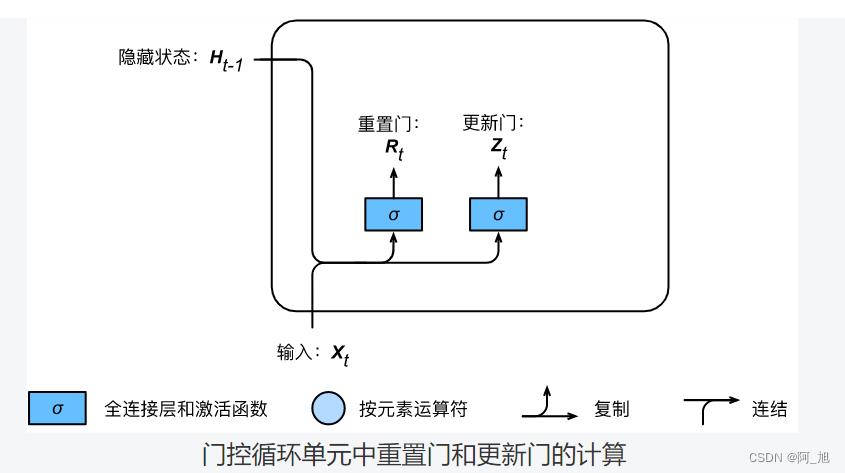
假设隐藏单元个数为 h h h，给定时间步 t t t的小批量输入 X t ∈ R n × d \\boldsymbolX_t \\in \\mathbbR^n \\times d Xt∈Rn×d（样本数为 n n n，输入个数为 d d d）和上一时间步隐藏状态 H t − 1 ∈ R n × h \\boldsymbolH_t-1 \\in \\mathbbR^n \\times h Ht−1∈Rn×h。重置门 R t ∈ R n × h \\boldsymbolR_t \\in \\mathbbR^n \\times h Rt∈Rn×h和更新门 Z t ∈ R n × h \\boldsymbolZ_t \\in \\mathbbR^n \\times h Zt∈Rn×h的计算如下：
R t = σ ( X t W x r + H t − 1 W h r + b r ) , Z t = σ ( X t W x z + H t − 1 W h z + b z ) , \\beginaligned \\boldsymbolR_t = \\sigma(\\boldsymbolX_t \\boldsymbolW_xr + \\boldsymbolH_t-1 \\boldsymbolW_hr + \\boldsymbolb_r),\\\\ \\boldsymbolZ_t = \\sigma(\\boldsymbolX_t \\boldsymbolW_xz + \\boldsymbolH_t-1 \\boldsymbolW_hz + \\boldsymbolb_z), \\endaligned Rt=σ(XtWxr+Ht−1Whr+br),Zt=σ(XtWxz+Ht−1Whz+bz),
其中 W x r , W x z ∈ R d × h \\boldsymbolW_xr, \\boldsymbolW_xz \\in \\mathbbR^d \\times h Wxr,Wxz∈Rd×h和 W h r , W h z ∈ R h × h \\boldsymbolW_hr, \\boldsymbolW_hz \\in \\mathbbR^h \\times h Whr,Whz∈Rh×h是权重参数， b r , b z ∈ R 1 × h \\boldsymbolb_r, \\boldsymbolb_z \\in \\mathbbR^1 \\times h br,bz∈R1×h是偏差参数。sigmoid函数可以将元素的值变换到0和1之间。因此，重置门 R t \\boldsymbolR_t Rt和更新门 Z t \\boldsymbolZ_t Zt中每个元素的值域都是 [ 0 , 1 ] [0, 1] [0,1]。
1.2 候选隐藏状态
接下来，门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。如下图所示，我们将当前时间步重置门的输出与上一时间步隐藏状态做按元素乘法（符号为
⊙
\\odot
⊙）。如果重置门中元素值接近0，那么意味着重置对应隐藏状态元素为0，即丢弃上一时间步的隐藏状态。如果元素值接近1，那么表示保留上一时间步的隐藏状态。然后，将按元素乘法的结果与当前时间步的输入连结，再通过含激活函数tanh的全连接层计算出候选隐藏状态，其所有元素的值域为
[
−
1
,
1
]
[-1, 1]
[−1,1]。
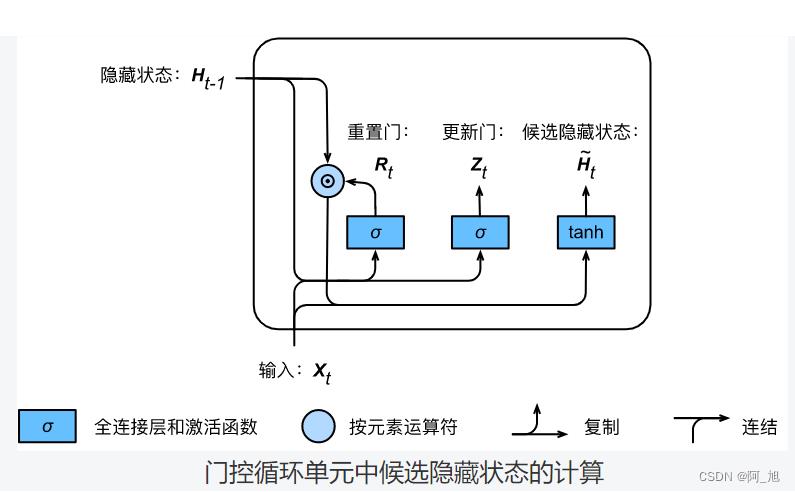
具体来说，时间步 t t t的候选隐藏状态 H ~ t ∈ R n × h \\tilde\\boldsymbolH_t \\in \\mathbbR^n \\times h H~t∈Rn×h的计算为
H ~ t = tanh ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h ) , \\tilde\\boldsymbolH_t = \\texttanh(\\boldsymbolX_t \\boldsymbolW_xh + \\left(\\boldsymbolR_t \\odot \\boldsymbolH_t-1\\right) \\boldsymbolW_hh + \\boldsymbolb_h), H~t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh),
其中 W x h ∈ R d × h \\boldsymbolW_xh \\in \\mathbbR^d \\times h Wxh∈Rd×h和 W h h ∈ R h × h \\boldsymbolW_hh \\in \\mathbbR^h \\times h Whh∈Rh×h是权重参数， b h ∈ R 1 × h \\boldsymbolb_h \\in \\mathbbR^1 \\times h bh∈R1×h是偏差参数。从上面这个公式可以看出，重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。而上一时间步的隐藏状态可能包含了时间序列截至上一时间步的全部历史信息。因此，重置门可以用来丢弃与预测无关的历史信息。
1.3 隐藏状态
最后，时间步 t t t的隐藏状态 H t ∈ R n × h \\boldsymbolH_t \\in \\mathbbR^n \\times h Ht∈Rn×h的计算使用当前时间步的更新门 Z t \\boldsymbolZ_t Zt来对上一时间步的隐藏状态 H t − 1 \\boldsymbolH_t-1 Ht−1和当前时间步的候选隐藏状态 H ~ t \\tilde\\boldsymbolH_t H~t做组合：
门控循环单元 GRU 动手学深度学习v2
深度学习与图神经网络核心技术实践应用高级研修班-Day2循环神经网络（RNN）