K-D Tree原理和应用
Posted QtHalcon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了K-D Tree原理和应用相关的知识,希望对你有一定的参考价值。
kd 树(k-dimensional tree)是一个包含空间信息的二项树数据结构,它是用来计算 kNN 的一个非常常用的工具。如果特征的维度是 D,样本的数量是N,那么一般来讲 kd 树算法的复杂度是O(D log(N)),相比于穷算的 O(DN) 省去了非常多的计算量。
1 构建KD树
k-d-tree是一棵每个节点都为k维点的二叉树,其中所有非叶子节点可以视作用一个超平面把空间分区成两个半空间( Half-space )。因为有很多种方法可以选择轴垂直分区面( axis-aligned splitting planes ),所以有很多种创建k-d-tree的方法。最典型的方法如下:
-
选择维度:KD树建树采用的是从m个样本的n维特征中,分别计算n个特征的值的方差,用方差最大的第k维特征 来作为根节点。
-
选择中位数:对于这个特征,我们选择特征的取值的中位数 v对应的样本作为划分点
-
分割数据:对于所有第k维特征的取值小于 v的样本,我们划入左子树,对于第k维特征的取值大于等于 v的样本,我们划入右子树。
-
递归迭代:对于左子树和右子树,我们采用和刚才同样的办法来找方差最大的特征来做更节点,将空间和数据集进一步细分,如此直到所有点都被划分。
下面举个例子,对如下数据点进行构建KD树

构建KD树的具体步骤为:
-
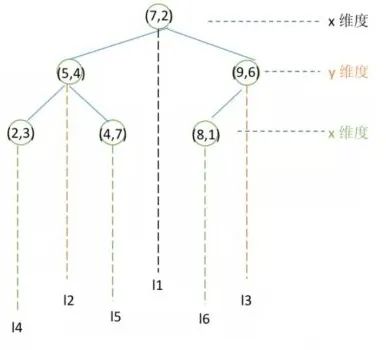
确定分割维度:6个数据点在x,y维度上的数据方差分别为39,28.63,在x轴上方差更大,所以分割维度为x。
-
确定分割数据点:根据x维上的值将数据排序,6个数据的中值(即中间大小的值)为7,所以分割数据点为(7,2)。这样,该节点的分割超平面就是直线x=7。
-
左子树空间和右子树空间分别递归
分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点=(2,3),(5,4),(4,7);另一部分为右子空间,包含2个节点=(9,6),(8,1);然后左右子空间分别重复进行上述过程。
2 最近邻搜索
k-d-tree的最典型应用就是最近邻搜索,它在数据搜索、kNN中具有重大意义。
最邻近搜索用来找出在树中与目标点最接近的点,k-d树最邻近搜索的算法原理如下:
-
从根节点开始,递归地往下移。如果目标点在分区面的左边则进入左子节点,在右边则进入右子节点,并对走过的节点进行标记;
-
在接近叶节点前,如果往左或往右下移时出现没有子节点的情况,则强制进入到另一侧的子节点,保证必须最终到达的是叶节点;一旦移动到叶节点,将该节点当作"当前最邻近点"。
-
根据之前走过的节点记录,从叶节点逆向回溯,并对每个经过的节点递归地执行下列步骤:
1)如果目前所在节点比"当前最邻近点"更靠近输入点,则将其变为当前最邻近点,其距离为最近距离。
2)检查目前所在节点的子树有没有更近的点,如果有则从该节点往下找。更具体地说,(要不要搜索某一边的子树需要)检查当前的分割超平面与“目标点为球心,以目标点与“当前最邻近点”间距离为半径的超球体”是否相交。
a)如果相交,可能在该子树对应区域内存在距离目标点更近的点,按照前面的1.2步骤移动到该子树,直到其叶子节点;
b)如果不相交,向上回退。
-
当回退到根节点时,搜索结束。最后的“当前最邻近点"即为最近邻点。
下面距离说明最近邻搜索的工作过程。如下图所示,目标点即图中的绿色query points。现在我们要找到k-d-tree中离这个目标点最近的点。
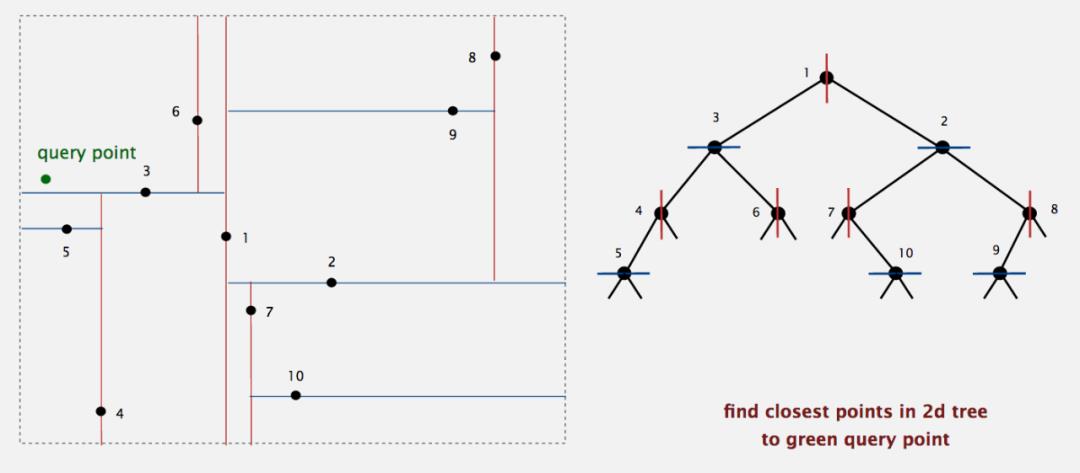
按照算法描述的规则,首先从根节点开始搜索,因为目标点位于由点1确定的超平面的左侧,所以进入左子节点。接下来,因为目标点位于点3的上方,所以进入点3的右子节点。由于点6是叶节点,所以将该节点当作"当前最邻近点"(如果此时没有6节点(空节点),则强制进入对侧节点(点4),然后直到找到叶节点),并计算其与目标点的距离,作为最小距离。
然后,回溯查找。经过节点3,计算目标到点3的距离,发现目前所在点3比"当前最邻近点"6更靠近目标点,则将3变为当前最邻近点。此时需要考虑要不要进入到3点的另一侧子树。

由于想讨论节点3的左子树中是否有更佳的最近邻,而节点3的左子树对应的区域是节点3所确定的分割超平面的下方。所以就是要看以目标点为中心,以目标点到点3的距离为半径的球(或者圆)是否与节点3所确定的分割超平面的下方区域有交叉。所以根据算法描述,我们检查由3确定分割超平面与“目标点x为球心,以目标点x与“当前最邻近点”3之间距离为半径的超球体”是否相交。显然相交,所以需要搜索节点3的左子树。

节点3的左子树由上图中右侧的蓝色三角标识出。对于现在经过的节点4,计算点x到点4的距离,显然大于当前距离,所以无需更新"当前最邻近点"。但我们还要考虑是否继续搜寻节点4的左右子树。于是我们检查由4确定分割超平面与“目标点x为球心,以目标点x与“当前最邻近点”3之间距离为半径的超球体”是否相交。显然相交,所以需要搜索节点4的左右子树(非回溯过程)。但是其右子树为空,可不考虑。
对于节点4的左子树,计算从点5到目标点x的距离,发现比之前的(从3到x的)距离短,所以将5更新为"当前最邻近点"。
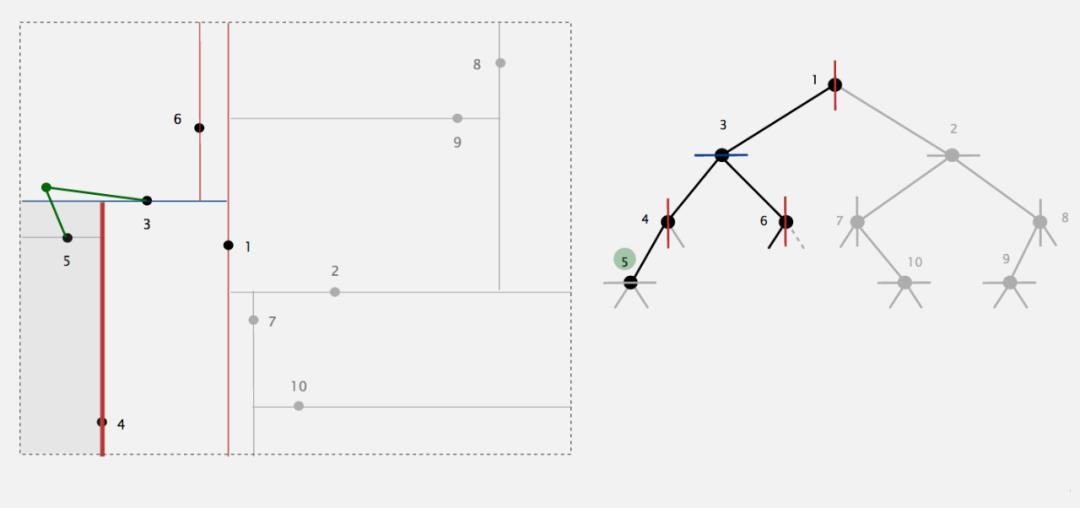
然后算法回退到节点4,到节点3,节点3的左右子树及其本身都已考察过,继续回退到节点1。对于节点1,其左子树已经考察完毕,我们考虑是否要检测它的右子树。检查由1确定分割超平面与“目标点x为球心,以目标点与“当前最邻近点”5之间距离为半径的超球体”是否相交。显然不相交,所以不需要搜索节点1的右子树。最后计算从点1到目标点x的距离,发现不比之前的(从5到x的)距离短,所以不更新最邻近点。因为已经回退到根节点,搜索结束。最后的“当前最邻近点"5即为x的最近邻点。
3 区域范围搜索
区域(范围)搜索的主要目的在于找出所有位于给定区域(最好是规则图形:矩形、圆形等,便于检测点是否在其里)中的点。主要通过执行如下三个步骤来实现:
从根节点开始,先判断根节点是否在给定区域中;
-
如果根节点完全在给定区域的左侧/下侧(根据分区维度判断),则以根节点的右子树递归;
-
如果根节点完全在给定区域的右侧/上侧(根据分区维度判断),则以根节点的左子树递归;
-
如果根节点骑跨在给定区域内(根据分区维度判断),则以根节点的左、右子树递归;
来看下面这个例子。从根节点开始,先检查点1是否在矩形框里,答案是不在。于是继续检查它的子树。因为矩形框位于点1的左侧(也就是说框中的点在x轴方向上要小于点1),于是继续搜索其左子树,而直接忽略其右子树。
接下来检查点3(也就是点1的孩子节点),答案是不在。于是继续(递归地)检查它的子树。但是因为矩形框横跨由过点3的超平面所划分的上下两个子空间,所以要继续搜索它的左右两个子树。
如此递归地搜索下去,最后就会发现点5位于矩形框中。

标准情况下,Range Search的时间复杂度是R+logN,其中R是要返回的点的数量,N是空间中点的总数。最糟糕的情况下,Range Search的时间复杂度是R+sqrt(N)。
4 PLC例子
以下案例通过两种方式进行邻域搜索,方式一是指定搜索最近的K个邻居,方式二是通过指定半径搜索邻居
#include <pcl/point_cloud.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <iostream>
#include <vector>
#include <ctime>
//#include <pcl/search/kdtree.h>
//#include <pcl/search/impl/search.hpp>
#include <pcl/visualization/cloud_viewer.h>
int
main(int argc, char **argv)
// 用系统时间初始化随机种子
srand(time(NULL));
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
// 生成点云数据1000个
cloud->width = 1000;
cloud->height = 1; // 1 表示点云为无序点云
cloud->points.resize(cloud->width * cloud->height);
// 给点云填充数据 0 - 1023
for (size_t i = 0; i < cloud->points.size(); ++i)
cloud->points[i].x = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[i].z = 1024.0f * rand() / (RAND_MAX + 1.0f);
// 创建KdTree的实现类KdTreeFLANN (Fast Library for Approximate Nearest Neighbor)
pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
// pcl::search::KdTree<pcl::PointXYZ> kdtree;
// 设置搜索空间,把cloud作为输入
kdtree.setInputCloud(cloud);
// 初始化一个随机的点,作为查询点
pcl::PointXYZ searchPoint;
searchPoint.x = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.y = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.z = 1024.0f * rand() / (RAND_MAX + 1.0f);
// K nearest neighbor search
// 方式一:搜索K个最近邻居
// 创建K和两个向量来保存搜索到的数据
// K = 10 表示搜索10个临近点
// pointIdxNKNSearch 保存搜索到的临近点的索引
// pointNKNSquaredDistance 保存对应临近点的距离的平方
int K = 10;
std::vector<int> pointIdxNKNSearch(K);
std::vector<float> pointNKNSquaredDistance(K);
std::cout << "K nearest neighbor search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with K=" << K << std::endl;
if (kdtree.nearestKSearch(searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0)
for (size_t i = 0; i < pointIdxNKNSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxNKNSearch[i]].x
<< " " << cloud->points[pointIdxNKNSearch[i]].y
<< " " << cloud->points[pointIdxNKNSearch[i]].z
<< " (距离平方: " << pointNKNSquaredDistance[i] << ")" << std::endl;
// Neighbors within radius search
// 方式二:通过指定半径搜索
std::vector<int> pointIdxRadiusSearch;
std::vector<float> pointRadiusSquaredDistance;
// 创建一个随机[0,256)的半径值
float radius = 256.0f * rand() / (RAND_MAX + 1.0f);
std::cout << "Neighbors within radius search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with radius=" << radius << std::endl;
if (kdtree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0)
for (size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
std::cout << " " << cloud->points[pointIdxRadiusSearch[i]].x
<< " " << cloud->points[pointIdxRadiusSearch[i]].y
<< " " << cloud->points[pointIdxRadiusSearch[i]].z
<< " (距离平方:: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5);
viewer.addPointCloud<pcl::PointXYZ>(cloud, "cloud");
pcl::PointXYZ originPoint(0.0, 0.0, 0.0);
// 添加从原点到搜索点的线段
viewer.addLine(originPoint, searchPoint);
// 添加一个以搜索点为圆心,搜索半径为半径的球体
viewer.addSphere(searchPoint, radius, "sphere", 0);
// 添加一个放到200倍后的坐标系
viewer.addCoordinateSystem(200);
while (!viewer.wasStopped())
viewer.spinOnce();
return 0;
结果图如下:

以上是关于K-D Tree原理和应用的主要内容,如果未能解决你的问题,请参考以下文章