每日一读High-order Proximity Preserving Information Network Hashing
Posted 海轰Pro
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了每日一读High-order Proximity Preserving Information Network Hashing相关的知识,希望对你有一定的参考价值。
目录
- 简介
- 论文简介
- ABSTRACT
- 1 INTRODUCTION
- 2 RELATED WORK
- 3 A GENERAL FRAMEWORK OF INFORMATION NETWORK HASHING
- 4 INH-MF: INFORMATION NETWORK HASHING BASED ON MATRIX FACTORIZATION
- 5 EXPERIMENTS
- 6 CONCLUSIONS
- 结语

简介
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
【每日一读】每天浅读一篇论文,了解专业前沿知识,培养阅读习惯(阅读记录 仅供参考)
论文简介
原文链接:https://dl.acm.org/doi/10.1145/3219819.3220034
会议:KDD '18: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (CCF A类)
年度:2018年7月19日(发表日期)
ABSTRACT
信息网络嵌入是高效图分析的有效途径。然而,它仍然面临链路预测和节点推荐等问题的计算挑战,特别是随着网络规模的扩大。
散列是一种很有前途的方法,可以将这些问题加速几个数量级。
然而,先前的研究没有集中在寻找信息网络的二进制代码以保持高阶接近度。
由于矩阵分解 (MF) 统一并优于几种众所周知的保留高阶接近度的嵌入方法,我们提出了一种基于 MF 的信息网络哈希 (INH-MF) 算法,以学习可以保留高阶接近度的二进制代码.
我们还建议汉明子空间学习,每次只更新部分二进制代码,以扩大 INHMF
我们最终在四个真实世界的信息网络数据集上评估 INH-MF 关于节点分类和节点推荐的任务。结果表明,INH-MF 在这两个任务中的性能明显优于竞争学习以散列基线,并且在节点推荐任务中优于网络嵌入方法,包括 DeepWalk、LINE 和 NetMF。 INH-MF 的源代码可在线获取 1
1 INTRODUCTION
信息网络在广泛多样的现实世界场景中无处不在,例如社交网络、道路网络、通信网络和万维网。有效的网络分析可以使许多应用程序受益,从蛋白质的角色分类 [13] 到向用户推荐新朋友 [2]。网络嵌入,学习网络的低维实值向量表示,成为后续高效网络分析的有效途径,如节点分类/聚类/推荐和链接预测。最近,许多努力致力于以显式或隐式方式提高在网络中保持高阶邻近性的能力,例如 DeepWalk [27]、LINE(二阶)[35]、node2vec [12]、 Grarep [7]、NetMF [28] 和 HOPE [26]。
但是,它在节点推荐和链接预测等问题上仍然面临计算挑战。例如,如果 d 是表示的维度,则在大小为 n 的社交网络中为所有用户推荐新朋友会花费 O(n2d)。由于现实世界的社交网络可能包含数亿个节点,因此这种计算成本在实践中将非常高。此外,随着社交网络由于添加/删除新边而不断发展,网络嵌入算法会频繁更新表示,并相应地更新推荐朋友列表。这些问题的关键是k-最近邻(knn)搜索,即为给定的“查询”节点寻找前k个最“相似”的节点。众所周知,散列是一种很有前途的快速相似性搜索方法[37]。这不仅归因于用快速汉明距离计算代替点积相似度计算,还归因于索引结构的使用,例如多索引哈希[25],它可能具有亚线性运行时行为。然而,据我们所知,之前没有研究专注于为信息网络寻求二进制表示(称为二进制代码)以保持高阶接近性。
阻碍直接利用图散列 [17、20、22、23、32] 或其他现有的散列学习方法的关键障碍,包括谱散列 (SH) [38]、归纳流形散列 (IMH) [31] 和交互式量化(ITQ)[11],学习二进制代码有两个方面。首先,即使在图哈希方法中也没有保留高阶接近度,但在网络嵌入中起着非常重要的作用。请注意,图哈希方法通常应用于从非关系数据构建的图上。其次,用于表示信息网络的邻接矩阵通常非常稀疏。 ITQ 和 SH 等方法无法处理稀疏矩阵,因为它们不可避免地依赖于 PCA,由于零中心,PCA 会将稀疏矩阵转换为密集矩阵。协同过滤的散列方法[39]也不同,因为它们处理二分图并且必须散列两种类型的节点。相比之下,我们专注于同构图,其中所有节点都属于同一类型,但每个节点都扮演两个角色:节点本身和其他节点的“上下文”[35]。因此,没有必要对节点的“上下文”角色进行散列。此外,在协同过滤的散列方法中几乎忽略了高阶邻近性保留。
为此,我们研究学习散列信息网络,这还没有得到很好的研究。在其中,信息网络被嵌入到低维二进制汉明空间中,同时解决了稀疏性挑战并保留了节点之间的高阶接近度。根据最近的研究[28],矩阵分解(MF)统一了几种重要的嵌入算法,保留了高阶接近度,包括 DeepWalk、LINE 和 node2vec,并显示出优于它们的性能。因此,我们提出了一种基于 MF 的信息网络哈希 (INH-MF) 算法,以同时减轻稀疏性并保持高阶接近度。众所周知,由于二进制约束[14],获得节点的最佳二进制代码通常是 NP-hard。因此,我们采用交替优化来直接解决具有挑战性的混合整数问题。我们发现对节点的“上下文”角色表示的正交约束将导致更新二进制代码的封闭形式。为了扩大 INH-MF,我们进一步建议汉明子空间学习,它每次只更新部分二进制代码。我们最终在节点分类和节点推荐任务方面评估了 INH-MF 在四个真实世界信息网络数据集上的有效性和效率。请注意,节点分类通常用于评估网络嵌入的有效性。结果表明,INH-MF 在节点推荐任务中的性能明显优于几种竞争学习哈希算法,并且出人意料地优于网络嵌入算法,包括 LINE、DeepWalk 和 NetMF。
总而言之,我们做出以下贡献:
- 我们首次研究学习散列信息网络,旨在显着加速依赖 knn 的网络分析,并展示其独特的特征和挑战。
- 我们提出了一种基于矩阵分解的信息网络哈希算法(INH-MF),可以解决稀疏性挑战并保持高阶接近度,并开发了一种基于交替优化的高效参数学习算法,可以以接近的形式更新参数。
- 我们建议使用汉明子空间学习来处理由于高阶邻近性保留而不断增长的网络密度。评估结果表明,它可以显着加快 INH-MF,而对节点分类性能的牺牲很小。
- 我们在四个真实世界的信息网络数据集上广泛评估 INH-MF。结果不仅表明 INH-MF 优于竞争性学习以散列基线,而且还表明二进制表示在节点推荐方面比实值表示更好。
2 RELATED WORK
这篇论文是关于无监督网络哈希的,所以我们主要回顾无监督的哈希算法,特别是图哈希,然后是网络嵌入的最新进展。
2.1 Learning to Hash
学习散列算法可以分为两类[37]:两阶段方法和离散散列。
两阶段方法首先导出实值特征学习,然后应用量化方法获得二进制代码。
- 例如,Salakhutdinov 和 Hinton [29] 提出了语义哈希 (SH) 来通过受限玻尔兹曼机学习二进制代码,以快速搜索相似的文档。
- 韦斯等人。将光谱分析技术应用于数据点之间构建的相似图,并将其嵌入到低维空间中[38]。
- 此外,这项工作引入了平衡和不相关的约束来推导紧凑的二进制代码。刘等人。提出了锚图散列以扩大谱分析[23]。沉等人。提出了用于利用流形结构的归纳流形散列(IMH)[31]。
- 注意到每个 PCA 方向上的数据方差是不同的,Gong 等人。
- 提出了迭代量化来旋转表示以获得更有效的二进制代码[11]。
- [19] 中也研究了类似的想法,目标是各向同性方差。请注意,除了 IMH 和 SH 之外的方法不可避免地依赖于 PCA,由于零中心,PCA 不适用于大型稀疏矩阵。离散散列直接学习二进制代码。例如,离散图哈希[22]、监督离散哈希[30]、非对称离散图哈希[32]和可伸缩图哈希[17]被提出用于联合优化量化损失和内在目标函数。
最近,离散散列的思想也被应用于基于散列的推荐系统(RS)[21、39、40]。然而,RS 中的评级数据可以组织为二分图,不同于同构网络,如前所述。
2.2 Network Embedding
正如 [8, 35] 中所讨论的,网络嵌入也不同于 IsoMap 和 MDS 等图嵌入。
因此,开创性的工作是 DeepWalk [27] 和 Graph Factorization [1]。
- Graph Factorization 直接分解邻接矩阵得到一个低维向量。
- DeepWalk 首先在网络上采用截断的随机游走来生成一组游走序列,并应用 Skip-Gram 来获得节点的嵌入。
- 与 DeepWalk 类似,node2vec [12] 也优化了嵌入以编码随机游走的统计信息,但设计了一种二阶随机游走策略来采样相邻节点。
- LINE [35] 被提出用于大规模网络嵌入,并且可以保持一阶和二阶接近度
- 。 Grarep [7] 证明在构建节点的全局表示时也应该捕获 k 阶接近度。
最近,为了统一 DeepWalk、node2vec 和 LINE,提出了一个通用的矩阵分解框架,其中 LINE 是 DeepWalk 的一个特例。 HOPE [26] 在一个通用公式中总结了高阶接近度的四个测量值,然后应用广义 SVD 来获得节点嵌入。
邻域聚合是另一个嵌入框架,包括图卷积网络 [18] 和 structure2vec [9]。有关网络嵌入的更多文献,请参阅最近的调查论文,例如 [4, 8]。
3 A GENERAL FRAMEWORK OF INFORMATION NETWORK HASHING
3.1 Problem Statement
信息网络定义为 G = <V , E>,其中 V 是大小为 n = |V | 的顶点/节点的集合。 E 是节点之间的边集,代表一种关系。 G可以用一个邻接矩阵A来表示,其中Ai,j是节点i和节点j之间的边权重,表示关系的强度。节点之间的高阶邻近矩阵由另一个矩阵S表示,应该通过网络嵌入来保留。二阶邻近矩阵与邻接矩阵直接相关,k阶邻近矩阵可以由(k-1)阶邻近矩阵构成。在[7, 28]中可以参考几种构建方式。有了这些符号,我们就定义了信息网络散列问题。
定义 3.1(信息网络散列)。给定一个信息网络 G = <V , E>,信息网络哈希问题旨在将每个节点 v ∈ V 表示为一个低维汉明空间 ±1d ,即学习一个哈希函数 hG : V → ±1d ,其中 d n。在这个空间±1d 中,不仅要保留节点之间的高阶接近度,还要尽可能满足比特不相关和平衡条件。
[38] 引入了比特不相关和平衡条件来近似码平衡条件:映射到每个二进制码的数据项的数量是相同的。位平衡是指每个位为 1 或 -1 的机会几乎相等,相当于最大化每个位的熵。位不相关意味着不同的位是不相关的,通常通过正交约束来实现。
3.2 Overview
信息网络散列是基于通过离散散列学习散列算法,即将二进制代码作为参数并直接学习这些代码。节点 i 的二进制代码表示为列向量 bi ∈ ±1d ,它只捕获节点本身的角色。节点 i 的“上下文”角色由列向量 qi ∈ Rd 表示,可能带有一些约束。我们还表示 B = [b1,···, bn ]T,大小为 n × d 的矩阵,Q = [q1,···,qn ]T,大小为 n × d 的矩阵。然后位不相关和平衡分别由BT B = nId 和BT 1n = 0 实现,其中1 是长度为n 且全为1 的向量。请注意,这两个条件可能并不严格满足。例如,如果n为奇数,则BT 1n 0。因此,我们只保证尽可能地满足它们。类似地,很可能对 Q 施加约束,例如谱范数 ‖Q ‖2 ≤ 1 或 QT Q = Id 。我们将 Q 表示为具有这些约束的一组 Q。基于 B 和 Q,节点 i 和 j 之间的接近度估计为
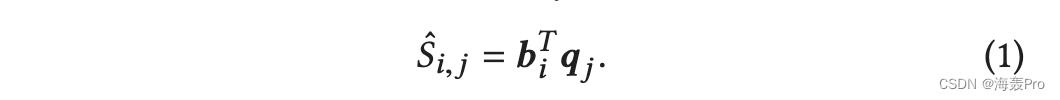
因此信息网络散列的损失函数可以定义为
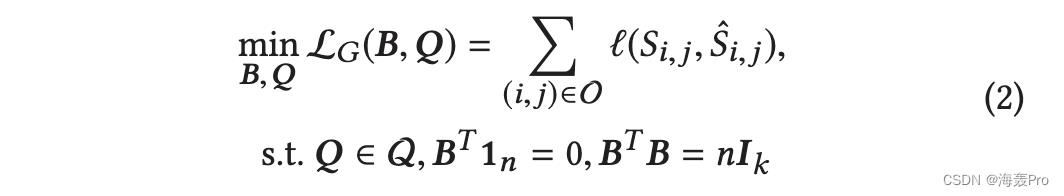
其中 O 表示边缘集,必须考虑其边缘以保持邻近度,并且 (x, y) 是损失函数,可以平方损失 (x, y) = (x − y)2 ,绝对损失 ( x, y) =|x - y|。它也可以用基于排名的损失函数代替,用于基于排名的信息网络哈希。
4 INH-MF: INFORMATION NETWORK HASHING BASED ON MATRIX FACTORIZATION
在本节中,基于信息网络散列的一般框架,我们提出其实例之一——基于矩阵分解的信息网络散列(INH-MF)。
4.1 Preliminary
矩阵分解在本文中用于散列信息网络,因为它已被证明可以统一 DeepWalk、node2vec 和 LINE,并且根据 [28] 显示出优于它们的性能。特别是,DeepWalk 隐式逼近和分解以下矩阵

其中 vol(G) = i j Ai, j 是信息网络的体积 G,D = diag([d1, · · · , dn ]) 式中 di 表示节点 i 的广义程度,T 表示上下文窗口大小 (T + 1是接近的顺序),b是skip-gram中的负样本数。 LINE(2nd) 是 DeepWalk 的一个特例,通过设置 T = 1,即
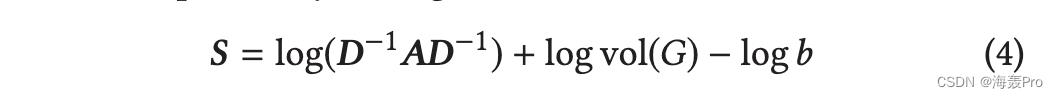
因此,与 Graph Factorization 不同,LINE 通过两个连接节点的泛化程度对每条边的权重进行归一化。根据 LINE [35] 的实验结果,这样的归一化步骤在网络嵌入中起着重要作用。还有其他构造高阶邻近矩阵的方法[7, 26],但不再讨论。
为了获得保留 k 阶接近度的网络嵌入,建议通过设置 T = k - 1 来分解等式 (3) 中的接近度矩阵 S 的截断奇异值分解 (SVD)。特别是,S ≈ U d ΣdV T d , 然后根据 [7, 28] 建议将节点嵌入为 U d Σ 1 2d 的对应行。
4.2 Model Description
为节点导出二进制代码的一种直接方法是将符号函数应用于获得的网络嵌入,即 B = sign(U d Σ 1 2d )。这种导出二进制代码的方法称为两阶段方法。然而,根据 [22, 30, 39],两阶段方法可能会产生较大的量化损失。他们表明,将散列码视为学习参数的离散散列是一种更有前途的替代方案。接下来,我们首先推导出离散散列的损失函数。
截断奇异值分解 Sd = U d ΣdV T d 是 S [ 3] 的最佳 rank-d 近似值,即 ‖S - Sd ‖F ≤ ‖S - B‖F ,其中 B 是最多秩的任意矩阵d。因此,我们可以将截断的 SVD 表示为以下优化问题

由于每个有限维矩阵都有一个秩分解 B =PQT ,其中 P, Q ∈ Rn×d ,这个优化可以重写为
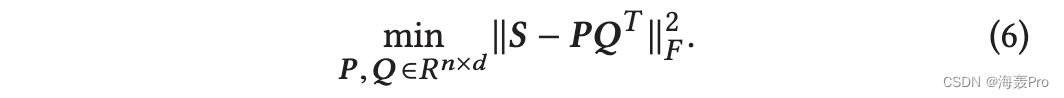
这里我们假设 P 和 Q 分别对应节点本身的角色和其他节点的“上下文”。这个损失函数不是关于 (P, Q) 的凸函数,而是在给定另一个固定的情况下关于 P 或 Q 的凸函数。这个目标函数的所有局部最小值都是全局的[33]。因此,建议交替优化,并且可以对 Q 施加列正交约束,即 QT Q = Ik ,以加快下降速度。固定Q时,P=SQ最优;在固定 P 时,minQ ‖S − PQT ‖等价于 maxQ trace(QT ST P),它也具有更新规则的封闭形式。后一种优化将在下一小节中详细说明。请注意,当 Q = V d 且 P = SQ 时,关于 (P, Q) 的梯度消失。因此,(SV d , V d ) 是该目标函数的临界点。
由于 P 对应于节点的嵌入,因此最好通过对旋转的 ^P = PW 应用阈值函数来获得二进制代码 B,其中 W ∈ Rk ×k 是正交矩阵 [11]。那么PQT = ^P(QW )T 。为了离散散列,将 ^P 替换为 B,直接从 S 中学习。由于 (QW )T QW = Id ,记作 ^Q = QW ,学习散列信息网络的目标函数公式如下:
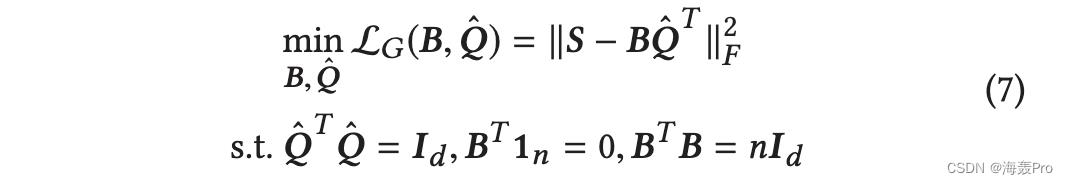
其中施加了比特平衡和不相关约束。而 ^Q 起到两个作用:降维和基旋转。随后,为方便起见,Q上方的帽子将被丢弃。
4.3 Model Optimization
由于二进制约束,获得最优二进制代码是 NPhard。因此,我们采用交替优化,在其他固定参数的情况下轮流更新每个参数。接下来,我们推导出 B 和 Q 的更新规则。
4.4 Hamming Subspace Learning
由于在网络嵌入中通常会保留高阶接近度,因此接近度矩阵 S 可能会变得比 A 密集得多,因此在保留了高阶接近度的情况下获得网络嵌入会花费更多的时间。为了扩展信息网络哈希算法,我们建议汉明子空间学习,每次更新部分二进制代码,类似于[24]。接下来,我们将介绍如何设计一个损失函数来选择一个比特子集进行更新。假设 e ∈ 0, 1d 是位选择变量,如果选择了二进制码的第 i 位,则 ei = 1。然后我们优化以下函数 w.r.t e
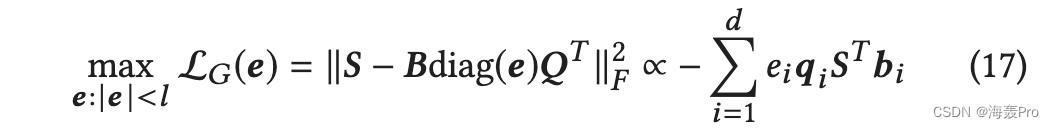
其中 l 是选择的位数。这个优化问题旨在找到最差拟合的子空间来更新二进制代码的相应位,类似于 [34]。显然,这种优化有一个最优解。也就是我们先用qi ST bi 对第i 位进行打分,然后选择打分最小的l 位。
4.5 Initialization
如前所述,获得最佳二进制代码是 NP 难的,因此良好的二进制代码初始化很重要。稀疏矩阵上截断的 SVD 可能效率不高,甚至无法返回收敛的奇异向量,实验中 scipy 的 svds 例程在 50% 的 Flickr 数据集上的运行时错误证明了这一点。因此,我们通过交替优化来解决方程(6)中的问题以获得(P,Q)。然后通过设置Φ = P,通过方程(15)初始化 B。也可以通过用实值矩阵替换 B 来解决方程(7)的松弛问题,但它将留待以后的工作。
4.6 Convergence and Complexity
5 EXPERIMENTS
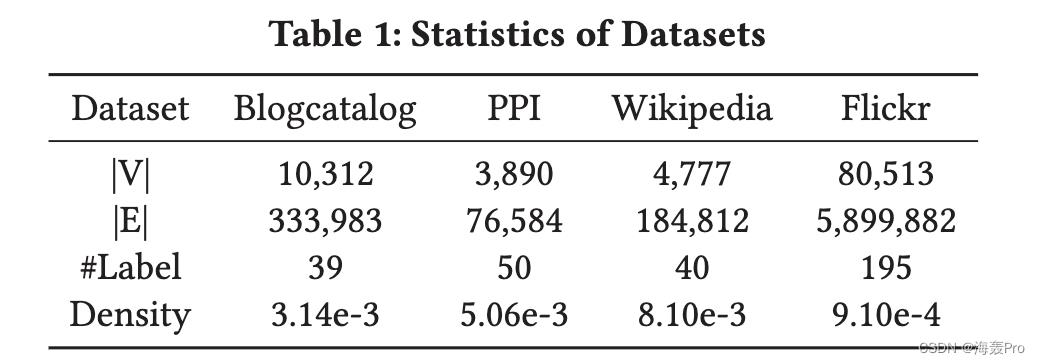
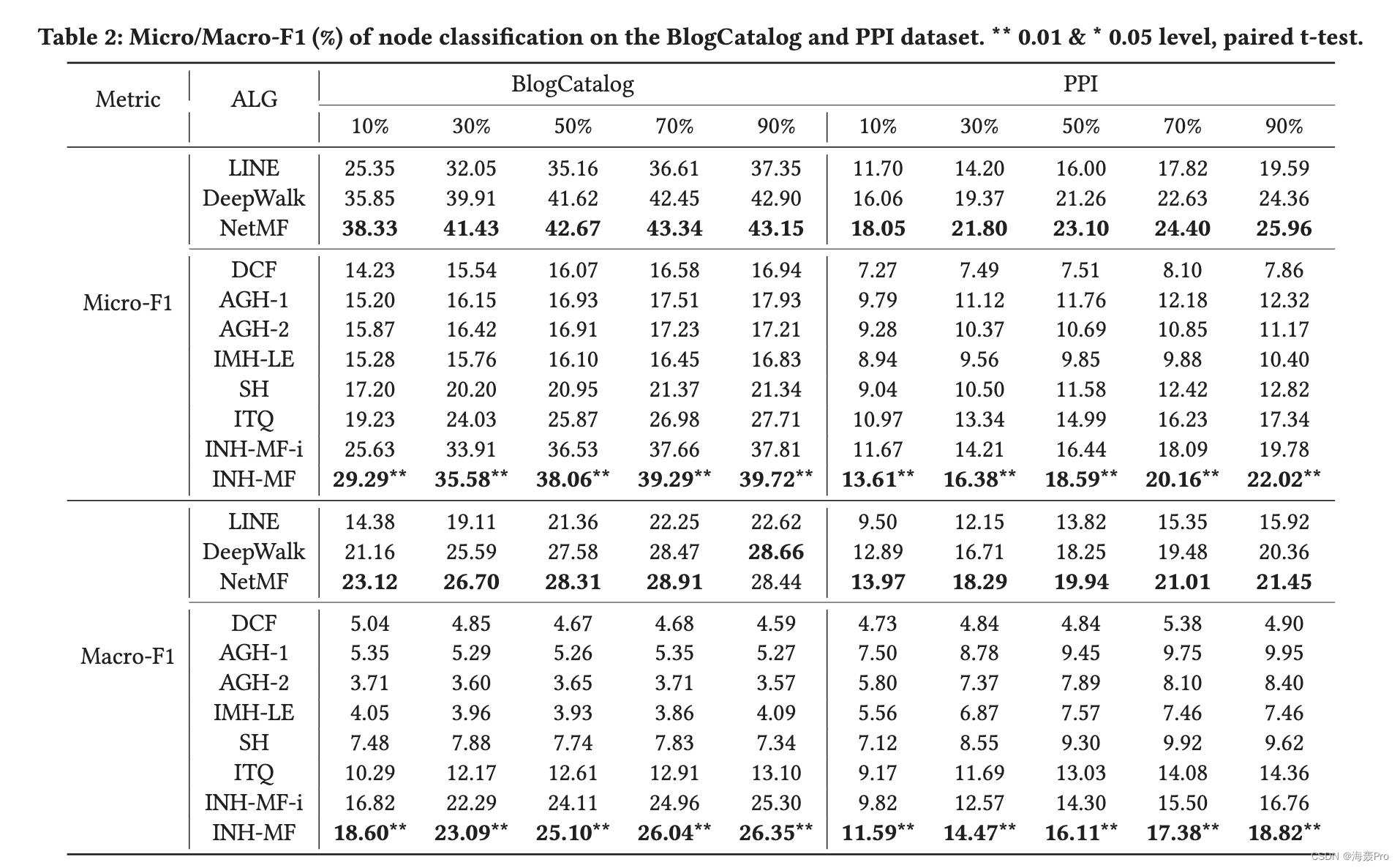
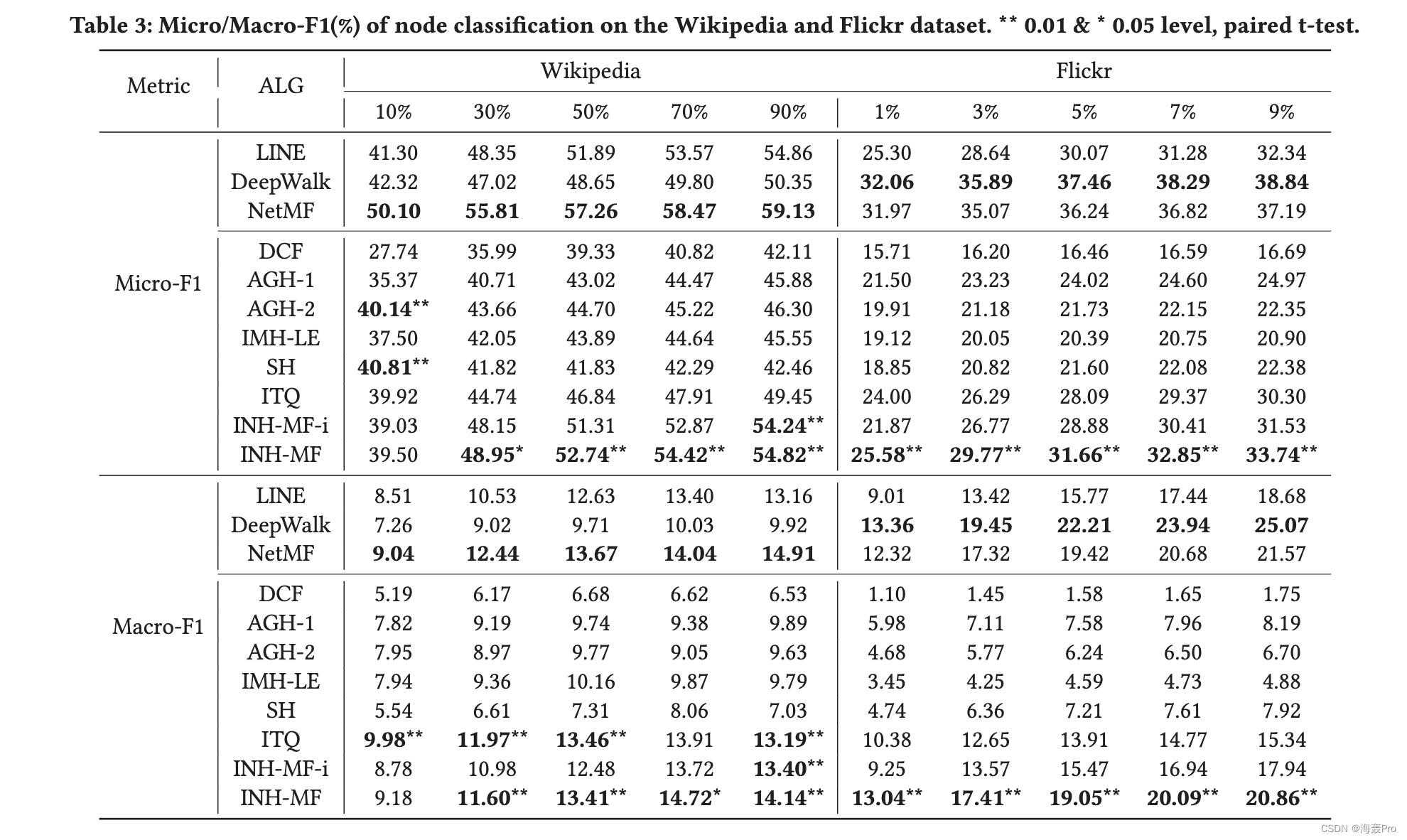
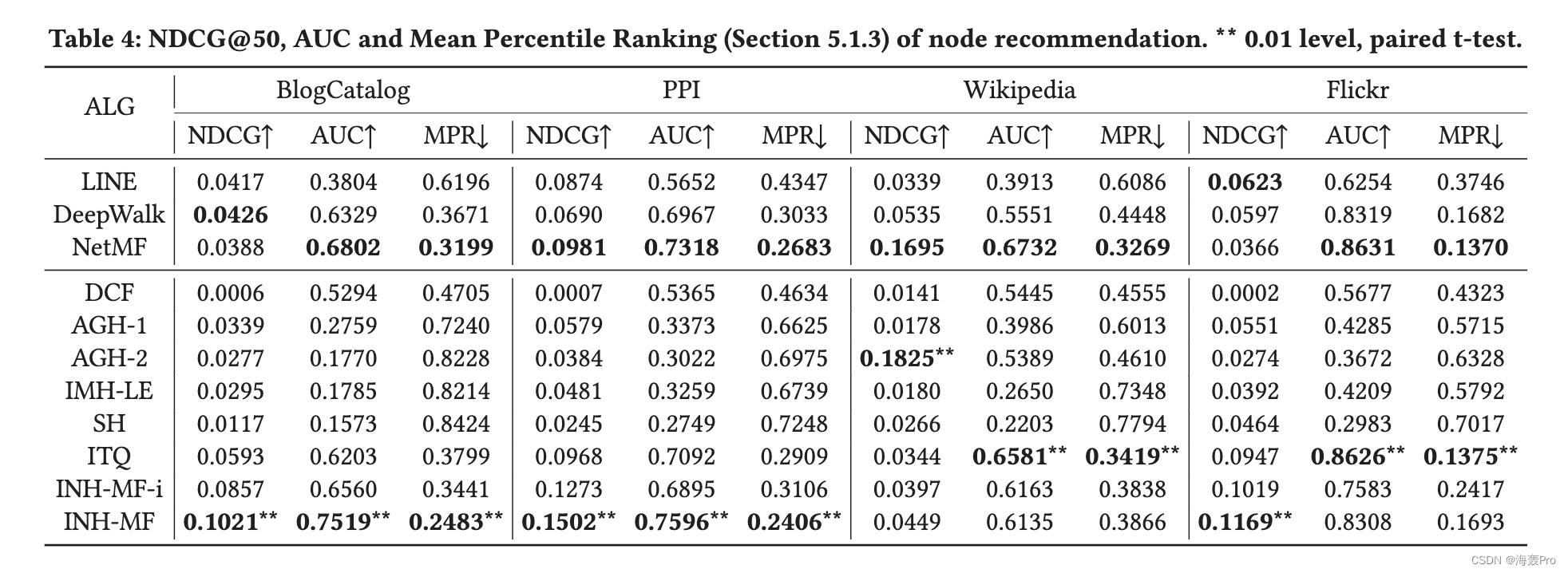
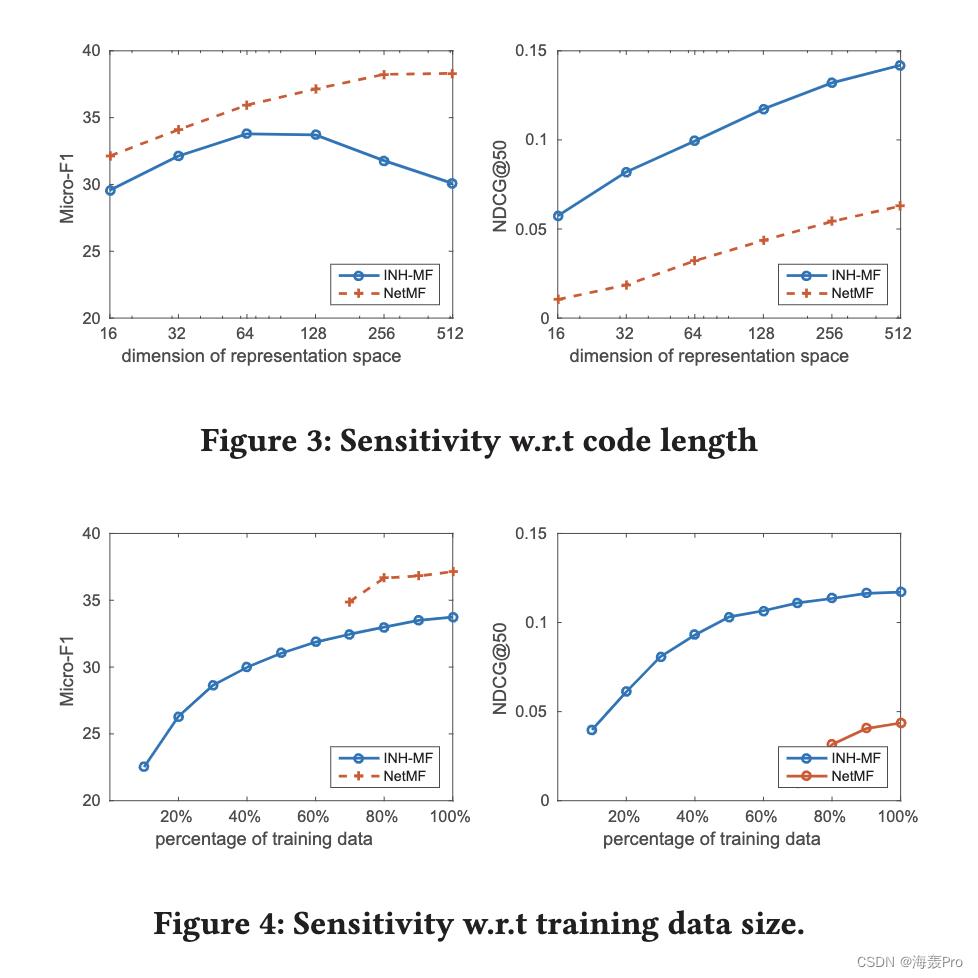
在本节中,我们针对节点分类和节点推荐 [8] 的常用任务评估 INH-MF。这两项任务对于评估网络嵌入的有效性至关重要。后一项任务对于评估由于散列导致的效率改进也很有用。

6 CONCLUSIONS
本文研究了信息网络哈希学习问题,提出了一种基于MF的信息网络哈希算法,该算法可以保持高阶接近度。
我们为学习参数开发了一种有效的交替优化算法,并建议使用汉明子空间学习进行扩展。我们在节点分类和节点推荐方面在四个真实世界的网络数据集上广泛评估了所提出的算法(INH-MF)。
在这两项任务中,INH-MF 在三个数据集上的表现都明显优于竞争学习哈希算法。
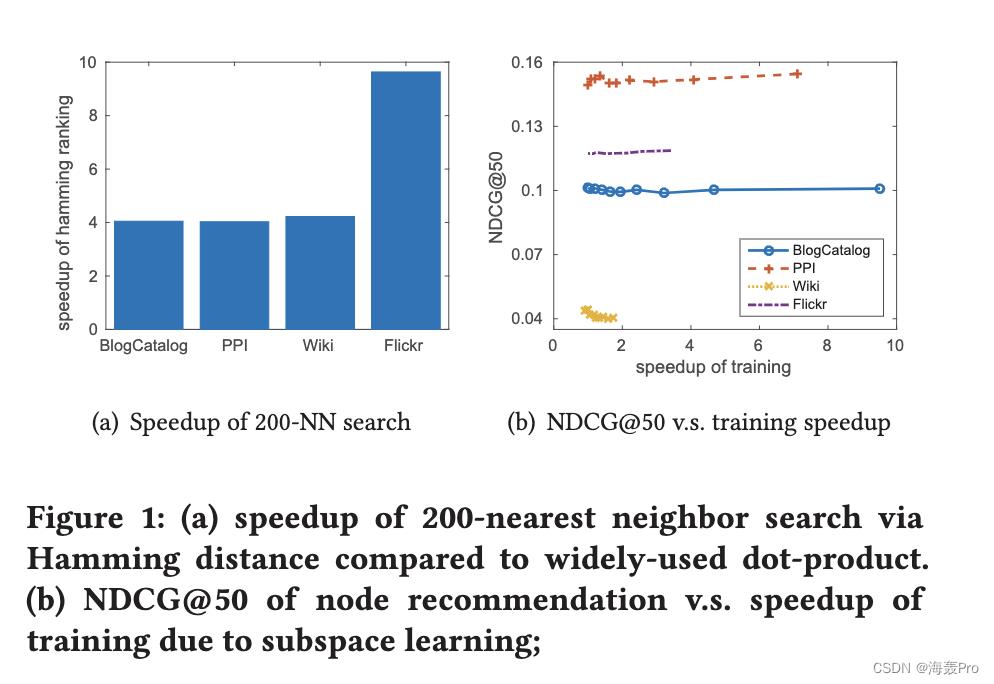
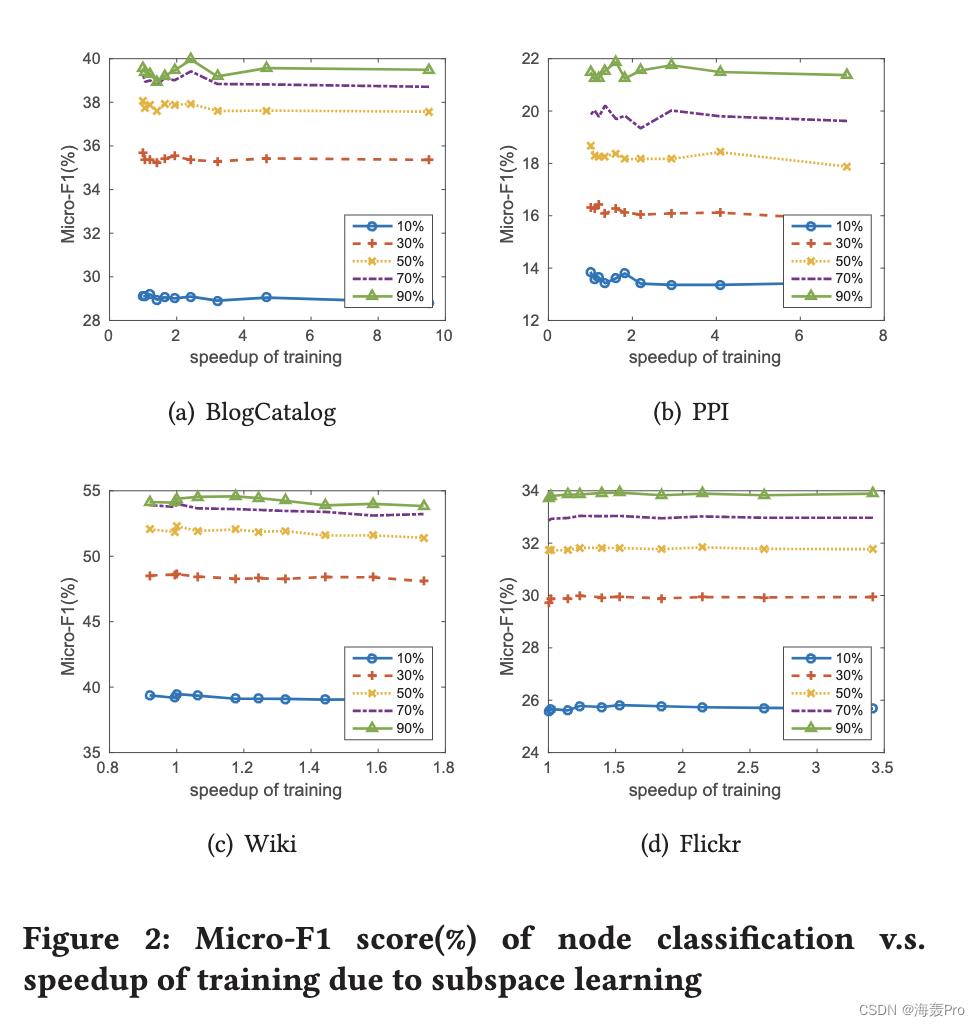
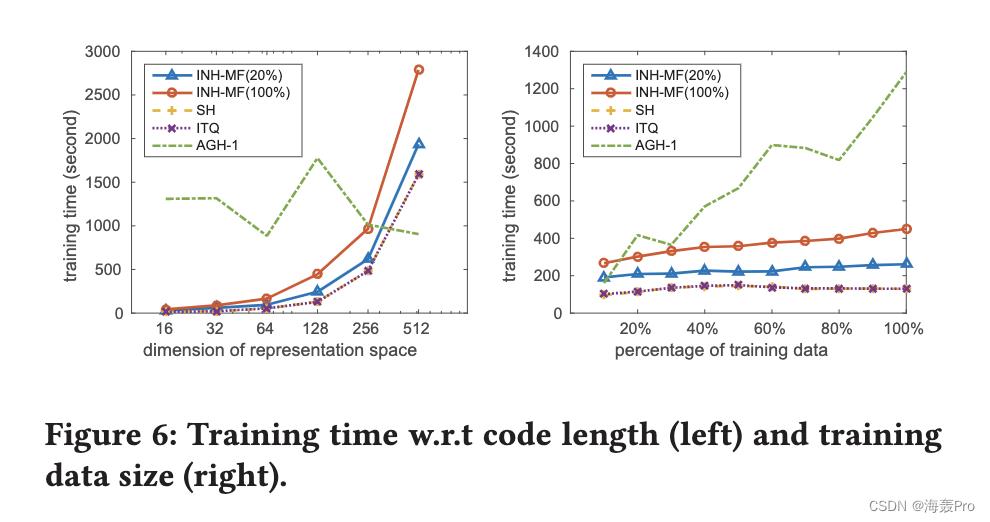
在大多数情况下,在节点推荐方面,INH-MF 可以出人意料地优于所有网络嵌入算法。而在节点分类任务中,INH-MF 几乎优于 LINE,但总体上略逊于 NetMF 和 DeepWalk,有时甚至可以与之媲美。此外,由于子空间学习,INH-MF 显示出节点推荐和参数学习的显着加速。
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

以上是关于每日一读High-order Proximity Preserving Information Network Hashing的主要内容,如果未能解决你的问题,请参考以下文章