每日一读Joint Unsupervised Learning of Deep Representations and Image Clusters

Posted 2022-12-15 海轰Pro

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了每日一读Joint Unsupervised Learning of Deep Representations and Image Clusters相关的知识，希望对你有一定的参考价值。

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

唯有努力💪

【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/7780925

会议： 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) （CCF A类）

年度：2016年6月27日至30日（发表日期）

源代码：https://github.com/jwyang/joint-unsupervised-learning

Abstract

在本文中，我们提出了一种用于深度表示和图像集群的联合无监督学习的循环框架。

在我们的框架中，聚类算法中的连续操作表示为循环过程中的步骤，堆叠在卷积神经网络 (CNN) 输出的表示之上。在训练过程中，图像聚类和表征被联合更新：图像聚类在前向传播中进行，而表征学习在后向传播中进行。

我们在这个框架背后的关键思想是良好的表示有利于图像聚类，聚类结果为表示学习提供监督信号。通过将两个过程集成到具有统一加权三元组损失函数的单个模型中并对其进行端到端优化，我们不仅可以获得更强大的表示，还可以获得更精确的图像聚类。

大量实验表明，我们的方法在跨各种图像数据集的图像聚类方面优于最先进的方法。此外，学习到的表示在转移到其他任务时可以很好地泛化。

1. Introduction

我们正在目睹视觉内容的爆炸式增长。机器学习和计算机视觉的最新进展，特别是通过深度神经网络，依赖于监督学习和大量注释数据的可用性。然而，手动标记数据是一个耗时、费力且通常昂贵的过程。为了更好地利用可用的未标记图像，聚类和/或无监督学习是一个很有前途的方向。

在这项工作中，我们的目标是在一个统一的框架中解决未标记图像的图像聚类和表示学习。利用图像的集群 ID 作为监督信号来学习表示是一个自然的想法，而这些表示反过来将有利于图像聚类。 在高级视图中，给定 $n_s$ 未标记图像的集合 $I = \\I_1, ..., I_n_s \\$ ，用于学习图像表示和聚类的全局目标函数可以写为：

其中 L(·) 是损失函数，y 表示所有图像的簇 id，θ 表示表示的参数。如果我们将 y, θ 中的一个固定，优化可以分解为两个交替的步骤：

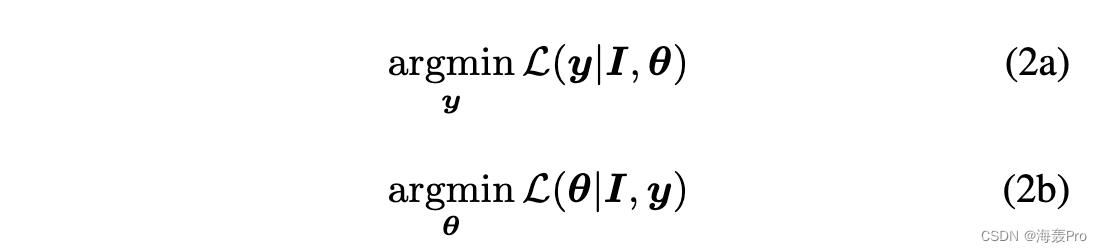
直观地说，（2a）可以看作是基于固定表示的传统聚类问题，而（2b）是标准的监督表示学习过程。

在本文中，我们提出了一种在两个步骤之间交替的方法——在给定当前表示参数的情况下更新集群 ID，并在给定当前聚类结果的情况下更新表示参数。具体来说，我们使用凝聚聚类[16] 对图像进行聚类，并通过卷积神经网络 (CNN) 的激活来表示图像。

选择凝聚聚类的原因有三个：

1）它以过度聚类开始，当尚未学习到好的表示时，它在开始时更可靠。直观地说，用随机权重初始化的 CNN 表示的聚类是不可靠的，但最近邻和过度聚类通常是可以接受的；
2）随着学习到更好的表示，这些过度聚类可以被合并；
3）凝聚聚类是一个循环过程，可以自然地在循环框架中进行解释。

我们的最终算法非常直观。我们从初始过度聚类开始，使用图像聚类标签作为监督信号更新 CNN 参数 (2b)，然后合并聚类 (2a) 并迭代直到达到停止标准。

所提出框架的结果如图 1 所示。

最初，MNIST 测试集（10k 个样本）有 1,762 个集群，并且表示（图像强度）不是那么具有区分性。
经过几次迭代，我们获得了 17 个聚类和更具判别性的表示。
最后，我们获得了 10 个集群，它们被学习的表示很好地分离，并且有趣地主要对应于数据集中的 groundtruth 类别标签，即使表示是以无监督的方式学习的。

总而言之，我们工作的主要贡献是：

我们提出了一个简单但有效的端到端学习框架，以从未标记的图像集中共同学习深度表示和图像集群；
我们在循环框架中制定联合学习，其中凝聚聚类的合并操作表示为前向传递，而 CNN 的表示学习表示为后向传递；
我们推导出一个单一的损失函数来指导凝聚聚类和深度表示学习，这使得两个任务的优化无缝；
我们的实验结果表明，所提出的框架优于以前的图像聚类方法，并且学习了可以转移到其他任务和数据集的深度表示。

2. Related Work

聚类

聚类算法可以大致分为层次和分区方法[24]

凝聚聚类是一种层次聚类算法，从许多小聚类开始，然后逐渐合并聚类[12,16,30]
至于分区聚类方法，最著名的是 K-means [36]，它可以最小化数据点与其最近的聚类中心之间的平方误差之和。相关思想构成了许多方法的基础，例如期望最大化 (EM) [7, 37]、谱聚类 [40, 47, 61] 和基于非负矩阵分解 (NMF) 的聚类 [1, 8, 60]。

深度表示学习许多作品使用原始图像强度或手工制作的特征 [9, 18, 19, 23, 42, 50] 与传统的聚类方法相结合。

最近，使用深度神经网络学习的表示在许多计算机视觉任务上比手工设计的特征有了显着改进，例如图像分类 [29、44、46、49]、对象检测 [13、14、20、43] 等然而，这些方法依赖于使用大量标记数据的监督学习来学习丰富的表示。许多工作都集中在从未标记的图像数据中学习表示。

一类方法迎合重建任务，例如自动编码器 [21、28、33、41、53]、深度信念网络 (DBN) [31] 等。

另一组技术在为图像制作监督信号后学习判别表示，然后针对下游应用对它们进行有监督的微调 [10, 11, 55]。

与我们的方法不同，在这些先前的工作中制造的监督信号在表示学习期间不会更新。

组合

许多作品探索了将图像聚类与表示学习相结合

在 [51] 中，作者提出使用堆叠自动编码器学习无向亲和图的非线性嵌入，然后在嵌入空间中运行 K-means 以获得聚类。
在 [52] 中，使用深度半 NMF 模型将输入分解为多个堆叠因子，这些堆叠因子逐层初始化和更新。使用顶层的表示，实施 K-means 以获得最终结果。与我们的工作不同，它们没有针对表示学习和聚类进行联合优化。

为了更紧密地连接图像聚类和表示学习

[58]迭代地进行了图像聚类和码本学习。然而，他们通过 SIFT 特征 [35] 学习了码本，并没有学习深度表示。
Chen [2] 没有使用手工制作的特征，而是使用 DBN 来学习表示，然后对 DBN 的输出进行非参数最大边距聚类。之后，他们根据聚类结果对 DBN 的顶层进行了微调。
在 [56] 中发现了一项关于联合优化两个任务的最新工作，其中作者训练了一个特定于任务的深度聚类架构。深度架构由稀疏编码模块组成，这些模块可以通过面向集群的损失的反向传播进行联合训练。然而，他们使用稀疏编码来提取图像的表示，而我们使用 CNN。我们没有将聚类的数量固定为类别的数量和基于 softmax 输出的预测标签，而是使用基于学习表示的凝聚聚类来预测标签。在我们的实验中，我们表明我们的方法优于 [56]。

3. Approach

3.1. Notation

我们用 $I =\\I_1, ..., I_n_s \\$ 表示具有 $n_s$ 个图像的图像集。该图像集的集群标签 $y = \\y_1, ..., y_n_s \\$ 。 θ 是 CNN 参数，基于它我们从 $I$ 中获得深度表示 $X = \\x_1, ..., x_n_s \\$ 。

给定预测的图像簇标签，我们将它们组织成 $n_c$ 簇 $C = \\C_1, ... , C_n_c \\$ , 其中 $C_i = \\x_k|y_k = i, ∀k ∈ 1, ..., n_s\\$ 。 $N^Ks_i$ 是 $x_i$ 的 $K_s$ 最近邻居， $N^Kc_C_i$ 是 $C_i$ 的 $K_c$ 最近邻簇的集合。

为方便起见，我们将 $N^K_c_C_i$ 中的集群按照与 $C_i$ 的亲和性降序排列，使得最近邻 $\\quad max_C∈C_t A(C_i, C)$ 是第一个条目 $N^K_c_C_i$ [1]。这里，A 是衡量两个集群之间的亲和度（或相似度）的函数。我们在 θ, X, y, C 添加上标 t 来表示它们在时间步 t 的状态。我们使用 Y 来表示具有 T 个时间步长的序列 $y^1, ..., y^T \\$ 。

3.2. Agglomerative Clustering

作为背景，我们首先简要描述传统的凝聚聚类[16, 30]。凝聚聚类的核心思想是在每一步合并两个聚类，直到某些停止条件。在数学上，它试图通过以下方式找到两个簇 Ca 和 Cb

有很多方法可以计算两个集群之间的亲和力 [16, 30, 38, 62, 64]。更多细节可以在[24]中找到。我们现在描述我们的方法是如何测量亲和力的。

3.3. Affinity Measure

首先，我们构建一个有向图 G =< V, E >，其中 Vis 是对应于 I 的深度表示 X 的顶点集合，E 是连接顶点的边集合。我们定义了一个对应于边集的亲和矩阵 W ∈ Rns ×ns。从顶点 xi 到 xj 的权重定义为

其中 σ2 = ans Ks∑xi ∈X∑xj ∈N Ks i||xi − xj ||2 2. 这种构建有向图的方法可以在许多先前的工作中找到，例如 [62, 64]。这里，a 和 Ks 是两个预定义的参数（它们的值在表 2 中列出）。

在为样本构建有向图之后，我们采用 [62] 中的图度链接来测量集群 Ci 和 Cj 之间的亲和度，记为 A(Ci, Cj)。

3.4. A Recurrent Framework

我们的主要见解是凝聚聚类可以解释为一个循环过程，因为它在多个时间步上合并聚类。基于这一见解，我们提出了一个循环框架来结合图像聚类和表示学习过程。

如图 2 所示，在时间步 t，图像 I 首先被输入 CNN 以获得表示 Xt，然后与之前的隐藏状态 ht-1 结合使用来预测当前隐藏状态 ht，即图像簇标签在时间步长。在我们的上下文中，时间步长 t 的输出是 yt = ht。因此，在时间步 t

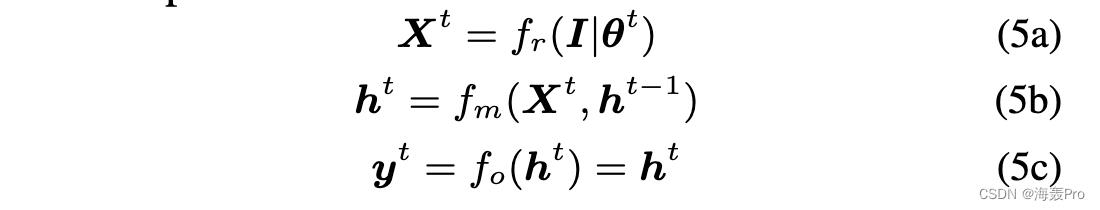
其中 fr 是使用 θt 参数化的 CNN 为输入 I 提取深度表示 Xt 的函数，fm 是基于 Xt 和 ht-1 生成 ht 的合并过程。

在典型的循环神经网络中，将在每次训练迭代中展开所有时间步长。在我们的例子中，这将涉及执行凝聚聚类，直到我们获得所需数量的聚类，然后通过反向传播更新 CNN 参数。

在这项工作中，我们引入了一种部分展开策略，即将整个 T 时间步分成多个时段，并且一次展开一个时段。我们部分展开的直观原因是 CNN 一开始的表示不可靠。我们需要更新 CNN 参数，以便为以下合并过程获得更多的判别表示。在每个周期中，我们合并多个集群并在周期结束时更新 CNN 参数以进行固定次数的迭代。一个极端的情况是每个周期一个时间步长，但它涉及过于频繁地更新 CNN 参数，因此非常耗时。因此，每个周期的时间步数（以及每个周期合并的集群数量）由我们方法中的参数确定。我们将在第 2 节中详细说明这一点。 3.6.

3.5. Objective Function

在我们的循环框架中，我们累积所有时间步的损失，公式为

在这里，y0 将每个图像作为一个集群。在时间步 t，我们找到两个集群来合并给定 yt-1。在传统的凝聚聚类中，两个聚类是通过找到所有聚类对的最大亲和力来确定的。在本文中，我们引入了一个标准，该标准不仅考虑了两个集群之间的亲和力，还考虑了集群周围的局部结构。假设从 yt−1 到 yt，我们合并了一个集群 Ct i 及其最近的邻居。那么时间步 t 的损失是负亲和度的组合，即

其中 λ 为 (7a) 和 (7b) 的权重。请注意，yt、yt-1 和 θta 没有明确显示在右侧，但它们通过图像集群标签和集群之间的亲和力来确定损失。在上述等式的右侧，有两项： 1) (7a) 衡量聚类 Ci 与其最近邻之间的亲和力，遵循传统的凝聚聚类； 2) (7b) 测量 Ci 与其最近邻簇的亲和力与 Ci 与其其他邻居簇的亲和力之间的差异。该术语考虑了局部结构。见秒。 3.5.1 详细解释。

很难同时推导出最优的y1, …, yT 和 θ1, …, θT 以最小化等式中的整体损失。 (6)。如前所述，我们在循环过程中迭代优化。我们将 T 个时间步分为 P 个部分展开的周期。在每个周期中，我们固定 θ 并在前向传播中搜索最优 y，然后在后向传播中，我们在给定最优 y 的情况下推导出最优 θ。详细信息将在以下部分中进行说明。

3.5.1 Forward Pass

在第 p 个 (p ∈ 1, …, P ) 部分展开周期的前向传递中，我们更新集群标签，将 θ 固定为 θp，周期 p 的整体损失为

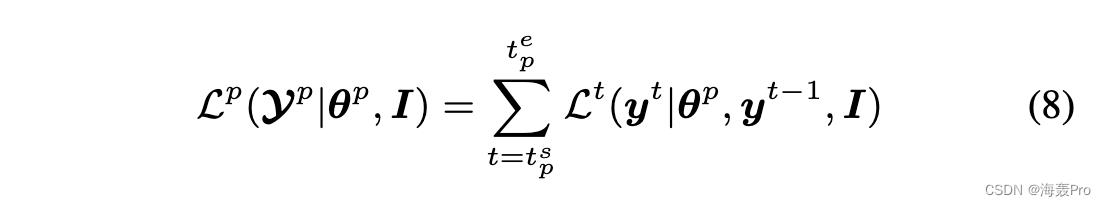
其中 Yp 是周期 p 中的图像标签序列，[ts p, te p] 是周期 p 中对应的时间步长。为了优化，我们遵循类似于传统凝聚聚类的贪婪搜索。从时间步 ts p 开始，它找到一个集群及其最近的邻居进行合并，以便在所有可能的集群对上最小化 Lt。

在图 3 中，我们提供了一个玩具示例来解释我们使用术语 (7b) 的原因。如图所示，通常情况下，集群在某些区域密集，而在其他一些区域稀疏。在传统的凝聚聚类中，无论聚类位于何处，它每次都会选择具有最大亲和力（或最小损失）的两个聚类。在这种特定情况下，它将选择集群 Cb 及其最近的邻居进行合并。相比之下，如图 3(b) 所示，我们的算法通过添加 (7b) 将找到集群 Ce，因为它不仅靠近它最近的邻居，而且距离它的其他邻居也相对较远，即本地结构被认为是围绕一个集群。引入 (7b) 的另一个优点是它允许我们用三元组来写损失，如下所述。

3.5.2 Backward Pass

在第 p 个部分展开期间的前向传递中，我们合并了许多集群。让最优图像簇标签序列由 Yp∗ = yt∗ 给出，在前向传播中合并的簇表示为 [Ct∗, N KcCt∗[1]],t ∈ ts p, … ., te p。在后向传播中，我们的目标是推导出最优 θ 以最小化前向传播中产生的损失。因为当前时期的聚类是以之前所有时期的聚类结果为条件的，所以我们将所有 p 个时期的损失累加起来，即

最小化 (9) w.r.t θ 导致在 Y1∗, …, Yp∗ 或 y1∗, …, yte p∗ 监督下的 I 上的表示学习。基于（7a）和（7b），方程中的损失。 9 被重新表述为

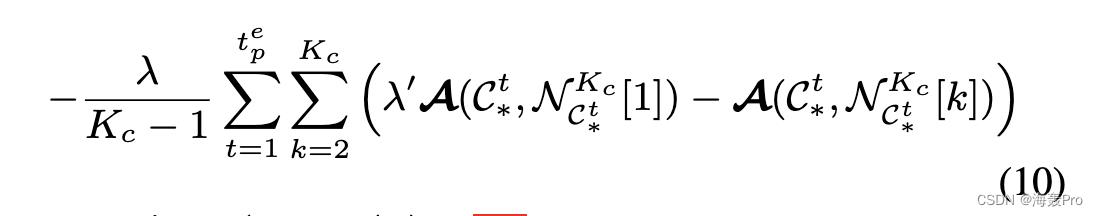
其中λ′ = (1 + 1/λ)。 (10) 是在点簇上定义的损失，需要整个数据集进行估计，因此难以使用基于批处理的优化。然而，我们表明这种损失可以通过基于样本的损失来近似，使我们能够使用批量统计计算梯度的无偏估计量。

重新制定损失背后的直觉是凝聚聚类从每个数据点作为一个聚类开始，层次结构中较高级别的聚类是通过合并较低级别的聚类形成的。因此，集群之间的亲和力可以用数据点之间的亲和力来表示。我们在补充中表明，（10）中的损失可以近似地重新表述为

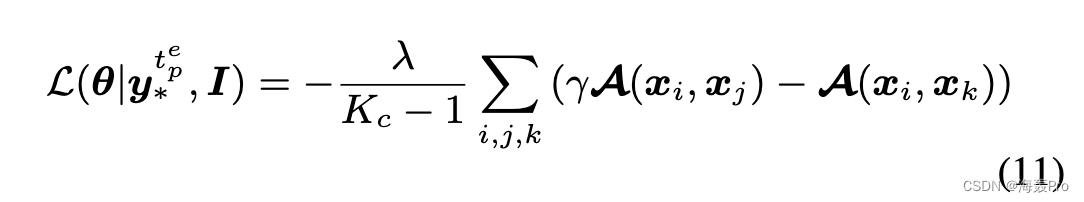
其中 γ 是一个权重，其值取决于 λ’ 以及在前向传播期间集群如何合并。 xi 和 xjare 来自同一簇，而 xk 来自相邻簇，它们的簇标签仅由最终的聚类结果 yte p∗ 确定。为了进一步简化优化，我们改为在训练批次中的其他集群中最多搜索 Kc 个 xi 的相邻样本中的 xk。因此，可以使用传统的随机梯度下降法来执行批量优化。请注意，这种三元组损失已经出现在其他作品中 [45, 54]。因为它与权重相关，所以我们称 (11) 加权三元组损失。