每日一读Large Scale Network Embedding: A Separable Approach

Posted 2022-12-15 海轰Pro

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了每日一读Large Scale Network Embedding: A Separable Approach相关的知识，希望对你有一定的参考价值。

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

唯有努力💪

【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/9117196

会议： IEEE Transactions on Knowledge and Data Engineering （CCF A类）

年度：2020年6月15日（发表日期）

Abstract

已经提出了许多成功的方法来学习大规模网络上的低维表示，而几乎所有现有的方法都是在不可分割的过程中设计的，即使只有一小部分节点是感兴趣的，也可以学习整个网络的嵌入。

这导致了极大的不便，特别是在大规模或动态网络上，这些方法几乎不可能实现。

在本文中，我们形式化了分离矩阵分解的问题，在此基础上，我们阐述了一个新的目标函数，它同时保留了局部和全局信息。

我们将我们的 SMF 框架与近似 SVD 算法进行比较，并证明 SMF 在分解给定矩阵时可以捕获更多信息。

我们进一步提出了 SepNE，这是一种简单灵活的网络嵌入算法，它独立地学习分离过程中不同节点子集的表示。通过实现可分离性，我们的算法减少了嵌入不相关节点的冗余工作，从而为大型网络提供了可扩展性。为了进一步将复杂信息整合到 SepNE 中，我们讨论了几种可用于在大型网络中利用高阶邻近度的方法。我们证明了 SepNE 在具有不同规模和主题的几个真实世界网络上的有效性。具有相当的准确性，我们的方法在大型网络上的运行时间显着优于最先进的基线。

1 I NTRODUCTION

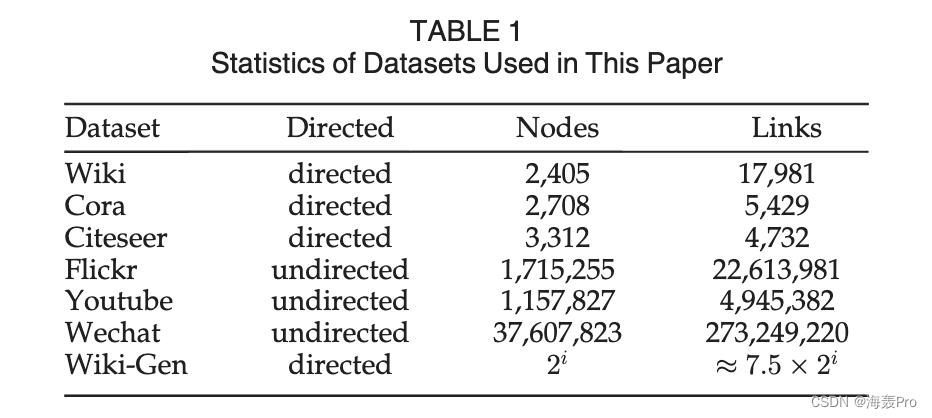
学习网络数据的低维表示或网络嵌入（NE）是大型网络上的一项具有挑战性的任务，其规模可以达到十亿级并且正在迅速增长。例如，Facebook 的月活跃用户数达到 22.3 亿，每年增长 11%。 1 同时，虽然网络的规模可能会随着数据的积累而无限增长，但通常只有一小部分节点对下游应用程序感兴趣。这就是**本文的出发点：我们能否分别学习不同节点子集的表示——与集体相比非常小——同时保留整个网络的信息？**如果是这样，我们可以为所请求的节点获得良好的表示，而无需多余的努力来嵌入不相关的节点。

效率是当代 NE 研究的一个主要方面，并且已经提出了各种适用于大规模网络的方法 [1]、[2]、[3]。几乎所有这些方法都将整个网络嵌入了不可分割的过程，其中一个节点的表示取决于每个其他节点的表示结果。在这个框架下可以实现全局定义的最优，同时也带来很大的不便：这些方法可以处理的最大网络大小最终是有限的。例如，最快的算法之一 LINE [2] 需要几个小时才能嵌入百万级网络。可能要花费数千小时才能在十亿级网络上实现同等性能。另一种方法以归纳方式学习模型，并对看不见的数据进行推断 [4]。这些模型具有方便的推理过程，但它们不能随时间变化，并且依赖大量的训练数据和时间来实现良好的性能。

大规模网络上的效率问题无法直接解决，因为算法的运行时间不可避免地与问题规模成正比增长。因此，我们提出了解决效率问题的新视角：可分离性。算法的可分离性表示不同工作人员在不交换信息和合并输出的情况下执行的能力。简单来说，可分离算法将原始问题分成不同的自立子问题并分别求解，子问题的解决方案是直接可用的答案，而不是中间结果。由于网络自然由节点及其关系组成，设计可分离 NE 算法的本能方法是将整个节点集划分为小的子集，并可分离地嵌入每个集。子问题的解决方案产生直接意义，作为相应节点集的表示。

在本文中，我们在基于矩阵分解的框架下实现了 NE 问题的可分离性。我们形式化了分离矩阵分解 (SMF) 的问题，并阐述了一种新颖的损失函数，该函数保留了局部、全局和地标级别的矩阵信息。然后，我们提出了分离网络嵌入（SepNE），一种基于 SMF 的可分离 NE 方法。图 1 说明了 SepNE 与现有方法的主要区别。 SepNE 首先将节点集划分为小的子集。然后建立一个特殊的地标集作为分区子集的参考以实现可比性，即不同集的表示位于相同的线性空间中。嵌入地标后，从 SMF 中定义的目标函数导出不同子集的表示。

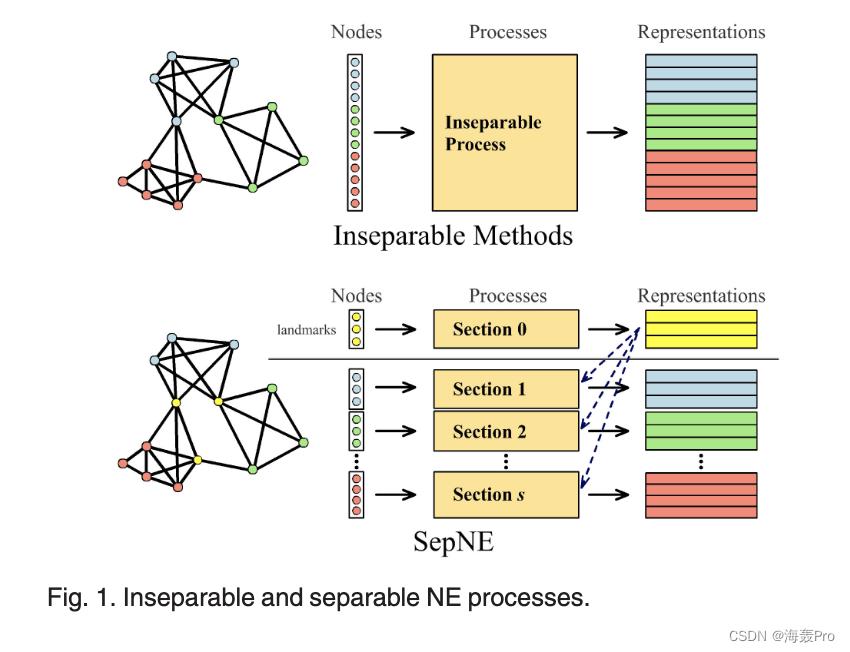
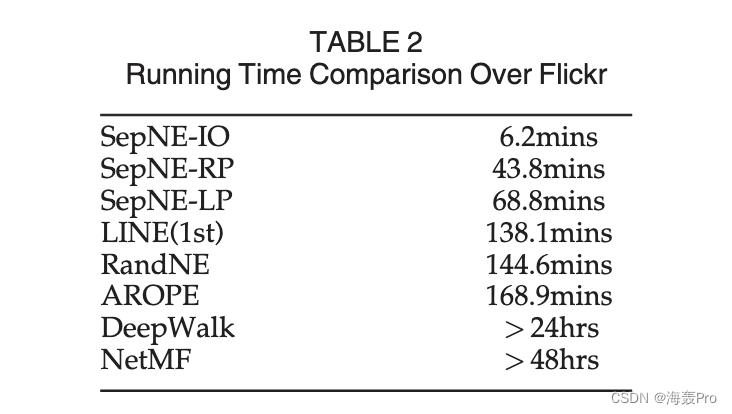
NE 问题中的可分离性产生了几个特定的优点。首先，可分离性使得它可以仅嵌入请求的节点，从而减少了嵌入不相关节点的徒劳努力；此外，SepNE 的优化复杂度仅与请求节点的数量有关，而不是与整个网络规模有关，从而导致对大型网络的可扩展性。其次，即使请求整个网络，SepNE 由于其简单性而显示出比最先进算法更高的速度，同时产生相当的准确性。第三，可分离性导致并行和分布式计算的自动和有效实现。

为了进一步说明我们的 SMF 框架，我们将其与 Nystrom 方法 [5] 进行比较，这是一种常用的近似 SVD 算法。 SMF 保留局部、全局和界标信息，而 Nystrom 仅在分解给定矩阵时保留界标信息，因此 SMF 具有更好的性能但 Nystrom 更快。为了在不损失效率的情况下将更复杂的信息整合到框架中，我们讨论了网络嵌入中的高阶近似，并总结了可以与 SepNE 结合以利用高阶信息的不同方法（包括 AROPE [6] 和 NEU [7]）在大型网络中。我们使用不同规模和主题的真实网络评估了 SepNE。与当前的 NE 方法（包括 DeepWalk [1] 和 LINE）相比，SepNE 具有同等或更高的准确度，至少快 50%。结果还显示了高阶近似在大规模网络中的有效性。

本文可能更重要的贡献是 SMF 的推广。 SMF 保持出色的性能，将 MF 问题的复杂性从三次降低到几乎线性。这导致在基于 MF 的算法的大量集合中有趣的进一步应用。

我们的贡献可以总结如下：

我们提供了评估网络嵌入方法的新视角：可分离性，这也是解决效率问题的新视角。我们在基于矩阵分解的框架下实现了 NE 问题的可分离性，并提出了 SepNE，一种可分离的 NE 方法。
我们提出了 SMF 框架并阐述了一种新颖的损失函数，可以在不同层次上保留矩阵信息。凭借出色的性能，SMF 将 MF 问题的复杂性从三次降低到几乎线性。 SMF 还可以推广到其他基于 MF 的算法，大大提高这些算法的效率。
我们总结了几种可以与 SepNE 结合以在大规模网络中结合高阶邻近信息的方法，并通过在不同网络数据集上的实验结果证明了高阶邻近在网络嵌入中的有效性。
我们用不同规模和主题的真实网络评估 SepNE，并将其与 DeepWalk 和 LINE 进行比较。结果表明，SepNE 比最先进的网络嵌入方法至少快 50%，具有同等或更高的准确性。

2 S EPARATED M ATRIX FACTORIZATION

2.1 Preliminaries

给定一个矩阵 M，矩阵分解 (MF) 旨在找到两个矩阵 W 和 C，它们都满足给定的约束并最小化重构 M 的残差~M 1/4 W T C。在公式中表示，我们有

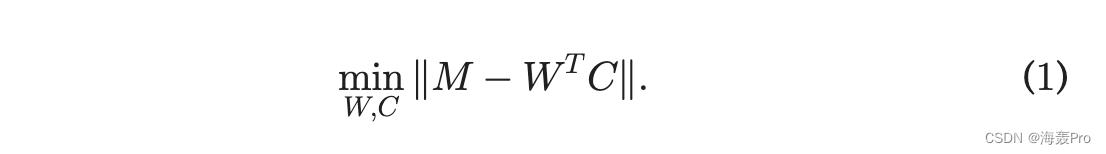
W; C 的秩低于 M。在 nn 节点网络的嵌入任务中，M 的大小为 ðn nÞ，其中每个条目表示两个对应节点之间的接近度。可以在各种度量中定义接近度，例如节点之间的边权重。 W 中的列是所需的表示。当被视为上下文时，C 中的列被解释为节点的表示。

最常用的矩阵分解方法之一是奇异值分解 (SVD)。对于矩阵 A 2 Rm n，SVD 给出 A 1/4 USV T ，其中 U 1/4 ðu1； u2; . . . ; u mÞ 2 Rm m 和 V 1/4 ðv1; v2; . . . ; v nÞ 2 Rn n 是正交矩阵。列向量 u i 是 A 的左奇异向量，向量 v i 是右奇异向量。对角矩阵 S 1/4 diagfs1; s2; . . . ; s rg 2 Rm n 由矩阵 A 的奇异值组成，其中 r 1/4 minfm； ng，我们有1 s2 s r 0。从SVD的形式可以看出，矩阵A的主成分是由较大的奇异值和对应的奇异向量决定的。因此我们可以保留前 d 个最大的奇异值并获得矩阵 A 的 rank-d 近似值。如果 d r 1/4 rankðAÞ 并且我们定义

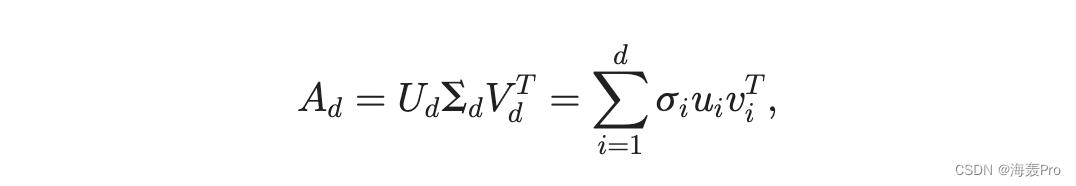
那么当用 Frobenius 范数和谱范数测量时，A 与 A 的任何 rank-d 近似值之间的差异被 Ad 最小化。2 在嵌入任务中，如果我们使用 SVD 来获得邻近矩阵 M 的最佳 rank-d 近似值，即 M d 1/4 UdSd V T d ，我们定义

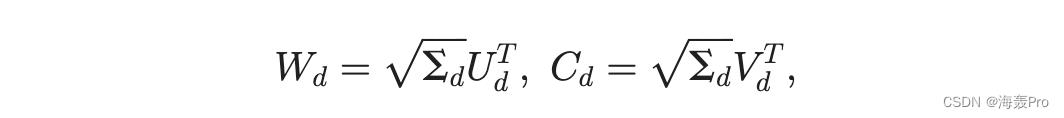
那么 Md 1/4 W T d Cd 和矩阵 W d 和 C d 是所需的 d 维表示。使用问题方程式的形式。 (1)，表示可以写成

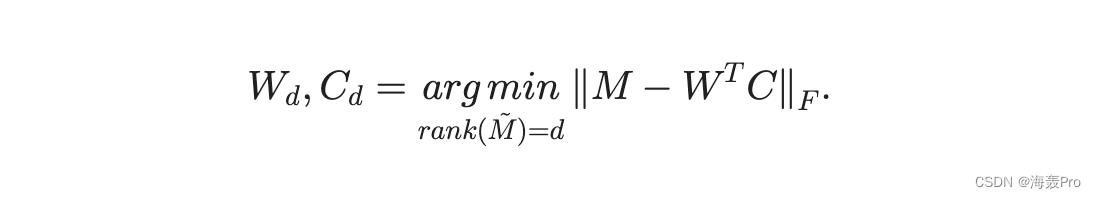
由于不可接受的时间复杂度，SVD 无法扩展到大型矩阵。因此，已经提出了许多近似方法作为节省时间的替代方法，其中一种方法是受到积分方程理论 [5]、[8] 中的 Nystrom 方法的启发。在本文中，我们也将其称为 Nystrom 方法，作为近似 SVD 方法的代表。 Drineas 等人提出的 LinearTimeSVD 算法。 [8] 通过随机选择 A 的 c n 列来构造矩阵 L 2 Rm c，然后计算 A 的 top-d 奇异值和对应的左奇异向量的近似值，然后计算 A 的 top-d 奇异值和对应的左奇异向量L 被认为是 A 的近似值。L 的奇异值和左奇异向量的计算是通过 c c 矩阵 LT L 的特征分解来执行的。 Drineas 等人。 [5] 进一步利用这个思想，通过形式来逼近 ann n Gram 矩阵 G

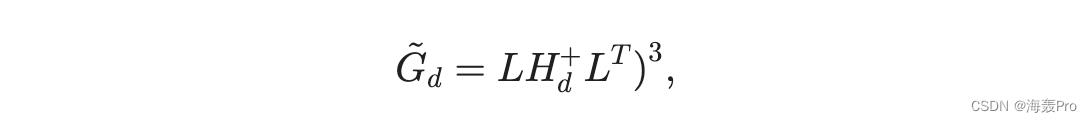
其中 L 的定义与之前相同，H d 是 H 的最佳 rank-d 近似值，由 L 中选择的 c 列与 G 的相应 c 行之间的交集形成的矩阵。证明通过选择 Oðd= 4Þ列

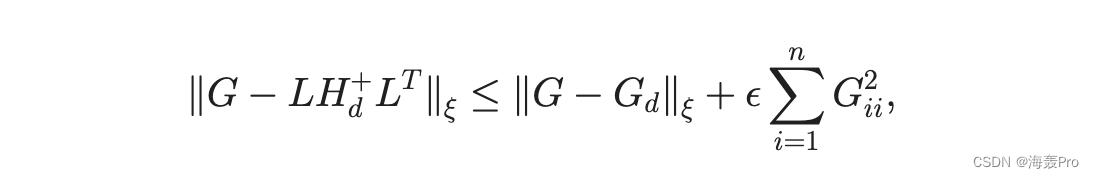
1/4 2 的预期和高概率；扇出所有 d rank(H) [5]。 Nystrom 的残差有一个相当好的上限。

2.2 Problem Definition

直接分解大规模网络的矩阵可能是不可接受的时间成本。因此，我们提出 SMF，一个新的优化问题，作为速度和准确性之间的权衡。为了实现可分离性，SMF 在节点集上划分问题，并相应地划分邻近矩阵。以下是 NE 场景中分离矩阵分解 (SMF) 的正式定义。

SMF 取一个网络 G 1/4 ðV； Þ; jV j 1/4 n，它的邻近矩阵 M，以及一个分区设置 f : V 7 ！ V, V 1/4 fV1; . . . ; Vsgas 输入。任务是导出表示 W 1/4 ðW1； . . . ; WsÞ 和 C 1/4 ðC1; . . . ; C sÞ 用于优化重构 M 的分区集。不失一般性，我们根据 V 置换和分区 M 为

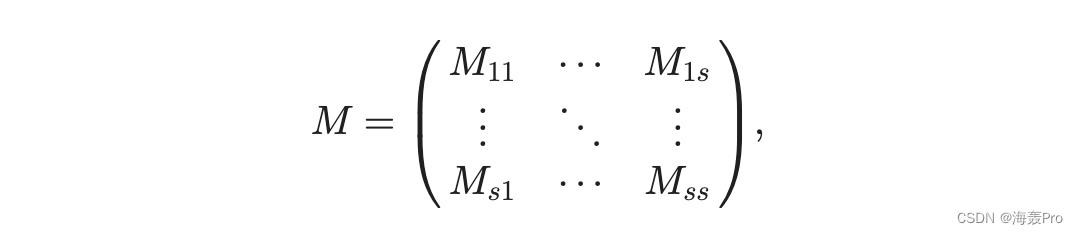
其中 M ij 表示 Vi 和 V j 之间的接近度。对应的重构矩阵~M为

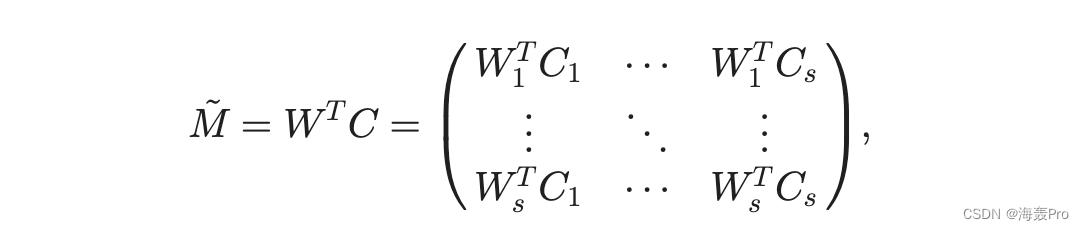
在 1/4 W T i Cj 中具有 ~M 的形式。重建的损失定义与问题（1）相同，即 kM ~MkF 。 4

为了实现部分之间的独立性，SMF 限制每个集合的嵌入部分 (i) 仅使用与其自身相关的邻近度进行 (嵌入 Vi 的部分只能利用 M ij 和 Mji, j 1/4 1; . . . ; s) 和 (ii) 没有其他部分的任何结果。

2.3 Method

对节点进行分区是实现可分离性的第一步。然而，由于对接近访问的限制，分区集中的表示可能是无法比较的。换句话说，不同集合的表示没有统一的约束将它们限制在相同的线性空间中。为了实现可比性，我们在网络中建立具有高度交互节点的地标，作为不同子集的不变参考。对于分解过程，仅保留局部信息是一种在丢失全局参考的情况下重建网络微观结构的简单方法。结合地标解决了可比性问题，但仍然忽略了不同子集之间的交互。因此，如图 2 所示，我们为 SMF 制定了一种新颖的目标函数，它保留了局部、全局和地标信息，从而实现了最先进的性能。

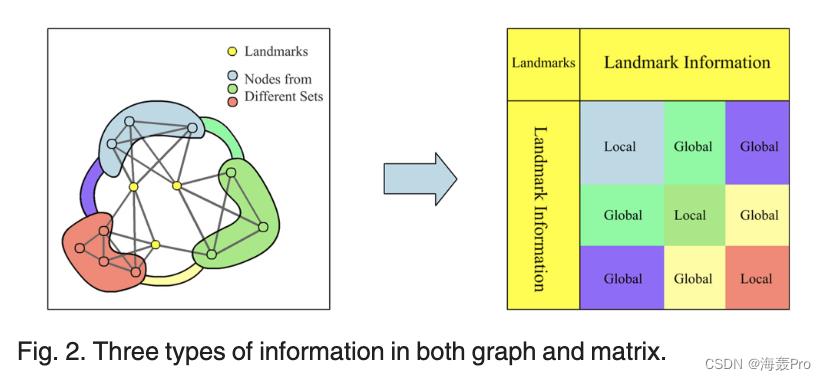
2.3.1 Local Information

划分矩阵中的邻近度自然分为两种，即局部信息和全局信息。局部信息是指每个集合内的邻近度，或对角线上的子矩阵；全局信息是指所有不同集合对或非对角子矩阵之间的接近度。我们开始用一个朴素的简化来建模 SMF，它通过分解对角线上的 s 个矩阵来仅保留局部信息

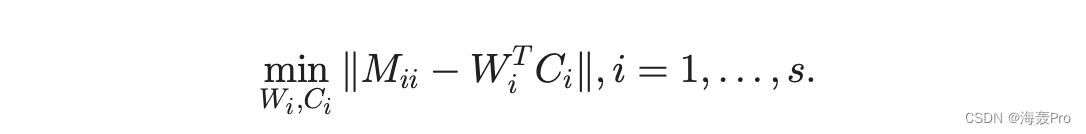
这种原始方法丢弃了不同集合之间的所有交互，导致无法比较的表示。

2.3.2 Landmark Information

为了实现可比性，我们求助于第三种信息，地标信息。地标信息指示子集和手动建立的地标之间的接近度，这是一组特殊的节点（表示为 V0），被选为不同子集的参考。改进的方法对不同集合中的地标信息设置统一约束，并分两个阶段解决问题，公式为

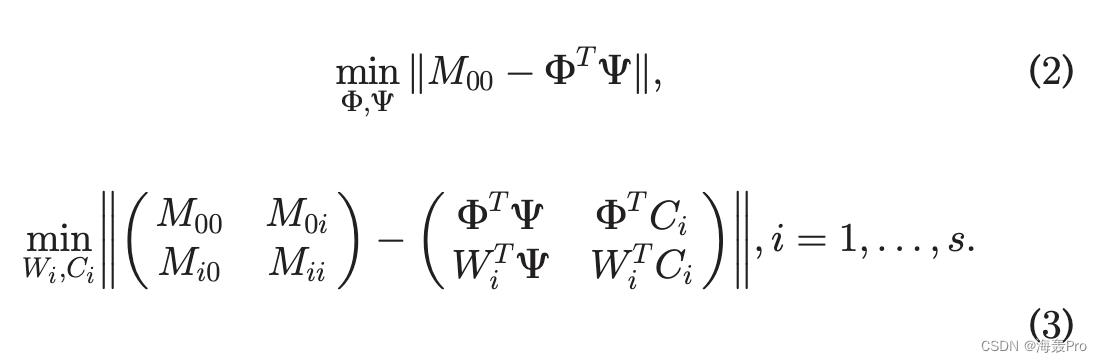
第一阶段在问题 (2) 中嵌入地标 (W0 1/4 F, C0 1/4 C)，第二阶段通过使用计算的 F 和 C 解决问题 (3) 来导出静止集的表示。如果使用 Frobenius 形式，问题 (3) 中的损失可以显式分解为局部损失和界标损失：

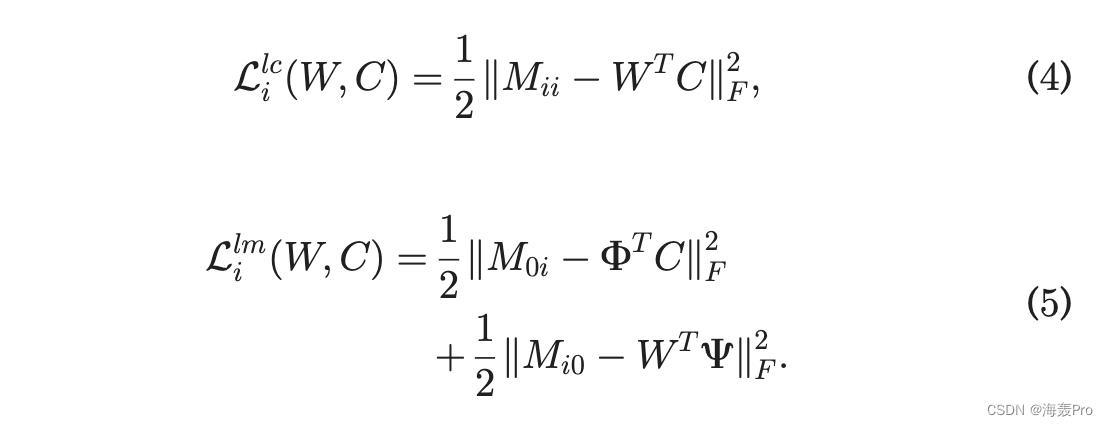
2.3.3 Global Information

为了进一步将全局信息结合到目标函数中，我们首先将问题 (3) 转换为等价形式来详细说明全局损失。我们表示 k :1/4 jV0j 并假设计算出的 F； C 2 Rd k 的等级为 d.5 W i ； Ci 2 Rd jVij 可以表示为列 inF 的线性组合； C，以矩阵表示形式表示为

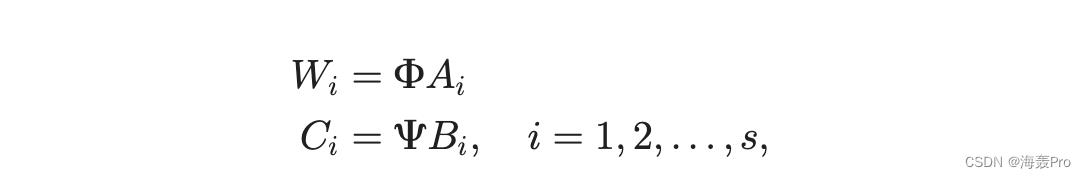
其中艾; Bi 2 Rk jV ij 是系数矩阵。通过这种方式，不同子集的表示被限制在由地标表示确定的相同向量空间中，因此我们实现了可比性

首先，我们考虑一个简单的情况，其中 s 1/4 2，V0 是地标集，V1 是要嵌入的目标子集。转换后，全局信息通过

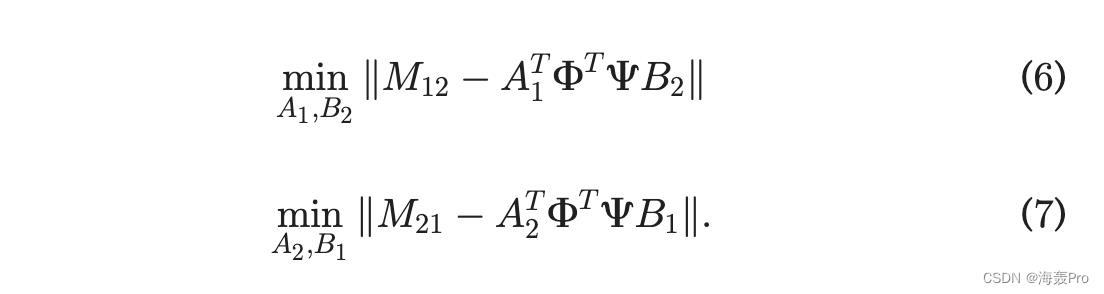
问题 (6)(7) 不可分，因为 V1 问题中存在嵌入 V2 (A2; B2) 的结果。然而，转换后出现了一个令人惊讶的性质，如果需要 V2 的表示来保存地标信息，则 FT CB2 1/4W T0 C2 1/4 ~M02 可以很好地近似于 M02，AT2 FT C 类似。因此，问题 (6)(7) 可以代入为

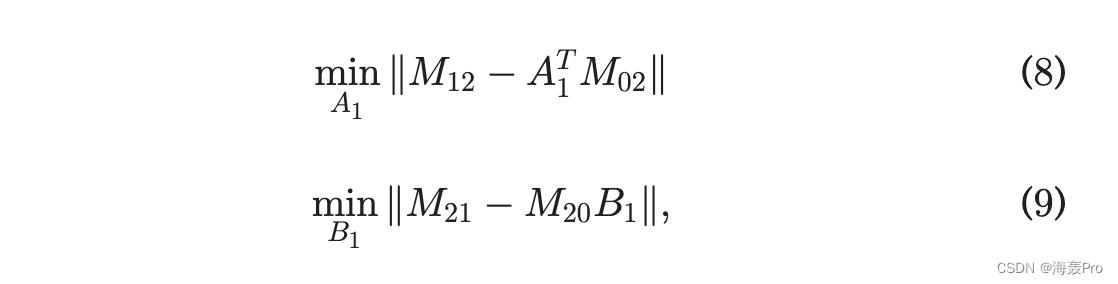
并实现了可分离性。

通过简单地将所有与 V2 相关的变量替换为与 V i 相关的变量，该想法可以推广到任何给定的 s 和 Vi，其中 V i 1/4 Sj =2 f0;igVj。对于一般情况，目标子集 V i 的全局信息通过

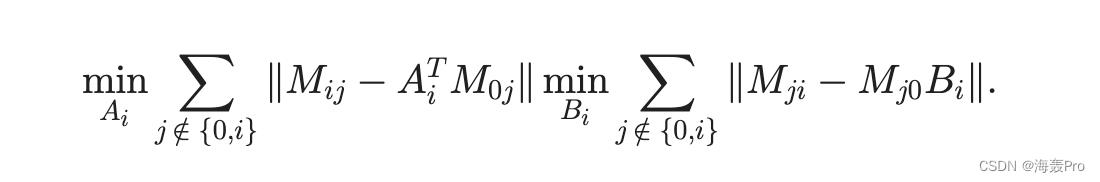
如果在所有集合中都保留了地标信息，则该近似值仍然成立。如果采用 Frobenius 范数，我们注意到

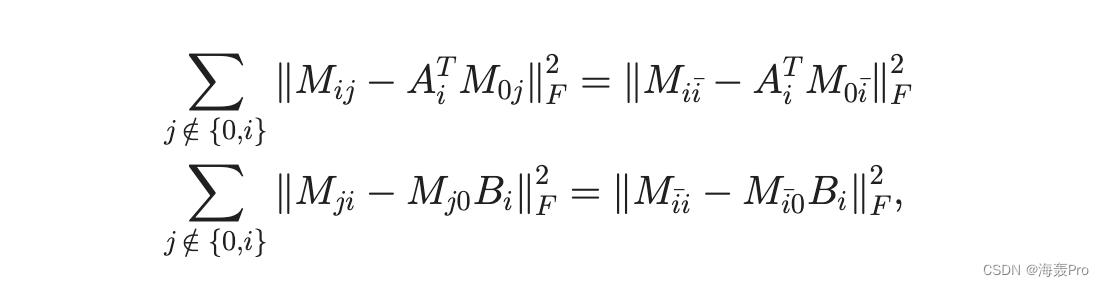
其中M i i 表示V i 和V i、M0 i、M ii 和M i0 之间的相似度。对于任何集合 Vi，全局损失函数定义为

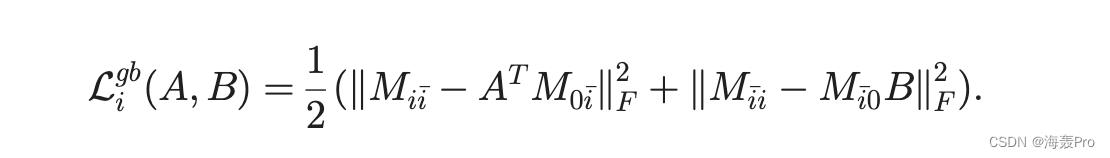
2.4 Final Optimization Problem

结合 -scaled 全局损失和正则化 overA； B、SMF的最终损失函数变为

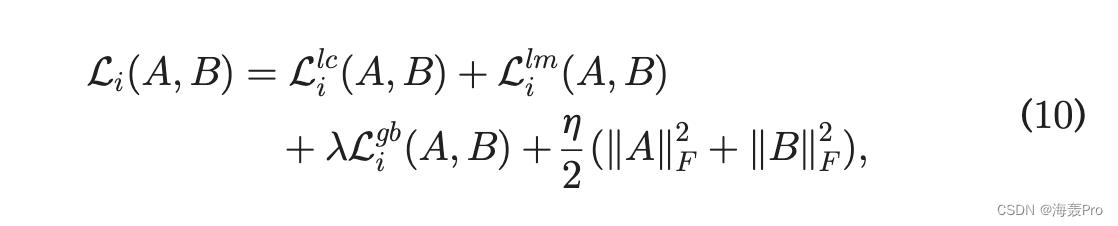
其中 Llc i 和 Llm i 在 A 中重新定义； B-表示，即

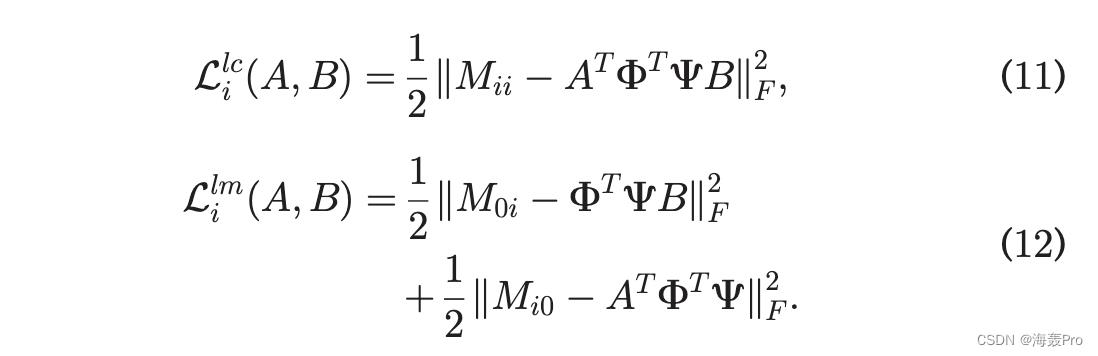
因此，SMF的最终优化问题被表述为

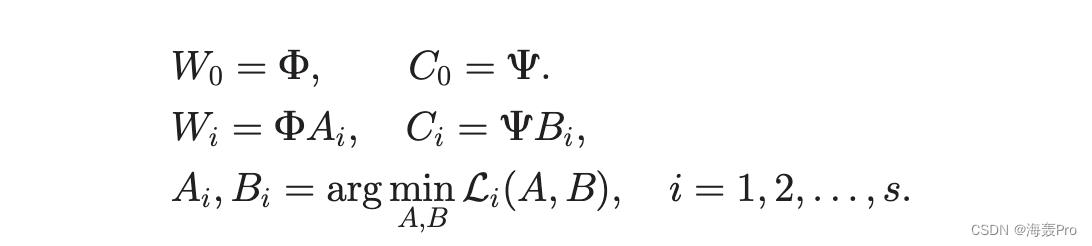
2.5 Relationship to the Nystr€om Method

Nystrom 方法 [5] 普遍用于获得给定矩阵的低秩逼近。为了进一步说明我们的 SMF 模型，我们将其与 Nystrom 进行比较，并在本节中解释这两种方法之间的关系。

Nystrom 要求 G 是一个对称正半定 (SPSD) 矩阵，但它可以推广到分解任何矩阵 M 2 Rn n。令 L 2 Rn c 是由 M 的选定 c 列形成的矩阵，R 2 Rc n 是由相应 c 行组成的矩阵。请注意，如果没有 SPSD，则 R 1/4 LT。 H 2 Rc c 由这些 c 列和 c 行相交形成。 Nystrom 方法给出了

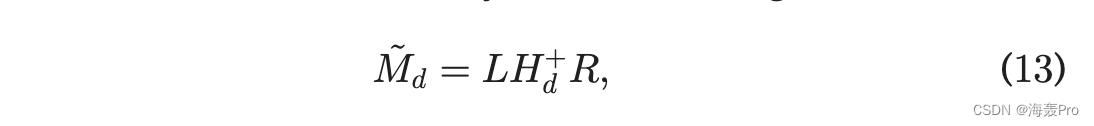
其中 Hþd 是 H 的最佳秩 d 近似的 Moore-Penrose 广义逆。如果 Hd 1/4 UdSd V T d ，则 Hþd 1/4 V dS 1d U T d 和 ~Md 1/4 LðV dS 1d U T d ÞR 1/4 ðLV dS 1d ÞSdðRT UdS 1d ÞT 。 Nystrom 方法给出了 M 的近似 SVD 是

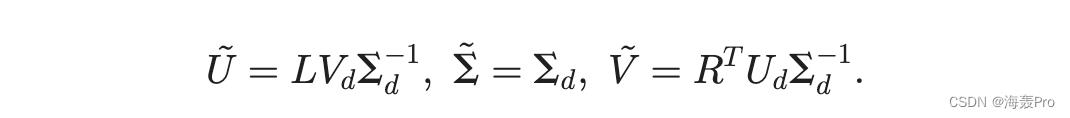
H的top-d奇异值被视为M的top-d奇异值的近似，L的左奇异向量被视为M的左奇异向量的近似，R的右奇异向量被视为作为 M 的右奇异向量。在计算 L 的左奇异向量时，Nystrom 也将 H 的奇异值和右奇异向量作为 L 的近似值，并直接具有 ~U 1/4 LV dS 1d 。 R 的右奇异向量的计算方法类似。

为了将 Nystr€om 方法与我们的 SMF 框架进行比较，首先我们将 M 重新排列和划分为

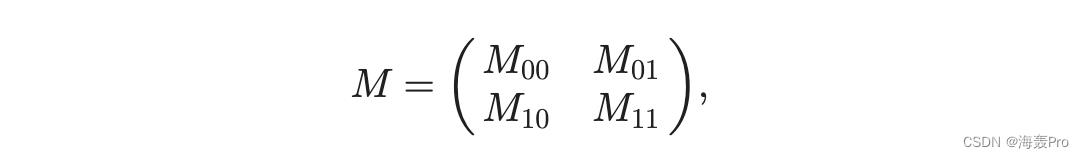
其中M的前c列是Nystrom中的那些列，前c行是对应的c行。M00 2 Rc c是这c列和c行的交集。

M10 2 Rðn cÞ c 是选择的 c 列和左侧 ðn cÞ 行的交集。 M01和M11的形成方式类似。根据 Nystrom 方法中矩阵 L、H 和 R 的定义，我们有

3 S EPNE: S EPARATED N ETWORK EMBEDDING

在本节中，我们提出了 SepNE，一种基于 SMF 的简单且可分离的 NE 方法。算法 1 给出了 SepNE 的一般框架。然后我们说明了 SepNE 的细节，包括分区设置、地标选择方法和优化方法。

SepNE 将给定的网络作为输入并输出节点表示。在准备阶段，选择并嵌入地标，并在一定的设置下划分剩余节点。在第二阶段，通过优化 SMF 问题独立嵌入分区集。第二阶段以可分离的方式设计，因此如果请求的节点比例很小，则算法1中的Loop 1只能在包含这些节点的集合上进行。此外，可分离性允许循环中的循环分布式运行。

对于要分解的邻近矩阵，SepNE 采用了两个度量。第一个度量定义了 M 1/4 A þ A2，其中 A 是 PageRank [9] 的转移矩阵。 8 第二个指标用 M 1/4 I + A 简化了第一个指标。我们的指标类似于 TADW [10]，它证明了分解 A 和 A + A2 和 DeepWalk [1] 之间的等效性，步行非常短。可以从邻近顺序的角度得出对指标的更本能的理解。 A 可以解释为一阶接近度的度量，而 A + A2 是一阶和二阶接近度的组合。 LINE [2] 中提出并进一步讨论了这些概念。

3.1 Partition Setups

我们在本文中为 SepNE 提出了三种不同的分区设置。 SepNE-LP（Louvain 分区）使用 Louvain [11] 根据其社区划分网络。利用社区结构使矩阵本地信息与网络本地信息相一致，9 这是提高性能的经验方法。

但是，由于 SepNE 利用了邻近矩阵的所有信息，因此不需要基于社区的分区。我们进一步提出了将节点随机分配给集合的 SepNE-RP（Random Patition），以及将请求的节点简单地放入一个或多个集合并忽略所有未请求的节点的 SepNE-IO（仅感兴趣）。

3.2 Landmark Selection

地标选择方法不仅影响地标的表示，还影响整个 SMF 问题中所有集合的丢失。由于设置界标的主要目的是为不同的集合建立参考，因此界标应该 (i) 与其余节点尽可能多的联系； (ii) 让连接覆盖尽可能多的组。

如果 k 控制松散，则选择具有高度数的节点的方法通常效果很好。然而，在现实世界的网络中，度数最高的节点往往分布在几个巨大且高度连接的社区中。当 k 被严格限制时，选择这些节点实际上限制了这些地标相邻的集合的数量。为了缓解这个问题，我们提出了贪婪支配集（GDS），一种贪婪地最大化地标相邻节点数量的方法。

GDS 首先使用节点的度数形成一个最大堆，并将地标集初始化为空。初始化后，GDS 反复检查堆顶。如果顶部与当前地标集中的至少一个节点相邻，则简单地删除它，否则将其添加到地标集中然后删除。该过程一直持续到堆为空或界标大小达到 k 为止。实验表明，当 k 受到严格限制时，GDS 可以很好地捕捉网络的信息结构。

在作为良好参考的同时，使用 GDS 选择的地标是完全一跳隔离的。因此，如果仅利用一跳邻近度，则 GDS 的 M00 应该是对角矩阵。此外，如果 k > d，SVD 将为某些地标生成空表示。因此，我们只在采用高阶邻近或 k 1/4 d 时才使用 GDS。否则，我们实施基于学位的方法。

5 E XPERIMENTS

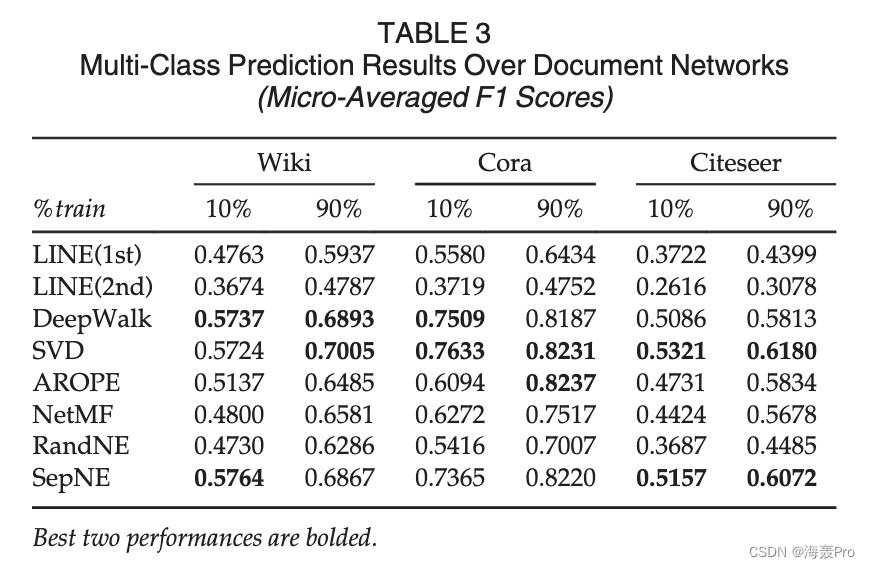
6 RELATED W ORK

有大量关于 NE 问题的文献提出。传统的降维方法 [17]、[18]、[19] 通过 Graph Laplacian Eigenmaps 或邻近 MF 适用于网络数据。最近，提出了各种基于skip-gram [20]、[21]的NE模型和应用[1]、[3]、[22]。此外，Levy 等人的开创性工作。 [23]证明了skip-gram模型和矩阵分解之间的等价性，这进一步导致了邻近MF框架下的新邻近度量[10]、[13]、[15]、[24]。在基于 MF 的算法中，AROPE [6] 和 NEU [7] 被提出将高阶信息合并到 NE 中，旨在更新通过任何其他 NE 方法获得的低阶嵌入以逼近高阶近似。提出了边缘重建算法 [2] 以在大型网络上获得可扩展性。神经网络，包括自动编码器 [25]、[26] 和 CNN [4]、[27]、[28] 也被用于 NE 问题。还有一种趋势[29]，[30]利用结构信息而不是接近度。

最近，已经为大规模网络提出了许多算法。 RandNE [16] 使用高斯随机投影而不是昂贵的优化来以分布式方式最小化矩阵分解问题。 GraphVite [31] 通过将通用网络嵌入框架分离到网络增强和嵌入训练阶段并将它们分别分配给 CPU 和 GPU 来构建带有 GPU 的嵌入系统。

上述方法中，DeepWalk[1]、LINE[2]和node2vec[3]适用于大规模网络，node2vec可以看作是DeepWalk的扩展，所以我们只比较了SepNE与DeepWalk和LINE。由于直接矩阵运算的复杂性，其他基于矩阵分解的方法，例如 GraRep [13] 和 NetMF [15]，无法扩展到大型网络。当节点特征可用时，GCN [27] 和 GraphSage [4] 运行良好，因此它们不适用于我们的问题。

与我们类似的作品有很多。在艾哈迈德等人。 [32]，采用了类似的分区来实现可分离性，而其他部分的工作与我们的工作有很大的不同。此外，它主要关注分布式学习中的技术问题，只保留链接信息，而 SepNE 是更广义的思想，具有更精细的优化目标。 P-GNN [33] 还对锚节点进行采样。然而，P-GNN 中的锚节点用于区分网络不同部分中具有相同局部结构的节点，方法是在一般 GNN 架构中添加关于锚集的距离，并且对锚节点进行多次重采样；而在 SepNE 中设置的界标是固定的，并用作底层嵌入空间的坐标。

7 C ONCLUSION

在本文中，我们形式化了分离矩阵分解的问题并提出了 SepNE，这是一种可分离的网络嵌入方法，在效率和性能上都优于强基线。我们进一步将我们的 SMF 框架与 Nystrom 方法（一种流行的近似 SVD 算法）进行比较，并证明 SMF 在分解给定矩阵时利用了更多信息，因此具有更好的性能。我们还使用 NEU 近似将高阶邻近信息合并到 SepNE 中，并展示其在网络嵌入中的有效性。

SepNE 的主要贡献是提供了评估网络嵌入方法的新视角：可分离性。可分离方法比可分配方法更强大，因为部分执行可分离任务提供了有意义的输出。该属性提供了仅嵌入一部分节点的选项，并在分布式学习、大规模网络嵌入中具有重要意义。至于未来的工作，矩阵重建损失下限的理论证明可以提供非常丰富的信息，从而在理论上将 SMF 应用于所有基于矩阵分解的算法。