单源最短路径—Bellman-Ford算法 Dijkstra算法

Posted 2022-12-15 之墨_

松弛操作

松弛操作就是判断从现在s到v的路径更近，还是我从s到u再到v更近，选一个更近的走。

松弛操作的例子

松弛是唯一导致最短路径估计和前驱结点变化的操作

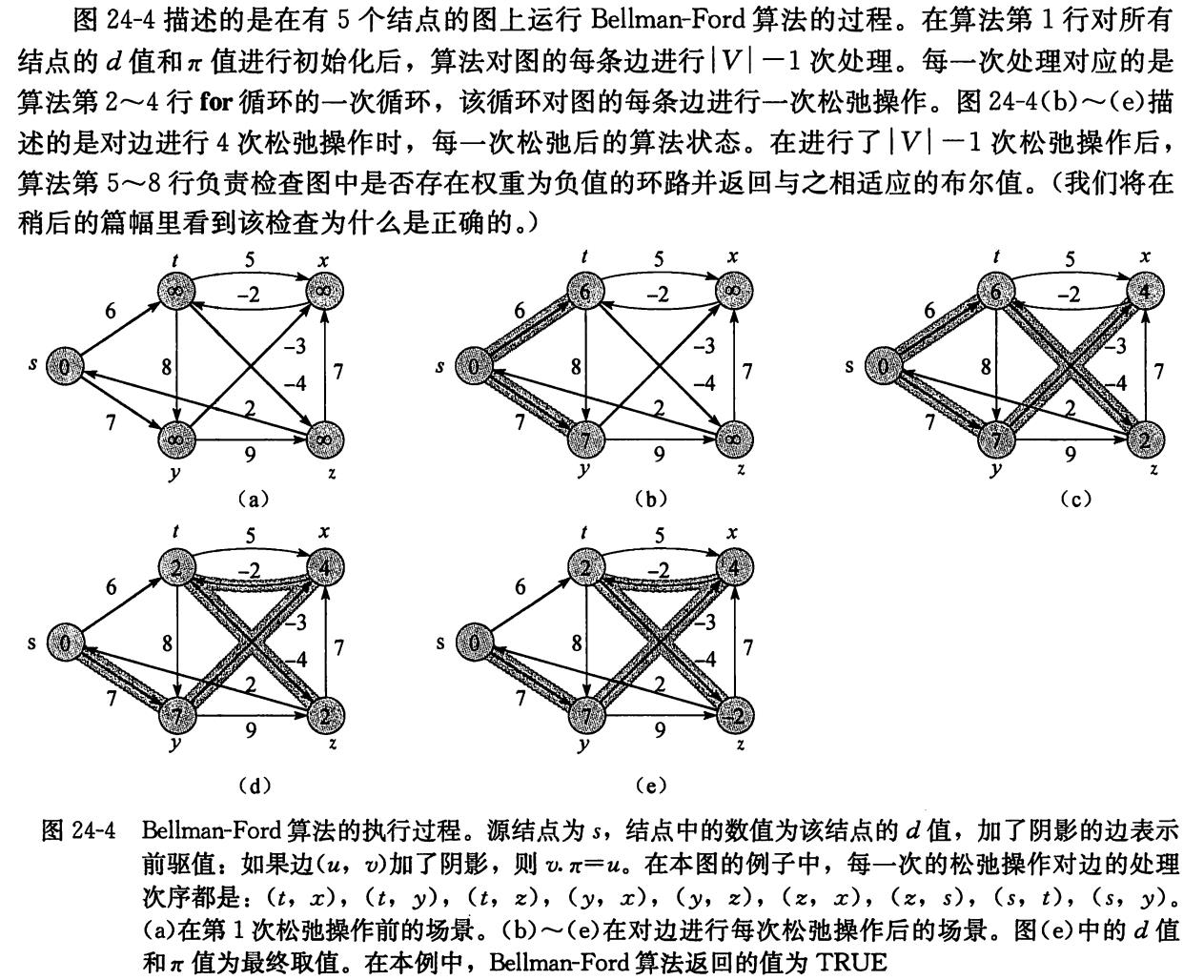
Bellman-Ford算法

第一个循环，循环V-1次，每次循环对所有的边都松弛一次，所以最终每条边都松弛了V-1次
最后对每条边再判断一下，如果每条路径都已经是最短了，就不会再出现从s到u到v比s到v更短的情况，因为前面的松弛就已经找出了这种情况，V-1次已经可以保证把所有可能都找完，而现在又出现这种情况，说明存在负环，只有存在负环才可以无限的把路径长度减小

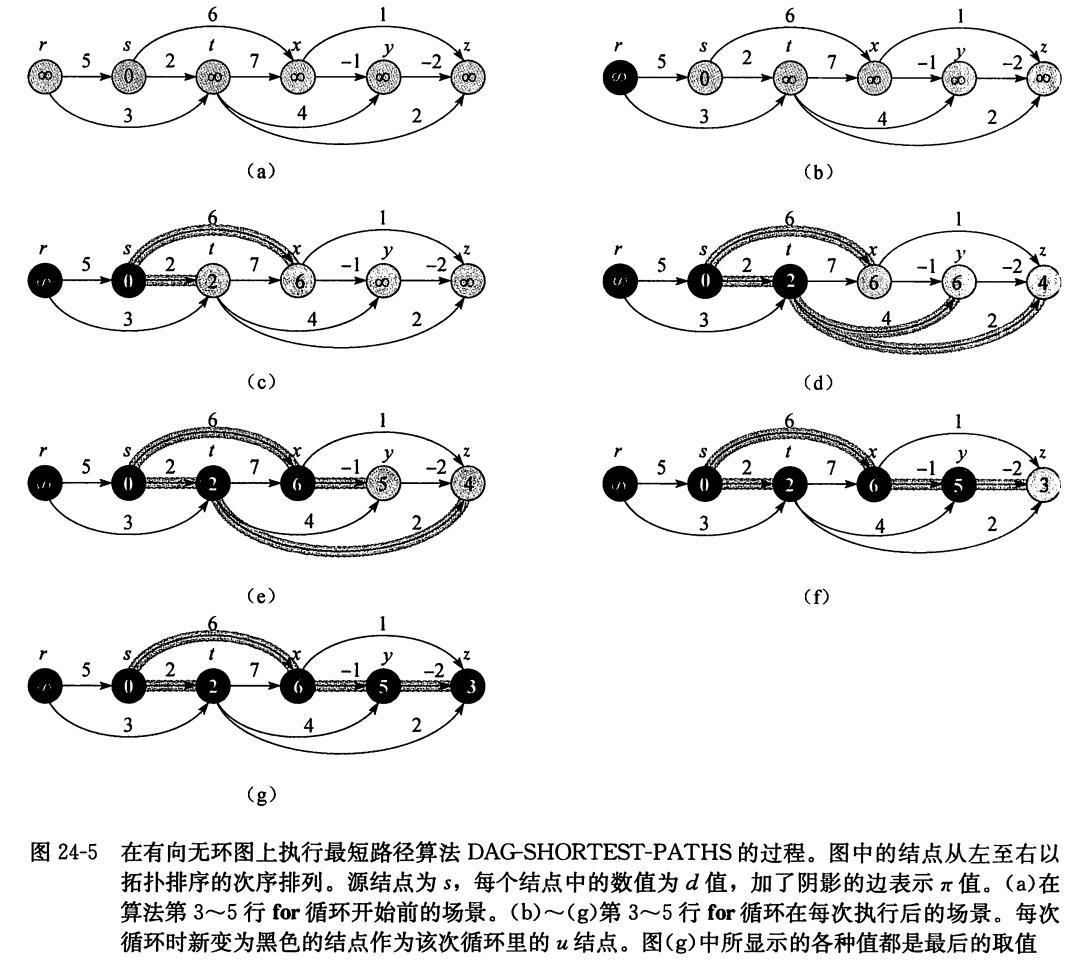
有向无环图的单源最短路径问题

Dijkstra算法

Dijkstra算法与Prim算法很像，Dijkstra算法是BFS的升级版，若要求最短路径由无权变为有权则BFS就不再适用，所以使用Dijkstra算法，故对于无权图，用Dijkstra算法其实就是BFS，因为Dijkstra算法每次选择集合V-S中“最轻”或“最近”的结点加入集合S中，该算法使用的是贪心策略，该算法每次选择结点u加入集合S时，有
Dijkstra算法像Prim算法的地方是，两个算法都使用最小优先队列来寻找给定集合(Dijkstra算法中的S集合与Prim算法中逐步增长的树)之外的“最轻”结点，将该结点加人到集合里，并对位于集合外面的结点的权重进行相应调整。