Machine Learning3.多元线性回归

Posted 2022-12-14 LiemZuvon

多元特征

线性问题中带有多个变量的问题称为“多元线性回归”问题。

假说函数

通式：h_theta(x) = theta_0+theta_1*x_1+theta_2*x_2+...+theta_n*x_n

向量化：h_theta(X) = X'Theta （这里令x_0=1）

向量化的技巧：两个矩阵相乘，维数需要对应。

开销函数

J(Theta) = SUMi = 1 -> i = m((h(X)-Y)^2)/(2*m)

多元的梯度递减

loop until convergence：

  Theta = Theta - alpha*SUMi = 1 -> i =m(X*(h(X)-Y))/m

由于多元下的梯度下降可能由于特征值得范围区别很大，导致下降速度很慢，因此我们可以考虑通过将特征的范围归一化，理想地有

-1 <= x_i <= 1 或者 -0.5<= x_i <=0.5

范围并没有特定的要求，只需满足特征之间的差距不要太大。两个方法可以帮助我们实现，特征放缩和均值归一化。特征放缩可以除以特征的取值范围，使特征值保持在[0,1]，利用(x_i-mu（x_i）)/range(x_i)使特征值保持在[-0.5, 0.5]或者（x_i-mu(x_i)）/Sigma(x_i)

可以通过利用导数的定义，利用某点前后两个很靠近的值除以他们的横坐标所得的值近似于该点的导数，从而验证之前的求得导数是否是正确的。

Normal Equation

Normal Equation 是一种不用迭代即可得到最优解的方法

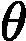
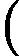
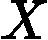
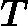
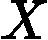
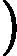
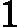
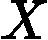
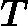
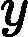
选择梯度下降还是Normal Equation的时机：

Gradient Descent	Normal Equation
Need to choose alpha	No need to choose alpha
Needs many iterations	No need to iterate
Works well when n is large	Slow if n is very large

吴恩达建议在n超过10000的时候应该考虑抛弃normal equation，因此一个10000*10000做求逆运算会很耗时

根据公式可知normal equation要求是
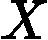
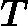
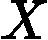可逆的，因此在用matlab或octave计算时，要采用pinv而非inv计算。

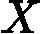
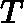
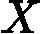 may be noninvertible. The common causes are:

• Redundant features, where two features are very closely related (i.e. they are linearly dependent)
• Too many features (e.g.  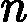). In this case, delete some features or use "regularization" (to be explained in a later lesson).

参考：https://share.coursera.org/wiki/index.php/ML:Linear_Regression_with_Multiple_Variables