tensorflow学习-------激活函数（activation function)

Posted 2022-12-14 岳飞传

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了tensorflow学习-------激活函数（activation function)相关的知识，希望对你有一定的参考价值。

1. 激活函数
2.激活函数的分类：
3.激活函数选择

tensorflow学习——-激活函数（activation function)

1. 激活函数

激活函数（activation function)运行时激活神经网络中某一部分神经元，将激活信息向后传入下一层的神经网络。
神经网络之所以能解决非线性问题，本质上是激活函数加入了非线性因素，弥补了线性模型的表达能力，把“激活的神经元的特征”通过函数保留并映射到下一层。
神经网络的数学基础是处处可微，所以激活函数要能保证数据输入与输出也是可微的。
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数，那么该网络仅能够表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。因此也可以认为，只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习能力；
激活函数应该具备的性质：

可微性：当优化方法是基于梯度的时候，这个性质是必须的。
单调性：当激活函数是单调的时候，单层网络能够保证是凸函数。
输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著;当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的learning rate

激活函数不会更改输入数据的维度，激活函数在Tensorflow的神经网络模块（Neural Network),即tf.nn模块

2.激活函数的分类：

2.1非线性激活函数

sigmoid
tanh
elu
softplus
softsign

2.1.1 sigmoid函数

函数定义

$f(x) = \\frac11+e^-x$
函数图像：

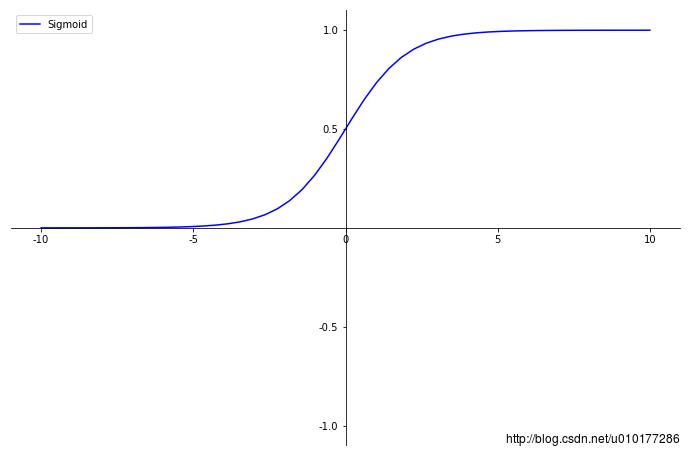
sigmoid 是使用范围最广的一类激活函数，具有指数函数形状，它在物理意义上最为接近生物神经元。此外，(0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数。
然而，sigmoid也有其自身的缺陷，最明显的就是饱和性。从上图可以看到，其两侧导数逐渐趋近于0

limx→∞f'(x)=0 lim x → ∞ f ′ ( x ) = 0 $\\lim_x\\to ∞f′(x)=0$

具有这种性质的称为软饱和激活函数。具体的，饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和, 即

f'(x)=0，当|x|>c，其中c为常数 f ′ ( x ) = 0 ，当 | x | > c ，其中 c 为常数 $f′(x)=0，当|x|>c，其中c为常数$

sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个 f′(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f′(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象
此外，sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

2.1.2 tanh函数

函数定义：

tanh(x)=1−e−2x1+e−2x t a n h ( x ) = 1 − e − 2 x 1 + e − 2 x $tanh(x) = \\frac1-e^-2x1+e^-2x$
函数图像

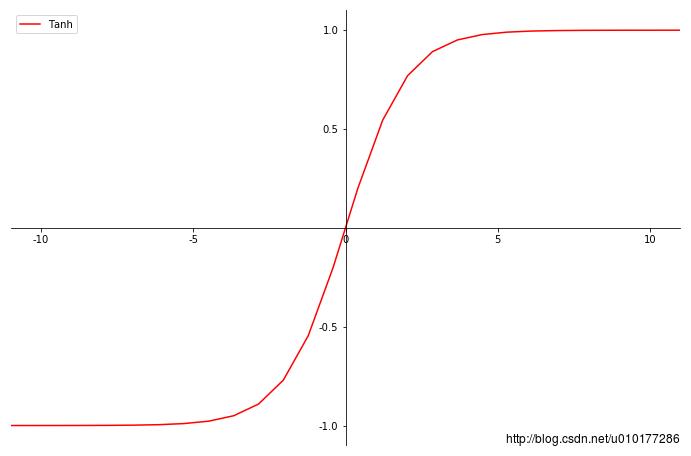
tanh函数也具有软饱和性。因为它的输出以0为中心，收敛速度比sigmoid更快。但是仍无法解决 梯度消失的问题；

2.1.3 函数曲线绘制代码

# -*- coding: utf-8 -*-
"""
Created on Tue Mar  6 22:18:40 2018

@author: spfhy
"""
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['axes.unicode_minus'] = False

def sigmod(x):
    return 1.0/(1.0+np.exp(-x))

fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)

x = np.linspace(-10,10)
y = sigmod(x)
tanh = 2*sigmod(2*x) - 1

plt.xlim(-11,11)
plt.ylim(-1.1,1.1)

ax.spines['top'].set_color('none')  
ax.spines['right'].set_color('none')  

ax.xaxis.set_ticks_position('bottom')  
ax.spines['bottom'].set_position(('data',0))  
ax.set_xticks([-10,-5,0,5,10])  
ax.yaxis.set_ticks_position('left')  
ax.spines['left'].set_position(('data',0))  
ax.set_yticks([-1,-0.5,0.5,1])  

plt.plot(x,y,label="Sigmoid",color = "blue") 
plt.plot(2*x,tanh,label="Tanh", color = "red")  
plt.legend()  
plt.show()

函数曲线比较：

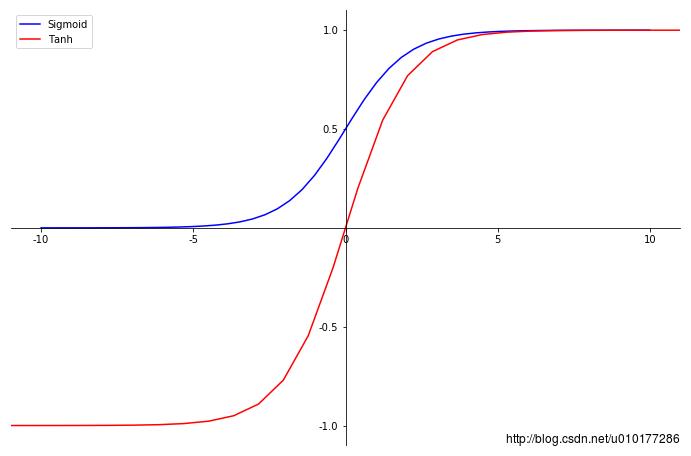
2.2 连续但不是处处可微的函数：

relu
relu6
crelu
relu_x

2.2.1relu函数

relu函数是目前最受欢迎的激活函数，定义如下：

f(x)=max(x,0) f ( x ) = m a x ( x , 0 ) $f(x) = max(x,0)$
softplus可看作是relu 的平滑版本，其定义如下：

f(x)=log(1+exp(x)) f ( x ) = l o g ( 1 + e x p ( x ) ) $f(x) = log(1+exp(x))$
函数曲线图如下：

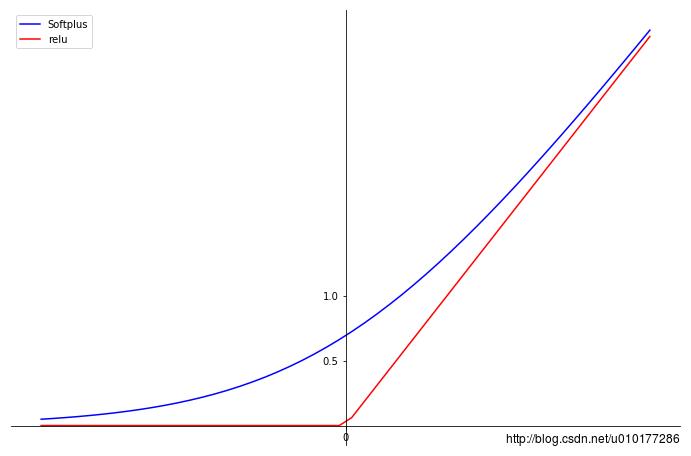
由图可见，relu在x<0 时硬饱和。由于x>0时，倒数为1，所以，relu能够在x>0时保持梯度不衰减，从而缓解梯度消失问题，还能够更快的收敛，并提供了 神经网络的稀疏表达能力( 如何理解？）。但是，随着训练的进行，部分输入会落到硬饱和区，导致对应的权重无法更新，称为“神经元死亡”。

2.2.2 函数曲线绘制代码

# -*- coding: utf-8 -*-
"""
Created on Tue Mar  6 23:43:09 2018

@author: spfhy
"""

# -*- coding: utf-8 -*-
"""
Created on Tue Mar  6 22:18:40 2018

@author: spfhy
"""
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['axes.unicode_minus'] = False

def softplus(x):
    return np.log(1+np.exp(x))

fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)

x = np.linspace(-3,3)
y = softplus(x)
relu = np.maximum(x,0)

#plt.xlim(-3,3)
#plt.ylim(-1.0,3.0)

ax.spines['top'].set_color('none')  
ax.spines['right'].set_color('none')  

ax.xaxis.set_ticks_position('bottom')  
ax.spines['bottom'].set_position(('data',0))  
ax.set_xticks([-10,-5,0,5,10])  
ax.yaxis.set_ticks_position('left')  
ax.spines['left'].set_position(('data',0))  
ax.set_yticks([-1,-0.5,0.5,1])  

plt.plot(x,y,label="Softplus",color = "blue") 
plt.plot(x,relu,label="relu", color = "red")  
plt.legend()  
plt.show()