基于参考点的非支配遗传算法-NSGA-III

Posted 2022-12-13 流浪若相惜

上一篇我们讲了有关非支配遗传算法NSGA-III的非约束过程，接下来这一篇我们讲一下NSGA-III约束实现以及扩展自适应方法。同理，我们先列一下我们参考的博客、代码以及论文。

文章目录

• • • 参考博客
    • 参考论文
    • 参考代码
    • NSGA-III约束实现
    • • Modifications in the Elitist Selection Operator
      • Modification in Creation of Offspring Population

参考博客

platEMO
基于参考点的非支配遗传算法-NSGA-III（一）

参考论文

因参考论文较多，此直接给予所有论文，请点击下载。论文中重要的部分已做了注解和标注。

1. Y. Tian, R. Cheng, X.Y. Zhang, and Y.C. Jin, “PlatEMO: A MATLAB platform for evolutionary multi‐objective optimization [educational forum],” IEEE Computational Intelligence Magazine, 2017, 12(4): 73‐87.
2. K. Deb, H. Jain . An Evolutionary Many-Objective Optimization Algorithm Using Reference Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601.
3. Y. Tian , X. Xiang , X. Zhang , et al. Sampling Reference Points on the Pareto Fronts of Benchmark Multi-Objective Optimization Problems[C]. 2018 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2018.
4. X. Zhang, Y. Tian, R. Cheng, and Y. Jin, “An efficient approach to nondominated sorting for evolutionary multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 2, pp. 201–213, Apr. 2015.
5. I. Das and J. Dennis, “Normal-boundary intersection: A new method
   for generating the Pareto surface in nonlinear multicriteria optimization
   problems,” SIAM J. Optimization, vol. 8, no. 3, pp. 631–657, 1998.
6. K. Deb, R.B. Agrawal, Simulated binary crossover for continuous search space, Complex Systems. 9 (1995) 115–148.
   在原有参考论文的基础上，本博客主要参考论文
7. H. Jain,K. Deb, A. Pratap, S. An Evolutionary Many-Objective Optimization Algorithm Using Reference-point Based Non-dominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach, IEEE Trans. Evol. Comput.,18(4):602-622, 2014.

参考代码

platEMO

NSGA-III约束实现

在NSGA-II中我们提到，我们是在划分等级的时候实现了考虑约束的多目标优化 (详细请参考：多目标非支配排序遗传算法-NSGA-II（一))，主要包括以下几种情况：

主要实现代码如下：

function domMat = calcDominationMatrix(nViol, violSum, obj)
% Function: domMat = calcDominationMatrix(nViol, violSum, obj)
% Description: Calculate the domination maxtrix which specified the domination
%   releation between two individual using constrained-domination.
%
% Return: 
%   domMat(N,N) : domination matrix
%       domMat(p,q)=1  : p dominates q
%       domMat(p,q)=-1 : q dominates p
%       domMat(p,q)=0  : non dominate
%
%    Copyright 2011 by LSSSSWC
%    Revision: 1.0  Data: 2011-07-13
%*************************************************************************

N       = size(obj, 1); %行个数（种群）
numObj  = size(obj, 2);% 列个数（目标函数）

domMat  = zeros(N, N); 

for p = 1:N-1
    for q = p+1:N
        %*************************************************************************
        % 1. p and q are both feasible
        %*************************************************************************
        %两个个体约束均为0的情况
        if(nViol(p) == 0 && nViol(q)==0) 
            pdomq = false;
            qdomp = false;
            for i = 1:numObj
                if( obj(p, i) < obj(q, i) )         % objective function is minimization!
                    pdomq = true; % p支配q
                elseif(obj(p, i) > obj(q, i))
                    qdomp = true;
                end
            end
    %只有两个对比个体所有目标函数都为1或0是才会产生支配，若存在不同目标函数个体支配相反情况，则两个个体不存在支配与被支配关系
            if( pdomq && ~qdomp )
                domMat(p, q) = 1; %表示p支配q
            elseif(~pdomq && qdomp )
                domMat(p, q) = -1; %表示q支配p
            end
        %*************************************************************************
        % 2. p is feasible, and q is infeasible
        %*************************************************************************
        elseif(nViol(p) == 0 && nViol(q)~=0)
            domMat(p, q) = 1;
        %*************************************************************************
        % 3. q is feasible, and p is infeasible
        %*************************************************************************
        elseif(nViol(p) ~= 0 && nViol(q)==0)
            domMat(p, q) = -1;
        %*************************************************************************
        % 4. p and q are both infeasible
        %*************************************************************************
        else
            if(violSum(p) < violSum(q))
                domMat(p, q) = 1;
            elseif(violSum(p) > violSum(q))
                domMat(p, q) = -1;
            end
        end
    end
end

在NSGA-II中实现此过程是在选择之前实现的，在NSGA-III约束实现时，其原理上是一样的只是在两个地方进行了修改，我这里直接截图原文，然后再每一部分具体解释一下。

Modifications in the Elitist Selection Operator

其实，我们在NSGA-II中也是采用了此思想，不同的是我们在NSGA-II中令违背约束的条件个数=0，而此采用的是
$$CV(\mathbf{x})＝\sum _{j=1}^J<{\overline{g}}_j(\mathbf{x})>+\sum _{k=1}^K|{\overline{h}}_k(\mathbf{x})|\text{\hspace{1em}(1)}$$其中，运算符的作用其实就是让$CV\ge 0$, 且让${\overline{g}}_j$变为$-{\overline{g}}_j$ 。我们在往下思考一下, $CV\ge 0$意味着什么？我们不妨列举一个test problem来说明此问题。例如C1_DTLZ1的约束为：
$$c(\mathbf{x})=1-\frac{f_M(\mathbf{x})}{0.6}-\sum _{i=1}^{M-1}\frac{f_i(\mathbf{x})}{0.5}\ge 0\text{\hspace{1em}(2)}$$按照文中所说，也就是让$c(\mathbf{x})\le 0$ ，那么（2）式转为：
$$-c(\mathbf{x})=\frac{f_M(\mathbf{x})}{0.6}+\sum _{i=1}^{M-1}\frac{f_i(\mathbf{x})}{0.5}-1\le 0\text{\hspace{1em}(3)}$$
（2）式跟（3）式所要表示的含义是一致的，但运算符$<>$操作后，会使得$CV\ge 0$，这与原有的constraints相反，也就说所谓的constraint violation含义。也就说在选择等操作所用的约束条件是违背的，也就是所谓的infeasible solution。

需要注意的是，文中的α已经是<>之后的了，运算符之后，feasible solution constraints 已经变为了<0, 也就是说将<0的约束（feasible 约束）的违背约束设置为0。

Modification in Creation of Offspring Population

其实，我们仅需要理解下边这段话就可以了：

意思就是说，我们之前仅在NSGA-II选择的划分等级时考虑了，但是并没有在父代生成子代中考虑这种支配关系，这样我们的整个过程如下伪代码：

代码实现：

 MatingPool = TournamentSelection(2,N,sum(max(0,PopCon),2));
 

function index = TournamentSelection(K,N,varargin)
    varargin = cellfun(@(S) reshape(S,[],1),varargin,'UniformOutput',false);% return by the form of cell type
    % For example
    %   A = cellfun(@(x) x(1:3),C,'UniformOutput',false)
    %   A = 1x5 cell
    %   'Mon'    'Tue'    'Wed'    'Thu'    'Fri'
    % reshape restruct array 
    [~,rank] = sortrows([varargin:]);%默认第一列排序,rank种群排列的索引位置
    [~,rank] = sort(rank);%升序排列，rank种群原要素的排序位置
    Parents  = randi(length(varargin1),K,N);%随机产生二元锦标赛个体
    [~,best] = min(rank(Parents),[],1);%按列排序
    index    = Parents(best+(0:N-1)*K);%种群个体索引位置
end

对于TournamentSelection（）我们可以这样去理解，这个函数是为了说明在父代生成子代过程时发生的，需要进行条件约束下的支配选择。这个函数的关键点就在于对$sum(max(0,PopCon),2)$ 的理解，它实则就是实现我们前边所说的运算符$<>$。我们前边也介绍了PopCon是符合约束的，那么对于feasible solution 这个操作的结果肯定是0，而对于infeasible solution来说肯定是sum(PopCon)。那么在进入函数二元锦标赛选择时，我们的排序是根据sum(PopCon)从小到大排序的，那么feasible solution肯定是在最前边的，也就是说feasible solution的 sum(PopCon)（约束违背）要小于infeasible solution的，对于两个feasible solution我们可以任一选择一个，对于两个infeasible solution来说谁的sum(PopCon)小，则优选谁。

function [FrontNo,MaxFNo] = NDSort(varargin)

    PopObj = varargin1;
    [N,M]  = size(PopObj);
    if nargin == 2
        nSort  = varargin2;
    else
        PopCon = varargin2;
        nSort  = varargin3;%reference points count
        Infeasible           = any(PopCon>0,2);%any one PopCon>0 will be a infeasible solution
        PopObj(Infeasible,:) = repmat(max(PopObj,[],1),sum(Infeasible),1) + repmat(sum(max(0,PopCon(Infeasible,:)),2),1,M);
        %不可行解一定obj一定是大于所有解的最大的，这样的就可以得到最小化问题中feasible solution obj一定小于
        %infeasible solution obj，然后对于两个feasible solution仅需对比obj，对于两个infeasible solution 仅需对比PopCon
    end
    if M < 5 || N < 500
        % Use efficient non-dominated sort with sequential search (ENS-SS)
        [FrontNo,MaxFNo] = ENS_SS(PopObj,nSort);

在选择过程中，重点理解

Infeasible           = any(PopCon>0,2);
PopObj(Infeasible,:) = repmat(max(PopObj,[],1),sum(Infeasible),1) + repmat(sum(max(0,PopCon(Infeasible,:)),2),1,M);

这两句的意思就可以实现feasible solution以及infeasible solution的所有组合情况，对于feasible 我们仍然是对于其目标函数的对比，对于infeasible solution我们可以通过sum(PopCon)，而对于feasible solution以及infeasible solution来讲，我们 $$PopObj(Infeasible,:)=repmat(max(PopObj,[],1),sum(Infeasible),1)+repmat(sum(max(0,PopCon(Infeasible,:)),2),1,M);$$就可以看出，infeasible solution即使再小，也是大于feasible solution中目标函数最大的那个（我们这里采用min function）,即任一一个infeasible solution的“目标函数值”要大于所有的feasible solution。这样我们就实现了父代生成子代、种群选择过程中的约束优选算法。
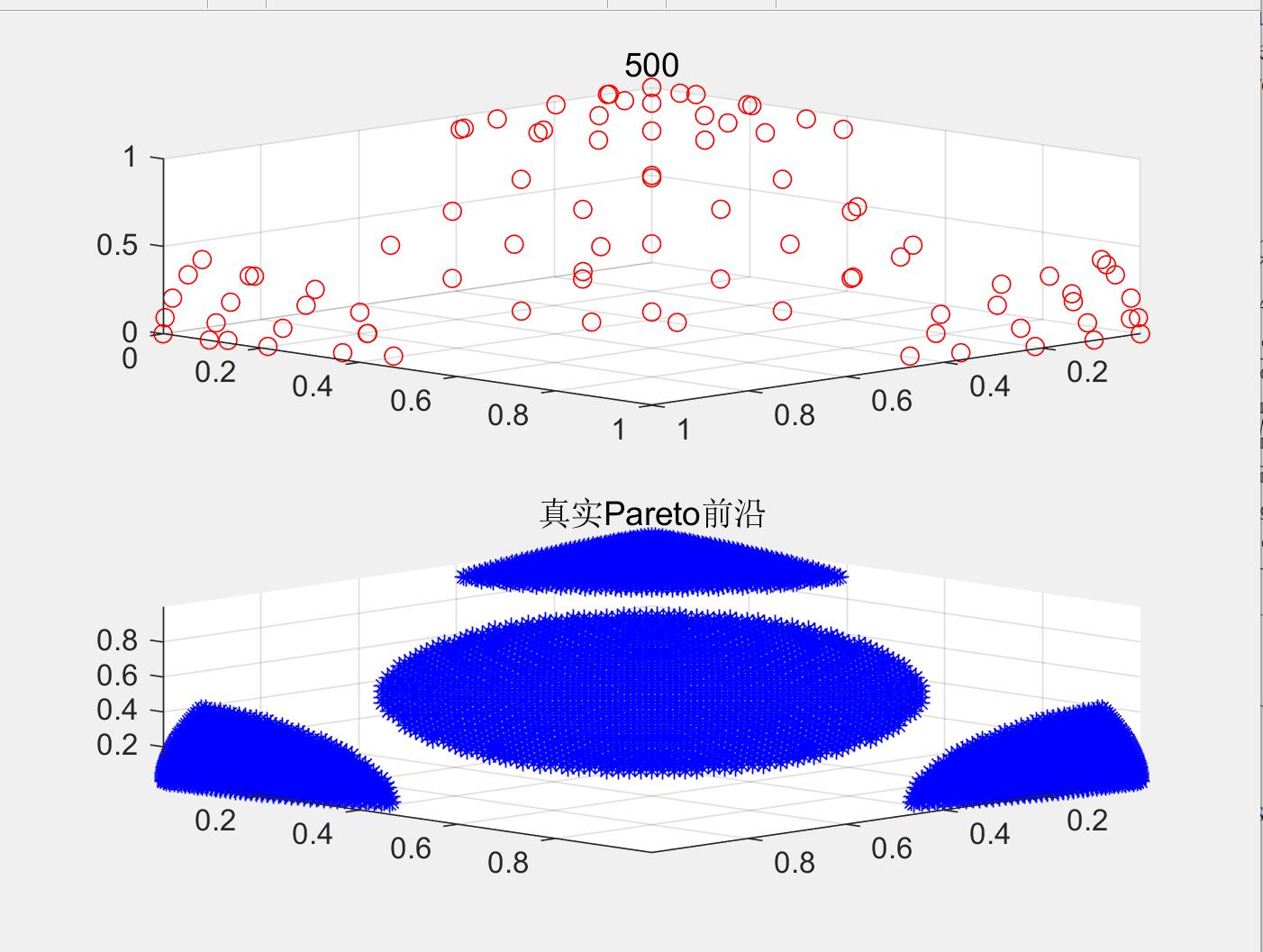
为庆祝此役的胜利，附上C2_DTLZ2 test problem的运行结果：