铁磁共振到底是什么情况？

Posted 2022-12-12 卓晴

 

01 铁磁共振

---

铁磁谐振中到底发生了什么？

一、背景介绍

  今天看到B站上UP主雪域天鹅给出的一段有趣的实验视频，展示了电感电容谐振现象。 猛一看视频似乎仅仅是说明了LC串联谐振现象，但看过之后发现这与普通物理书中简单讨论的LC串联谐振还是有区别的。 通常情况下，电路中元器件的参数一旦确定，在输入的交流信号参数也确定的情况下谐振一定会产生。 但视频中，则需要变压器副边进行短路才能够激发电路的共振，使得电灯泡的输出电压增加。这到底是怎么一回事呢？

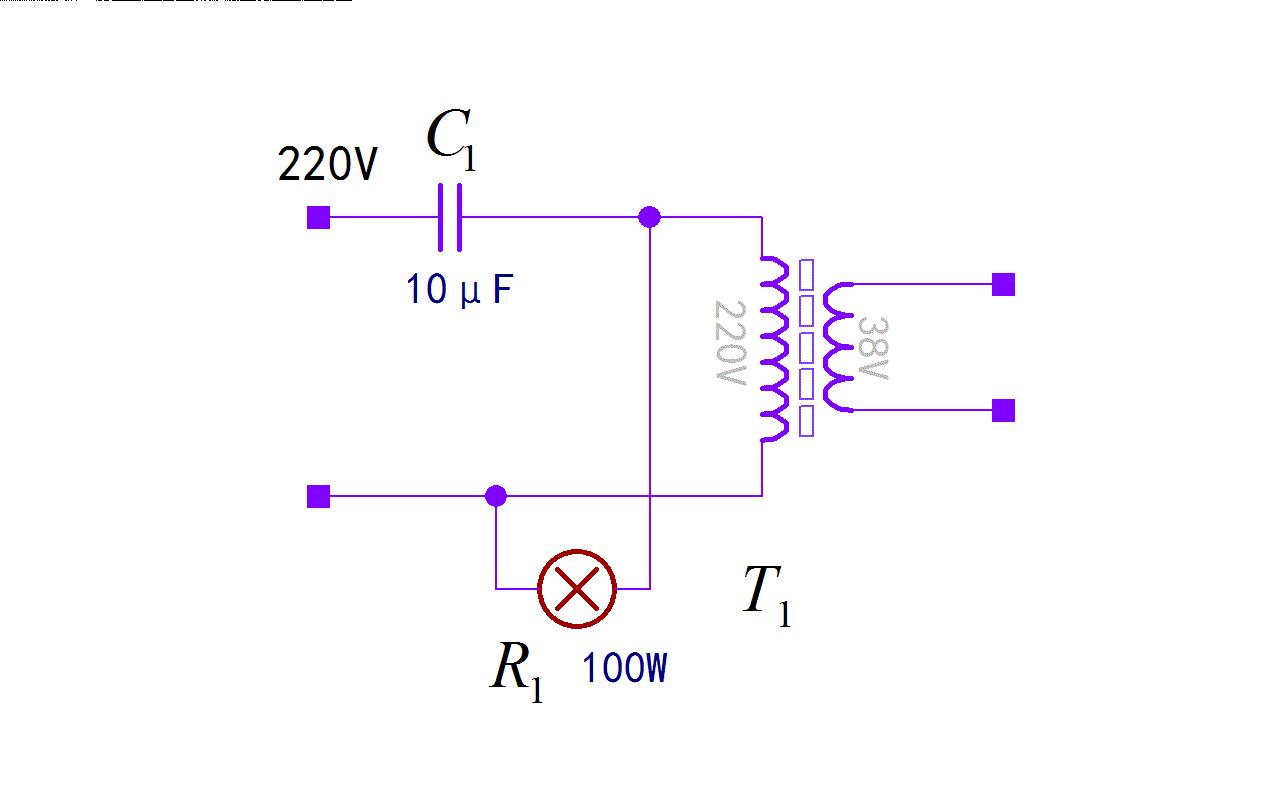
  根据视频中的介绍，可以绘制出实验电路。 使用了一个10微法，400V的洗衣机电机启动电容， 与一个220V输入，38V输出大约0.7A的普通工字型变压器的原边串联。 将一个100W的白炽灯泡并联在变压器的原边。 因此构成了一个RLC串并联谐振回路。 这里的电容C1，电阻R1的参数都知道，但变压器T1的参数不知道。 有趣的是，一开始电路灯泡上的电压为220V。将变压器输出副边短路之后，灯泡上的电压开始急剧上升。 录像中可以看到，灯泡两端的电压U2， 可以达到390V左右的高压。 即使将变压器副边短路去掉，似乎变压器具有记忆能力似的，U2的高压依然维持。 电路也会自行回到最初的状态，灯泡上的电压下降到220V左右。 这究竟是怎么一回事呢？

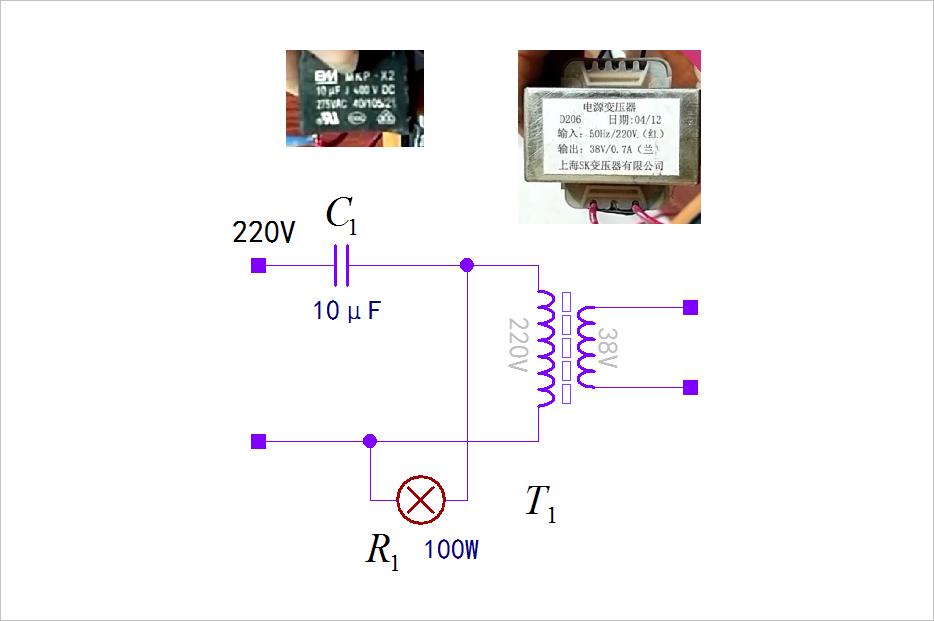
▲ 图1.1.1 视频中实验电路图

二、理论分析

  这里将变压器的原边简化成电感L1， 电灯泡等效成阻值为484欧姆的电阻。 电容参数为10微法， 只有电感的参数不知道，一般小型变压器变压器原边的电感在1亨左右。 根据简化后的电路图， 可以写出电灯泡上的分压U2的大小公式。 这是绘制不同的电感L1的取值，对应的U2的大小。 可以看到当电感L1为1H左右的时候，U2的电压处在谐振状态，可以达到340V左右。 但实验中谐振的电压可以达到390V。这是由于电灯泡的电阻会随着输入电压增加而上升。 这里绘制出灯泡电阻从450欧姆变化到750欧姆， 对应了不同的谐振曲线。可以看到电阻越大，谐振时U2越大， 最大值甚至烧过了500V。

  由于LC谐振使得灯泡两端的电压升高，这个问题我们分析清楚了。 但其中最神秘的是， 为什么电路谐振需要经过变压器副边进行短路激发才能够产生呢？ 似乎电路具有某种记忆的能力， 它能够知道自己被激发了，同时还可以自动恢复到原来没有谐振的状态。

1、实验电路图

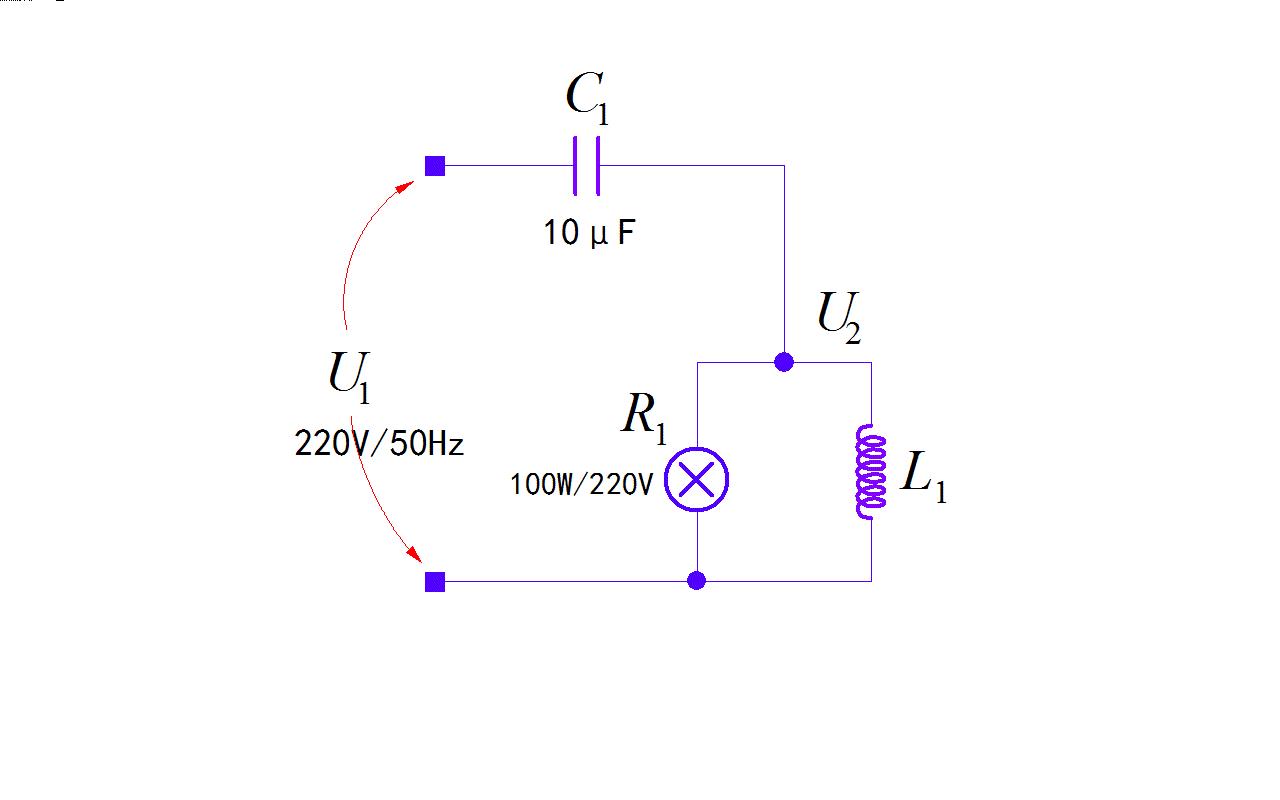
  根据实验中UP主的元器件的连接关系，可以绘制出实验电路图，如下图所示：

▲ 图1.2.1 视频中的实验电路图

2、数学推导

  根据上述实验电路图，将变压器 $T_1$ 等效成一个电感 $L_1$ 。因此上述实验电路可以简化成如下的电路图。

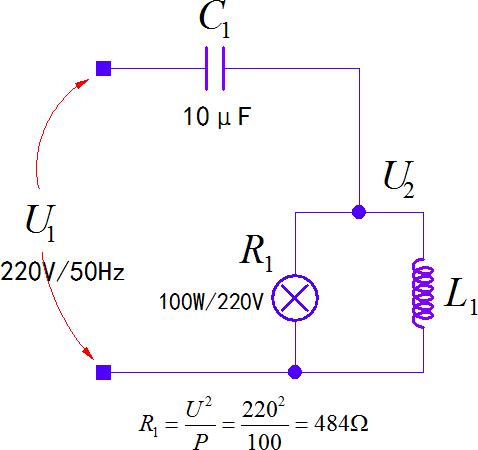
▲ 图1.2.2 简化后的实验电路图

实验电路图参数：

R1：484Ω（随着工作电压是变化的阻值）
C1：10微法
L1：未知
F1：50Hz

  当输入电压为 220V/50Hz的时候，根据电路可以推导出电灯泡上的电压为：

$$U_2=U_1\frac{R_1//j\omega L_1}{\frac{1}{j\omega C_1}+R_1//j\omega L_1}=U_1\frac{-{\omega }^2{R}_1{C}_1{L}_1}{-{\omega }^2{R}_1{C}_1{L}_1+j\omega L_1+R_1}$$

（1）利用Python进行化简

  为了确认上述推导公式是否正确，下面是Python符号推导程序对结果进行化简。

from headm import *
from sympy                  import symbols,simplify,expand,print_latex
from sympy                  import *

r1,l1,c1,f1 = symbols('r1,l1,c1,f1')

rl = 1j*2*pi*f1*r1*l1/(r1+1j*2*pi*f1*l1)
ratio = rl/(rl+1/(1j*2*pi*f1*c1))

result = simplify(ratio)

print_latex(result)
_=tspexecutepythoncmd("msg2latex")
clipboard.copy(str(result))

  下面是给出的分压比：

$$Ratio=\frac{2.0{\pi }^2{c}_1{f}_1^2{l}_1{r}_1}{2.0{\pi }^2{c}_1{f}_1^2{l}_1{r}_1-1.0i\pi f_1{l}_1-0.5r_1}$$

（2）电感对输出电压影响

  下面给出了对于电感 $L_1$ 取不同的值，对应的输出电压 $U_2$ 的幅值。可以看到当电感大约在1H 左右的时候，输出的电压 U2 达到了峰值，大约 334V。

▲ 图1.2.3 不同电感下输出电压U2的幅值

  在实验中，输出的电压似乎比上面的峰值 334V 大，这实际上是由于电灯泡对应的电阻 R1 会随着电压的升高（对应钨丝的温度上升）它的组织也会升高。 下面给出了灯泡电阻从 450欧姆 变化到 750欧姆是，对应的 U2 的谐振曲线。可以看到 R1 阻值越高，U2 的谐振点呀也就越大。

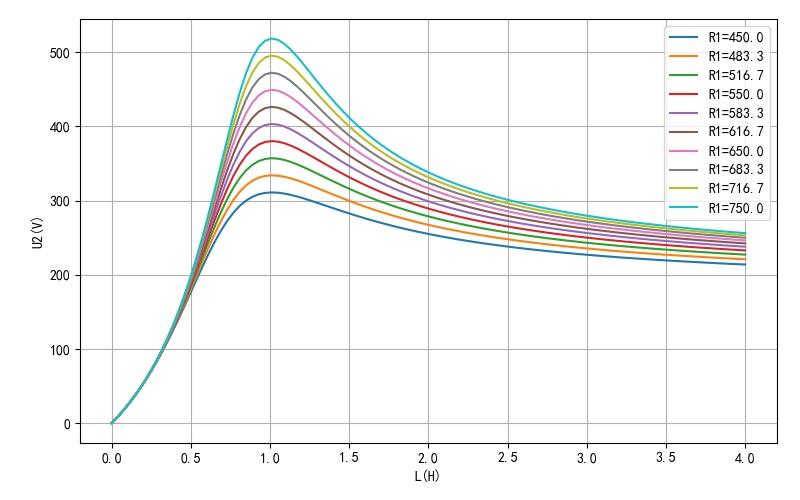
▲ 图1.2.4 不同灯泡电阻下U2的谐振曲线

from headm import *

r1 = 484
c1 = 10e-6
f1 = 50
U1 = 220

ldim = linspace(0, 4, 100)

def U2(l):
    global r1,c1,f1,U1

    omiga = 2*pi*f1
    v = -omiga**2*r1*c1*l
    return U1*abs((v/(v+1j*omiga*l+r1)))

rdim = linspace(450, 750, 10)

for r1 in rdim:
    u2dim = []
    for l in ldim:
        u2dim.append(U2(l))

    plt.plot(ldim, u2dim, label='R1=%4.1f'%r1)

    plt.xlabel("L(H)")
    plt.ylabel("U2(V)")
    plt.grid(True)
    plt.legend(loc='upper right')
    plt.tight_layout()
plt.show()

三、问题分析

 

※ 总  结 ※

---

  本文分析了一段视频中演示的LC谐振现象。 但其中遗留的问题远比我们知道的原理还多。 仅仅利用已知的LC串联谐振的原理还无法解释视频中所有的现象。 你们怎么看呢？

---

● 相关图表链接:

• 图1.1.1 视频中实验电路图
• 图1.2.1 视频中的实验电路图
• 图1.2.2 简化后的实验电路图
• 图1.2.3 不同电感下输出电压U2的幅值
• 图1.2.4 不同灯泡电阻下U2的谐振曲线