无重复全排列

Posted 2022-12-12 yuyaweibest

全排列的递归实现

　　递归就是子程序（或函数）直接调用自己或通过一系列调用语句间接调用自己，是一种描述问题和解决方案的基本方法。递归通常用来解决结构自相似的问题，问题的解决可以分为两部分：第一部分是一些特殊情况，有直接的解法；第二部分与原问题相似，但比原问题的规模小。递归是把一个不能或不好解决的大问题转化为一个或几个小问题，再把这些小问题进一步分解成更小的问题，直到每个小问题都可以直接解决。所以，递归有两个基本要素：
　　（１）边界条件：确定递归到何时终止，也称为递归出口。
　　（２）递归模式：大问题如何分解为小问题，也称为递归体。
　　递归的函数调用原则：所有被调用的函数都将创建一个副本，各自为调用者服务，而不受其他函数的影响。如果把调用递归函数的主函数称为第0层，进入函数后，首次递归调用自身称为第1层调用；从第i层递归调用自身称为第i+1层。反之，退出第i+1层调用应该返回第i层。
　　
　　问题描述：用Ｃ++实现：输入需要全排列的个数n(n>=1)，然后输出１—n的全排列，并同时输出全排列的个数。
　　解决思路与方案：为了方便起见，用123来示例下。123的全排列有123、132、213、231、312、321这六种。我们要对123进行全排列。我们可以采用将“1”固定，“23”进行全排列，将“2”固定，对“13”全排列。将“3”固定，对“12”全排列。这其实就是首部分别为”1“，“2”和“3”，其余的数再进行全排列。用递归的思路实现：第一、二和三位数分别与第一位进行交换，其余的数再进行全排列，但是其余数全排后需要再交换回来，以恢复成原始的第一个排列，第一个排列为参照物，否则若不交换回来，则虽然数量与正确解法相同，但会出现重复排列的现象。
　　无重复的n个数全排类似，第１个数分别与第１、２、３.……n个数进行交换，然后其余的n－１个数用递归全排，全排后再交换回来即可。
　　
　　Ｃ++代码实现：

版本１：

#include <iostream>
using namespace std;
const int Maxsize=100;
int a[Maxsize];
void exchange(int *p,int *q);  //交换指针p,q的指向值
void full_array(int x ,int y); //全排函数
int sum=0;                     //sum用于统计全排的个数 
int main()
int n;
cout<<"全排列1-n的整数，请输入不小于1大于100的整数n: ";
cin>>n;
if(n>Maxsize||n<1)             //如果n不在限定范围，输出错误
    cout<<"Error:请输入设定范围的n! ";
for(int i=0;i<n;++i) 　　　　　　//把数组a[0]—a[n-1]分别赋值1—n
a[i]=i+1;
full_array(0,n);                 
cout<<"全排列数目为： "<<sum;
cin.get();
cin.get();
return 0;

void exchange(int *p,int *q)
    int temp;
    temp=*p;
    *p=*q;
    *q=temp;

void full_array(int x ,int y)
int k=0;
if(x==y-1)                //如果x==y-1说明递归区间只剩下一个数，直接输出

    for(k=0;k<y;k++)
        cout<<a[k]<<' ';
    sum++;
    cout<<endl;

else

for (k=x;k<y;k++)          //第k个数分别与[x,y-1]内的数交换得新排列

    exchange(&a[k],&a[x]);
    full_array(x+1,y);
    exchange(&a[x],&a[k]);

测试：
输入４:
输出：

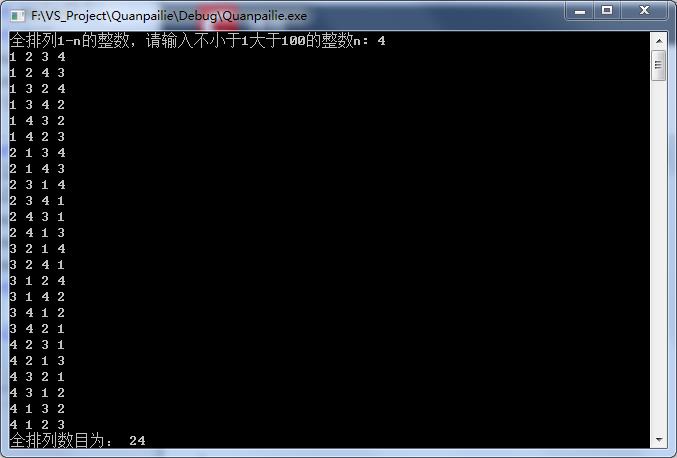
其他测试类似，均能输出正确结果，实验成功！

版本２：

#include <iostream>
using namespace std;
int num[4];
int maxn=4;
int x=1;
void chushi()

    int i;
    for(i=0;i<maxn;i++)
        num[i]=i+1;

void put()

    int i;
    cout<<"第"<<x++<<"组:";
    for(i=0;i<maxn;i++)
        cout<<num[i]<<" ";
    cout<<endl;

void exchange1(int min,int max)//循环右移一位，下标max移动到下标min,1234移动为4123

    int i;
    int temp=num[max];
    for(i=max;i>min;i--)
        num[i]=num[i-1];
    num[min]=temp;

void exchange2(int min,int max)//循环左移一位至数组还原

    int i;
    int temp=num[min];
    for(i=min;i<max;i++)
        num[i]=num[i+1];
    num[max]=temp;

void full_array(int x,int y)

    if(x==y-1)
    
        put();
        return;
    
    int i;
    for(i=x;i<y;i++)
    
        exchange1(x,i);     //下标下限x到上限i循环移动一位，可等效num[x]与num[i]交换
        full_array(x+1,y);　　
        exchange2(x,i);
    

int main()

    chushi();
    full_array(0,maxn);
    cin.get();
    return 0;

输出：

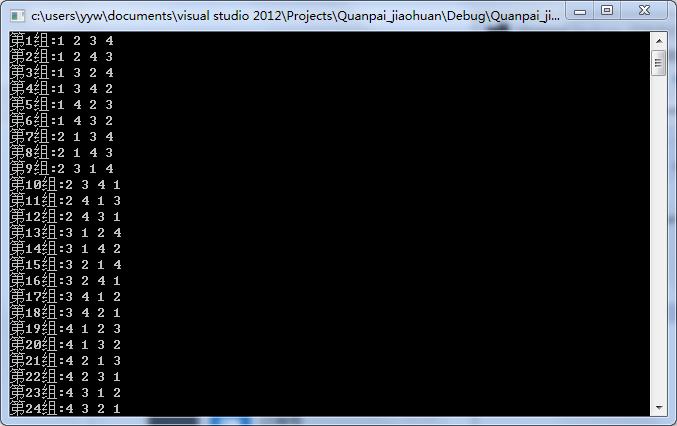
其他测试类似，均能输出正确结果，实验成功！

版本3：

#include <iostream>
#include <vector>             　　   //使用vector容器
using namespace std;
void exchange(vector<int> *vector,int i,int j);  //交换vector容器内元素
void full_array(vector<int> *vector,int x,int y);
int sum=0;
int n;
vector <int>::iterator it;
int main()
vector<int> *vec;　　　　　　　       //声明一个int型向量指针vec　　　　　
vec=new vector<int>();              //用运算符new动态申请内存，此为必须
cout<<"请输入全排列的个数n: ";
cin>>n;
if(n<1)
    cout<<"Error:请输入设定范围的n! ";
for(int i=0;i<n;++i)
    (*vec).push_back(i+1);　　//使用push_back函数在数组的最后添加一个数据
full_array(vec,0,n);
cout<<"全排列数目为： "<<sum;
cin.get();
cin.get();
delete vec;                         //删除分配的内存
return 0;

void exchange(vector<int> *vector,int i,int j)
    int temp;
    temp=(*vector)[i];
    (*vector)[i]=(*vector)[j];
    (*vector)[j]=temp;

void full_array(vector<int> *vector,int x,int y)


    int k=0;
    if(x==y-1)           //使用迭代器it访问vector内成员并输出
    
        for(it=(*vector).begin();it!=(*vector).end();it++)
            cout<<*it<<' ';
        sum++;
        cout<<endl;
    
    else
    
        for(k=x;k<y;k++)
        
            exchange(vector,k,x);
            full_array(vector,x+1,y);
            exchange(vector,k,x);
        
    

测试：
输入４:
输出：

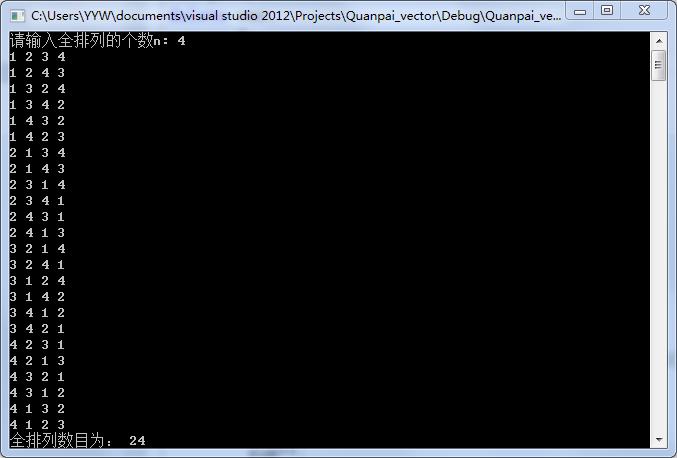
其他测试类似，均能输出正确结果，实验成功！

版本4：

#include <iostream>
#include <vector>
using namespace std;
void exchange(vector<int> &vector,int i,int j);
void full_array(vector<int> &vector,int x,int y);
int sum=0;
int main()
vector<int> vec;
int n;
cout<<"请输入全排列的个数n: ";
cin>>n;
if(n<1)
    cout<<"Error:请输入设定范围的n! ";
for(int i=0;i<n;++i)
    vec.push_back(i+1);
full_array(vec,0,n-1);
cout<<"全排列数目为： "<<sum;
cin.get();
cin.get();
return 0;

void exchange(vector<int> &vector,int i,int j)//&为C++引用，不加&，则值不交换

    int temp;
    temp=vector[i];
    vector[i]=vector[j];
    vector[j]=temp;

void full_array(vector<int> &vector,int x,int y)

    int k=0;
    if(x==y)
    
        for(k=0;k<=y;k++)
            cout<<(vector)[k]<<' ';　//vector可直接通过下脚标直接访问
        sum++;
        cout<<endl;
    
    else
    
        for(k=x;k<=y;k++)
        
            exchange(vector,k,x);
            full_array(vector,x+1,y);
            exchange(vector,k,x);
        
    

测试：
输入４:
输出：

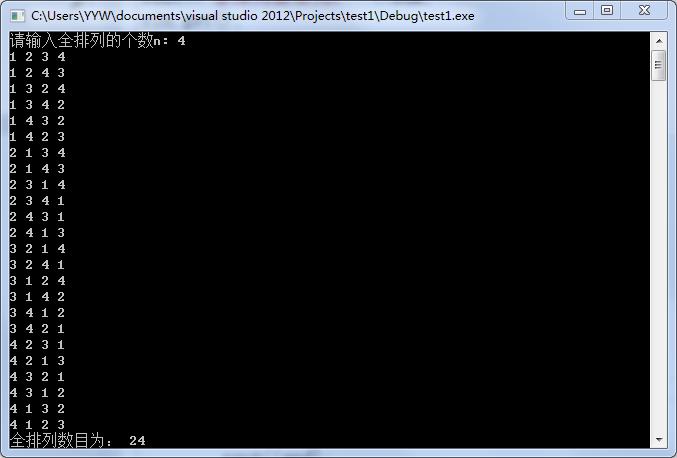
其他测试类似，均能输出正确结果，实验成功！

分析并比较四个版本：
１：版本3和4较1和2，使用了vector向量，它是C++中的一种数据结构，确切地说是一个类，它相当于一个动态的数组，当程序员无法知道自己需要的数组的规模多大时，用其来解决问题可以达到最大节约空间的目的。vector 容器与数组相比，其优点在于它能够根据需要随时自动调整自身的大小以便容下所要放入的元素。此外, vector 也提供了许多的方法来对自身进行操作，详见vector的用法详解。
２：这四种方法均是用了递归的思想解决无重复全排列问题，大同小异，纯粹是为了供作者以后复习使用，所以才全部展现出来。第1、3和4版本思想完全一样：第１个数分别与第１、２、３.……n个数进行交换，然后其余的n－１个数用递归全排，全排后再交换回来即可。第2个版本稍有不同，分别利用数组的整体循环右移一位来达到交换目的，递归，最终再循环左移还原。