堆结构和堆排序的Java实现

Posted 2022-12-12 想作会飞的鱼

一、什么是堆

堆是一棵顺序存储的完全二叉树。关于完全二叉树的定义，其实十分简单。我们都知道满二叉树，也就是所有非叶子结点的节点必有左右两个子节点的树。对于一个完全二叉树而言，如果按照从上到下、从左到右的顺序遍历这棵树，如果遍历的顺序和其对应的满二叉树（把非满的节点用一个预设值填满）完全一致的话，那么这棵树就是完全二叉树。一个通俗的描述就是：一棵树除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐。如下：

上图是一个满二叉树

上图是一个完全二叉树

上图不是一个完全二叉树。（最后一层并未左对齐）

如果一个完全二叉树满足如下条件之一：

• 每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。
• 每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。

举例来说，对于n个元素的序列R[0], R[1], … , R[n]当且仅当满足下列关系之一时，称之为堆：

• R[i] <= R[2i+1] 且 R[i] <= R[2i+2] (小根堆)
• R[i] >= R[2i+1] 且 R[i] >= R[2i+2] (大根堆)
  其中i=1,2,…,n/2向下取整;

如上图所示，序列R10, 8, 9, 7, 3，6，4，1，5，2是一个典型的大根堆。
对于大根堆，设当前元素在数组中以R[i]表示，那么就有，

• 它的左孩子结点是：R[2*i+1];
• 它的右孩子结点是：R[2*i+2];
• 它的父结点是：R[(i-1)/2];
• R[i] >= R[2*i+1] 且 R[i] >= R[2i+2]。

二、如何构建堆（以大根堆为例）

先通过详细的实例图来看一下，如何构建初始堆。设有一个无序序列 1, 3, 4, 5, 2, 6, 9, 7, 8, 10 。那么这个无序序列对应的完全二叉树如下：

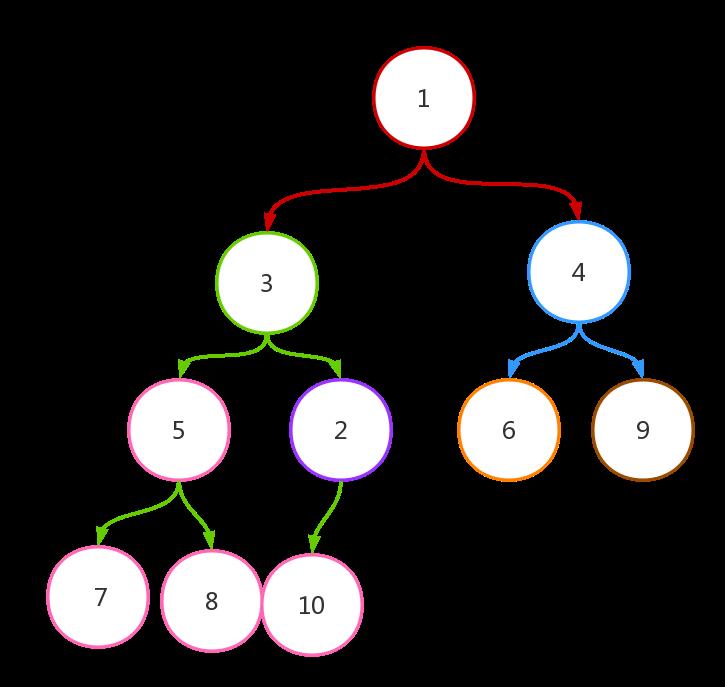
构建这个堆的程序如下：

        // 循环建立初始堆
        //数组已经按照下标顺序（下标从0开始）建立了完全二叉树，我们的目的是调整其为堆
        for (int i = list.length / 2; i >= 0; i--) 
            HeapAdjust(list, i, list.length);
        
        public void HeapAdjust(int[] array, int parent, int length) 
        int temp = array[parent]; // temp保存当前父节点
        int child = 2 * parent + 1; // 先获得左孩子

        while (child < length) //这里length是数组的长度child的值最大等于length-1
            // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
            if (child + 1 < length && array[child] < array[child + 1]) 
                child++;
            

            // 如果父结点的值已经大于孩子结点的值，则直接结束
            if (temp >= array[child])
                break;

            // 把孩子结点的值赋给父结点
            array[parent] = array[child];

            // 选取孩子结点的左孩子结点,继续向下筛选
            parent = child;//更新当前父节点
            child = 2 * child + 1;//更新父节点的左孩子
        

        array[parent] = temp;//把最初的父节点值放到对应的位置
    

• 1、我们首先找到下标为5的节点值，这个节点值为6，经过判断，这个节点没有左节点，所以不执行while循环，直接进行下一步。
  继续找到下标为4的节点值，这个节点值为2，它有左节点，进行while循环。找到子节点中较大的那个与父节点值比较，如果比父节点大则交换两者的值，否则直接退出。其交换结果如下：
  

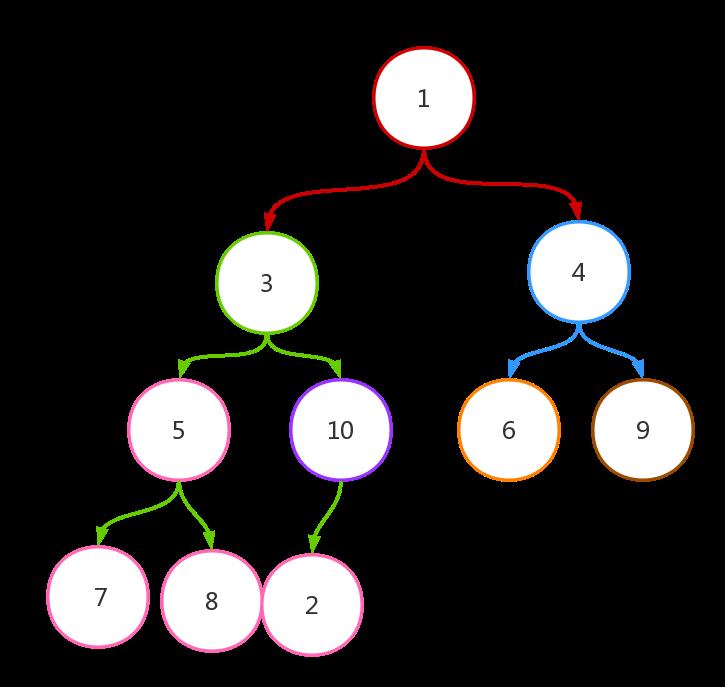
• 2、继续找下标为3的节点，其对应节点值为5。其子节点值为7和8，其交换后的结果如下：
  

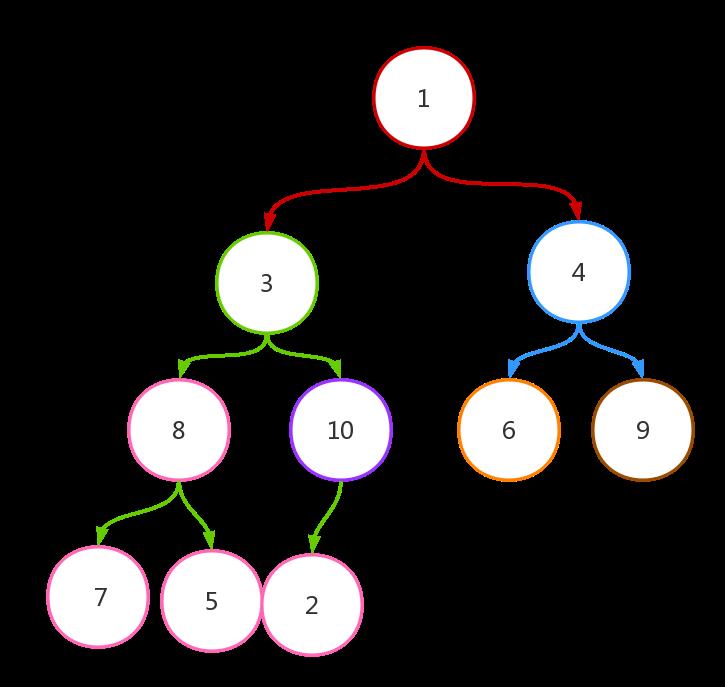
• 3、继续找下标为2的节点，其对应节点值为4。其子节点值为6和9，其交换后的结果如下：
  

• 4、继续找下标为1的节点，其对应节点值为3。其子节点值为8和10，其交换后的结果如下：
  

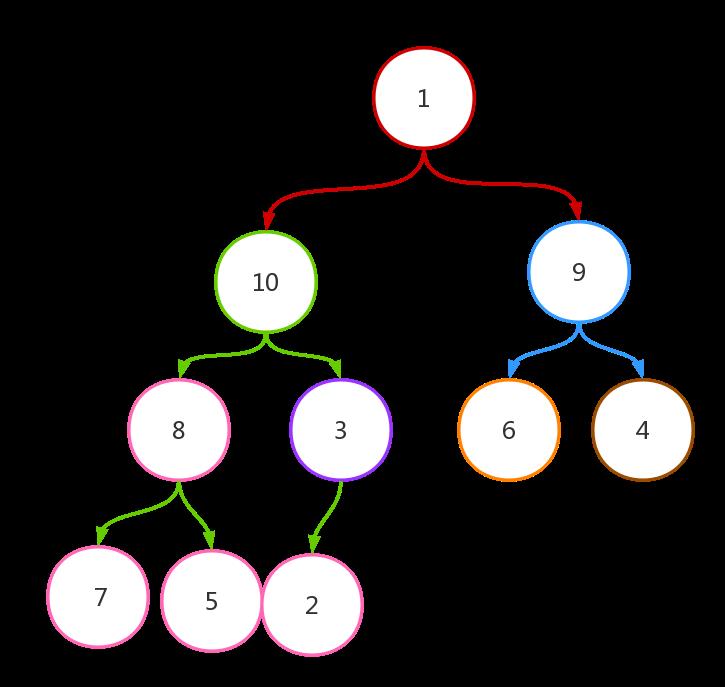
• 5、继续找下标为0的节点，其对应节点值为1。其子节点值为10和9，此时while循环会进行多次，直到1放到了对应的位置。第一次while循环后的结果如下：
  
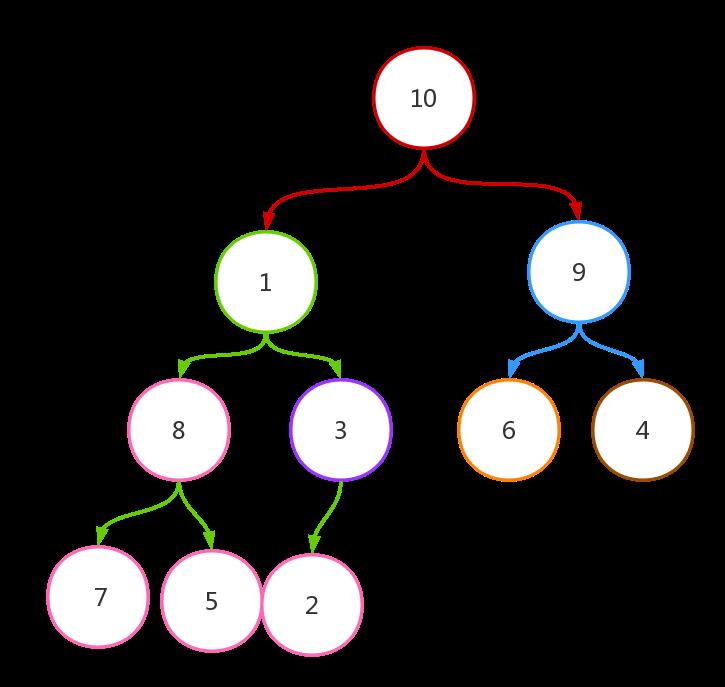
  第二次while循环后的结果如下：
  
  第三次while循环后的结果如下：
  

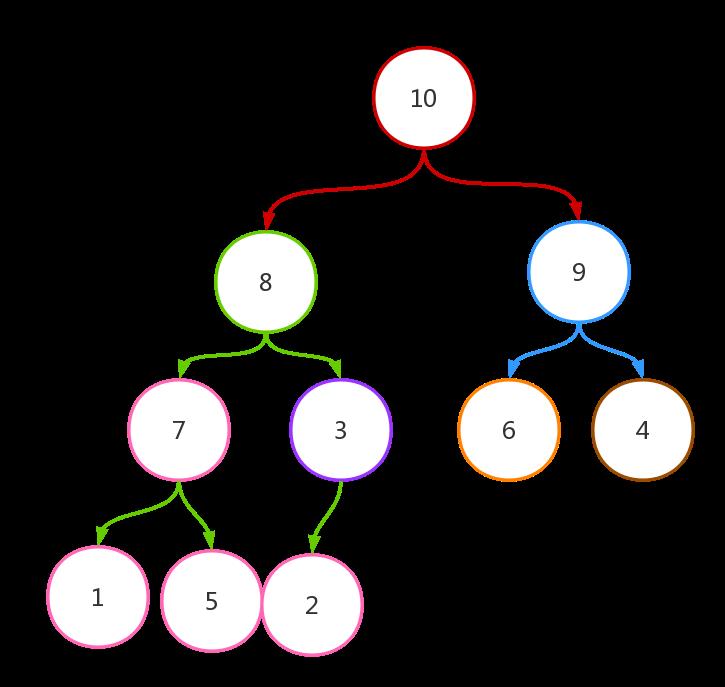
至此，我们构建最大堆的任务便完成了。

三、堆排序

实现堆排序的步骤（基于大根堆）：

• 将存放在array[0，…，n-1]中的n个元素建成初始堆；
• 将堆顶元素与堆底元素进行交换，则序列的最大值即已放到正确的位置；
• 但此时堆被破坏，将堆顶元素向下调整使其继续保持大根堆的性质，再重复第②③步，直到堆中仅剩下一个元素为止。

代码如下：

public class HeapSort 

    public void HeapAdjust(int[] array, int parent, int length) 
        int temp = array[parent]; // temp保存当前父节点
        int child = 2 * parent + 1; // 先获得左孩子

        while (child < length) //这里length是数组的长度child的值最大等于length-1
            // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
            if (child + 1 < length && array[child] < array[child + 1]) 
                child++;
            

            // 如果父结点的值已经大于孩子结点的值，则直接结束
            if (temp >= array[child])
                break;

            // 把孩子结点的值赋给父结点
            array[parent] = array[child];

            // 选取孩子结点的左孩子结点,继续向下筛选
            parent = child;//更新当前父节点
            child = 2 * child + 1;//更新父节点的左孩子
        

        array[parent] = temp;//把最初的父节点值放到对应的位置
    

    public void heapSort(int[] list) 
        // 循环建立初始堆
        //数组已经按照下标顺序（下标从0开始）建立了完全二叉树，我们的目的是调整其为堆
        for (int i = list.length / 2; i >= 0; i--) 
            HeapAdjust(list, i, list.length);
        

        // 进行n-1次循环，完成排序
        for (int i = list.length - 1; i > 0; i--) 
            // 最后一个元素和第一元素进行交换
            int temp = list[i];
            list[i] = list[0];
            list[0] = temp;

            // R[0] 结点破环的原来堆的结构，需要重新调整其顺序，得到i（下标从0到i-1）个结点的堆
            //第一次循环式执行的就是调整length-1个节点形成堆（下标从0到length-2,排除了最大的一个数）
            HeapAdjust(list, 0, i);
            System.out.format("第 %d 趟: \\t", list.length - i);
            printPart(list, 0, list.length - 1);
        
    

    // 打印序列
    public void printPart(int[] list, int begin, int end) 
        for (int i = 0; i < begin; i++) 
            System.out.print("\\t");
        
        for (int i = begin; i <= end; i++) 
            System.out.print(list[i] + "\\t");
        
        System.out.println();
    

    public static void main(String[] args) 
        // 初始化一个序列
        int[] array =  1, 3, 4, 5, 2, 6, 9, 7, 8, 10 ;

        // 调用快速排序方法
        HeapSort heap = new HeapSort();
        System.out.print("排序前:\\t");
        heap.printPart(array, 0, array.length - 1);
        heap.heapSort(array);
        System.out.print("排序后:\\t");
        heap.printPart(array, 0, array.length - 1);
    

其运行结果如下：

排序前:    1   3   4   5   2   6   9   7   8   10  
第 1 趟:  9   8   6   7   3   2   4   1   5   10  
第 2 趟:  8   7   6   5   3   2   4   1   9   10  
第 3 趟:  7   5   6   1   3   2   4   8   9   10  
第 4 趟:  6   5   4   1   3   2   7   8   9   10  
第 5 趟:  5   3   4   1   2   6   7   8   9   10  
第 6 趟:  4   3   2   1   5   6   7   8   9   10  
第 7 趟:  3   1   2   4   5   6   7   8   9   10  
第 8 趟:  2   1   3   4   5   6   7   8   9   10  
第 9 趟:  1   2   3   4   5   6   7   8   9   10  
排序后:    1   2   3   4   5   6   7   8   9   10  

时间复杂度

堆所对应的二叉树为完全二叉树，而完全二叉树通常采用顺序存储方式。当想得到一个序列中第k个最小的元素之前的部分排序序列，最好采用堆排序。因为堆排序的时间复杂度是O(n+klog2n)，若k≤n/log2n，则可得到的时间复杂度为O(n)。

算法稳定性

堆排序是一种不稳定的排序方法。因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径，其查找的顺序和数组中排列的顺序是不同。因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。如下面这种情况：[1,2,2]进行堆排序的时候，两个2的次序便发生了交换。