力扣刷题：二叉搜索树中第K小的元素（java实现）

Posted 2022-12-12 谦谦均

题目：给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

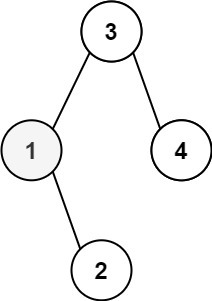
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

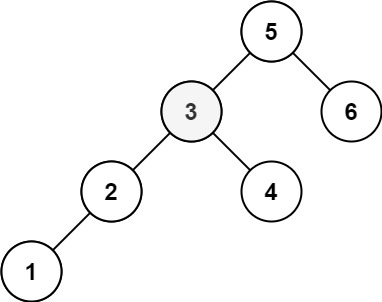
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

• 树中的节点数为 n 。
• 1 <= k <= n <= 10^4
• 0 <= Node.val <= 10^4

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

相关标签：树、深度优先搜索、二叉搜索树、二叉树

解析：
搜索二叉树介绍：二叉查找树（英语：Binary Search Tree），也称为有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树；

二叉搜索树有一个非常重要的特性：二叉搜索树的中序遍历结果一定是有序的。
按照这个特性，可以使用二叉树的中序遍历算法来实现。
方法一：迭代法（二叉树的中序遍历）

public int kthSmallest(TreeNode root, int k) 
        //定义一个栈来维护遍历过的结点，先入后出
        Stack<TreeNode> stack = new Stack<>();
        //标记结点的索引，初始是1。（因为第k个是从1开始数的）
        int sign = 1;
        while (!stack.isEmpty()||root!=null)
            if(root!=null)
                //如果当前结点不是空，就入栈，知道找到最左的结点
                stack.push(root);
                root = root.left;
            else 
                //当前结点是空，说明上一个结点就是最左结点
                root = stack.pop();
                if(k == sign )
                    //当前结点就是答案
                    return root.val;
                else 
                    sign++;
                
                //说明当前root结点以及左子数的都不是第k小的
                //这时遍历右子树
                root = root.right;
            
        
        return 0;
    

方法二：递归法。
大概思路：因为搜索二叉树的中序遍历一定是排序的，而且是从小到大。如果左子树的结点个数比k大，说明要找的结点在左边。如果左子树的结点个数+1等于k，说明根节点就是要找的结点，同理如果k大于左边结点个数+1，就在右边。
具体代码如下所示：

public int kthSmallest(TreeNode root, int k) 
        //获取左子树的结点数量
        int left = getNodeNumber(root.left);
        //如果左子树结点数量大于k，说明要找的就在左边
        if(left>=k)
            //如果左子树的结点个数大于k，说明第k小在左子树
            return kthSmallest(root.left,k);
        else if(left+1==k)
            //如果左子树结点个数+1等于k，说明根节点就是要找的结点
            return root.val;
        else 
            //如果左子树结点个数+1小于k，说明要找的结点在右子树
            return kthSmallest(root.right,k-left-1);
        
    
    //获取二叉树结点个数的方法
    public int getNodeNumber(TreeNode treeNode)
        if(treeNode==null)
            return 0;
        
        return 1+getNodeNumber(treeNode.left)+getNodeNumber(treeNode.right);
    

看到这里
别卷了，休息会儿吧~