图像基本知识整理——图像的正交变换
Posted Lyndon_zheng
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图像基本知识整理——图像的正交变换相关的知识，希望对你有一定的参考价值。
变换是将一个域的特征变换到另一个域，可能使在一个域不突出的特征在另一个域突出。这有助于对有用信号的提取与应用。 一、傅里叶变换 傅里叶变换是一种将时域信号转换到频域的方式，其在图像处理和分析方面有很多优势。 对于一幅图像， 图像中灰度变化缓慢的区域对应于较低的频率，而灰度变化较快的区域对应高频信息。因此，在频域图像中能量主要集中在低频部分，只有小部分的能量在高频部分。这一点在直观上也比较好理解，频率反映的是 信号变化的快慢，变化快的频率高，变化慢的频率低，在图像中边缘的信号变化明显，这样才能与周围对比度增强，因此边缘的多对于高频。 1、基本原理 图像的傅里叶变换与一般信号的变化类似。而在实际应用中，傅里叶变换的计算量很大，在处理图像时效率很低，所以引入了快速傅里叶变化。 2、代码实现void fft2D(unsigned char* imgBuf, int width, int height)
int i, j, u, v;
float *buf = new float[width*height * 2];
for (i = 0; i<width*height; i++)
buf[i * 2 + 0] = imgBuf[i];
buf[i * 2 + 1] = 0;
float *array = new float[height * 2];
for (u = 0; u<width; u++)
for (v = 0; v<height; v++)
array[v * 2 + 0] = buf[v*width * 2 + u * 2 + 0];
array[v * 2 + 1] = buf[v*width * 2 + u * 2 + 1];
fft1D(array, width);
for (v = 0; v<height; v++)
buf[v*width * 2 + u * 2 + 0] = array[v * 2 + 0];
buf[v*width * 2 + u * 2 + 1] = array[v * 2 + 1];
delete[]array;
for (v = 0; v<height; v++)
fft1D(buf + v*width * 2, width);
//频域数据保存至fftBuf
fftBuf = buf;
//修改频域数据
int off;
//显示需要
float *buf1 = new float[width*height];
for (i = 0; i<width*height; i++)
buf1[i] = sqrt(buf[i * 2 + 0] * buf[i * 2 + 0] + buf[i * 2 + 1] * buf[i * 2 + 1]);
int mo = 2000;//模值
for (i = 0; i<width*height; i++)
if (buf1[i] / mo>255)
imgBuf[i] = 255;
else imgBuf[i] = buf1[i] / mo;
delete[]buf1;
二、K-L变换 K-L变换也叫做特征矢量、主分量变换。我们都知道在数理统计中，可以将多个相关的因素通过一组相互独立的变量来重新表示。 1、基本原理 首先看一个简单例子：假设x=(x1,x2)的四次观测点分别为(2,2) (1,1)(-1,-1)(-2,-2),求其K-L变换。
将二维数据变换到一维直线上，数据量变小了。
同理，
对于单幅图像，我们可以求出其主分量，然后通过对主分量的旋转实现图像的旋转，也可用于单幅图像的
降维处理。
K-L变换是基于统计特性基础的一种个变换，也可用于图像信号传输编码和多通道多幅图像的主信号分析中。
K-L变换虽然具有MSE意义下的最佳性能，但需要先知道信源的协方差矩阵并求出特征值。求特征值与特征向量并不是一件容易的事，维数较高时甚至求不出来。即使能借助计算机求解，也很难满足实时处理的要求，而且从编码应用看还需要将这些信息传输给接收端。这些因素造成了K-L变换在工程实践中不能广泛使用。人们一方面继续寻求解特征值与特征向量的快速算法，另一方面则寻找一些虽不是“最佳”、但也有较好的去相关与能量集中的性能且容易实现的一些变换方法。而K-L变换就常常作为对这些变换性能的评价标准。
在图像选择中，涉及比较多的子函数，就不在此上传。
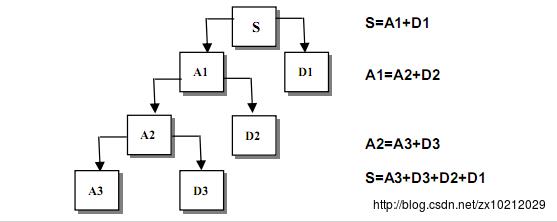
三、小波变换 在信号处理中，我们知道 傅里叶变换是一种全局变换，要么完全在时间域，要么完全在频率域，它是以两个方向上都无限伸展的正弦信号波作为正交基函数，因此无法表述信号的时频局部性质。为了分析和处理非平稳信号，能够对瞬态信息和局部信息（边缘）进行分析，可以在傅里叶分析的理论基础上，定义有限宽度的基函数来表示信号，这种有限宽度的波就叫做小波。 小波变换克服了傅里叶变换的不足，目前在信号处理、模式识别、语音识别等很多方面都有了不错的发展。小波变换的思想，能够广泛用于各种信号数据的处理。(小波变化非常强大，不管是语音信号处理，图像处理还是模式识别等方面都有单独的书籍来进行论述，极其强大的工具) 1、基本原理 小波分析是通过缩放母小波的宽度来获得信号的频率特征，通过平移母小波来获得信号的时间信息。具体原理不再赘述，我的理解 小波变换就是将傅里叶变换的正弦波和余弦波基函数变为有限的小波基函数，然后通过不同的缩放来逼近原始的信号，其系数与傅里叶变换的频率类似，在缩放过程中，我们用越窄的信号去表现高频信息会越完美，所以频率越高，缩放因子越小；而低频信号比较平稳，没有丰富的细节，可用宽的小波信号逼近，所以频率越低，缩放因子越大。 在计算机中，我们通常采用双尺度离散小波变换，也就是将缩放因子和平移参数每次都旋转2的倍数。 如下图所示，其中原信号S通过低频滤波器得到A1，通过高频滤波器得到D1，其中A1表示信号的近似值，也就是大缩放因子产生的系数，D1表示信号的细节值，也就是小缩放因子产生的系数。而且可以对近似值A1进行进一步的小波分析，形成多级小波分析图。
在图像处理中，二维离散小波变换与一维小波变换类似，也是将二维信号在不同尺度上进行分解，得到原始图的近似值和细节值。如图所示的三维小波分解示意图，
LL表示低频分量，也是信号主要的部分；LH表示水平细节分量，为高频成分；HL表示垂直细节分量，高频分量；HH为对角细节分量，也是高频分量。
2、代码实现
//小波基
const double hCoef[10][20] =
.707106781187, .707106781187,
.482962913145, .836516303738, .224143868042, -.129409522551 ,
.332670552950, .806891509311, .459877502118, -.135011020010, -.085441273882, .035226291882 ,
.230377813309, .714846570553, .630880767930, -.027983769417,-.187034811719, .030841381836, .032883011667, -.010597401785 ,
.160102397974, .603829269797, .724308528438, .138428145901, -.242294887066,-.032244869585, .077571493840, -.006241490213, -.012580751999, .003335725285 ,
.111540743350, .494623890398, .751133908021, .315250351709, -.226264693965,
-.129766867567, .097501605587, .027522865530, -.031582039318, .000553842201,
.004777257511, -.001077301085 ,
.077852054085, .396539319482, .729132090846, .469782287405, -.143906003929,
-.224036184994, .071309219267, .080612609151, -.038029936935, -.016574541631,
.012550998556, .000429577973, -.001801640704, .000353713800 ,
.054415842243, .312871590914, .675630736297, .585354683654, -.015829105256,
-.284015542962, .000472484574, .128747426620, -.017369301002, -.044088253931,
.013981027917, .008746094047, -.004870352993, -.000391740373, .000675449406,
-.000117476784 ,
.038077947364, .243834674613, .604823123690, .657288078051, .133197385825,
-.293273783279, -.096840783223, .148540749338, .030725681479, -.067632829061,
.000250947115, .022361662124, -.004723204758, -.004281503682, .001847646883,
.000230385764, -.000251963189, .000039347320 ,
.026670057901, .188176800078, .527201188932, .688459039454, .281172343661,
-.249846424327, -.195946274377, .127369340336, .093057364604, -.071394147166,
-.029457536822, .033212674059, .003606553567, -.010733175483, .001395351747,
.001992405295, -.000685856695, -.000116466855, .000093588670, -.000013264203
;
//一维小波变换
BOOL DWTStep_1D(double* pDbSrc, int nCurLevel,int nInv, int nStep,int nSupp)
double s = sqrt((double)2);
// 获得小波基的指针
double* h = (double*)hCoef[nSupp-1];
// 确认当前层数有效
ASSERT(nCurLevel>=0);
// 计算当前层数的长度
int CurN = 1<<nCurLevel;
if (nInv) CurN <<= 1;
// 确认所选择的小波基和当前层数的长度有效
if (nSupp<1 || nSupp>10 || CurN<2*nSupp)
return FALSE;
// 分配临时内存用于存放结果
double *ptemp = new double[CurN];
if (!ptemp) return FALSE;
double s1, s2;
int Index1, Index2;
// 判断是进行DWT还是IDWT
if (!nInv)
// DWT
Index1=0;
Index2=2*nSupp-1;
// 进行卷积，其中s1为低频部分，s2为高频部分的结果
for (int i=0; i<CurN/2; i++)
s1 = s2 = 0;
double t = -1;
for (int j=0; j<2*nSupp; j++, t=-t)
s1 += h[j]*pDbSrc[(Index1 & CurN-1) * nStep];
s2 += t*h[j]*pDbSrc[(Index2 & CurN-1) * nStep];
Index1++;
Index2--;
// 将结果存放在临时内存中
ptemp[i] = s1/s;
ptemp[i+CurN/2] = s2/s;
Index1 -= 2*nSupp;
Index2 += 2*nSupp;
Index1 += 2;
Index2 += 2;
// 否则进行IDWT
else
// IDWT
Index1 = CurN/2;
Index2 = CurN/2-nSupp+1;
// 进行卷积，其中其中s1为低频部分，s2为高频部分的结果
for (int i=0; i<CurN/2; i++)
s1 = s2 = 0;
int Index3 = 0;
for (int j=0; j<nSupp; j++)
s1 += h[Index3]*pDbSrc[(Index1 & CurN/2-1) * nStep]
+h[Index3+1]*pDbSrc[((Index2 & CurN/2-1) + CurN/2) * nStep];
s2 += h[Index3+1]*pDbSrc[(Index1 & CurN/2-1) * nStep]
-h[Index3]*pDbSrc[((Index2 & CurN/2-1) + CurN/2) * nStep];
Index3+=2;
Index1--, Index2++;
// 将结果存入临时内存
ptemp[2*i] = s1*s;
ptemp[2*i+1] = s2*s;
Index1 += nSupp;
Index2 -= nSupp;
Index1++;
Index2++;
// 将结果存入源图像中
for (int i=0; i<CurN; i++)
pDbSrc[i*nStep] = ptemp[i];
// 释放临时内存，并返回
delete[] ptemp;
return TRUE;
//二维小波变换
BOOL DWTStep_2D(double* pDbSrc, int nCurWLevel, int nCurHLevel,
int nMaxWLevel, int nMaxHLevel, int nInv, int nStep, int nSupp)
// 计算图像的长度和宽度（2次幂对齐）
int W = 1<<nMaxWLevel, H = 1<<nMaxHLevel;
// 计算当前分解的图像的长度和宽度
int CurW = 1<<nCurWLevel, CurH = 1<<nCurHLevel;
// 判断是进行DWT还是IDWT
if (!nInv)
int i = 0;
// 对行进行一维DWT
for (i=0; i<CurH; i++)
if (!DWTStep_1D(pDbSrc+(int)i*W*nStep, nCurWLevel, nInv, nStep, nSupp)) return FALSE;
// 对列进行一维DWT
for (i=0; i<CurW; i++)
if (!DWTStep_1D(pDbSrc+i*nStep, nCurHLevel, nInv, W*nStep, nSupp)) return FALSE;
// 否则进行IDWT
else
// 计算当前变换的图像的长度和宽度
CurW <<= 1;
CurH <<= 1;
int i = 0;
// 对列进行IDWT
for (i=0; i<CurW; i++)
if (!DWTStep_1D(pDbSrc+i*nStep, nCurHLevel, nInv, W*nStep, nSupp)) return FALSE;
// 对行进行IDWT
for (i=0; i<CurH; i++)
if (!DWTStep_1D(pDbSrc+(int)i*W*nStep, nCurWLevel, nInv, nStep, nSupp)) return FALSE;
// 返回
return TRUE;
//数据转换
BYTE FloatToByte(double f)
if (f<=0) return (BYTE)0;
else if (f>=255) return (BYTE)255;
else return (BYTE)(f+0.5);
//数据转换
char FloatToChar(double f)
if (f>=0)
if (f>=127.0)
return (char)127;
else return (char)(f+0.5);
else
if (f<=-128)
return (char)-128;
else return -(char)(-f+0.5);
//数据转换
int Log2(int n)
int rsl = 0;
while (n >>= 1) rsl++;
return rsl;
//图像小波变换
BOOL DIBDWTStep(LPSTR lpDIBBits,double*m_pDbImage, int nWidth,int nHeight, int nInv,int m_nDWTCurDepth,int m_nSupp)
// 循环变量
int i, j;
// 获取变换的最大层数
int nMaxWLevel = Log2(nWidth);
int nMaxHLevel = Log2(nHeight);
int nMaxLevel;
if (nWidth == 1<<nMaxWLevel && nHeight == 1<<nMaxHLevel)
nMaxLevel = min(nMaxWLevel, nMaxHLevel);
// 临时变量
double *pDbTemp;
BYTE *pBits;
// 如果小波变换的存储内存还没有分配，则分配此内存
if(!m_pDbImage)
m_pDbImage = new double[nWidth*nHeight];
if (!m_pDbImage) return FALSE;
// 将图像数据放入m_pDbImage中
for (j=0; j<nHeight; j++)
pDbTemp = m_pDbImage + j*nWidth;
pBits = (unsigned char *)lpDIBBits + (nHeight-1-j)*nWidth;
for (i=0; i<nWidth; i++)
pDbTemp[i] = pBits[i];
// 进行小波变换（或反变换）
if (!DWTStep_2D(m_pDbImage, nMaxWLevel-m_nDWTCurDepth, nMaxHLevel-m_nDWTCurDepth,
nMaxWLevel, nMaxHLevel, nInv, 1, m_nSupp))
return FALSE;
// 如果是反变换，则当前层数减1
if (nInv)
m_nDWTCurDepth --;
// 否则加1
else
m_nDWTCurDepth ++;
// 然后，将数据拷贝回原CDib中，并进行相应的数据转换
int lfw = nWidth>>m_nDWTCurDepth, lfh = nHeight>>m_nDWTCurDepth;
for (j=0; j<nHeight; j++)
pDbTemp = m_pDbImage + j*nWidth;
pBits = (unsigned char *)lpDIBBits + (nHeight-1-j)*nWidth;
for (i=0; i<nWidth; i++)
if (j<lfh && i<lfw)
pBits[i] = FloatToByte(pDbTemp[i]);
else
pBits[i] = BYTE(FloatToChar(pDbTemp[i]) ^ 0x80);
// 返回
return TRUE;
3、算法应用 (1)、边缘检测 在多尺度小波变换后，将最低尺度的近似分量赋值为零，则图像的主要信息丢失，而高频信息都还保留。这时对小波分解的图进行小波反变换，就能够得到原始图像的边缘信息。 (2)、噪声去除 与边缘检测相反，在噪声去除处理中，需要将高频信息去掉。所以可以选择一个阈值，处理高频细节的小波系数，去掉图像中的部分高频信息，从而达到滤波的效果。 (3)、信息编码 小波变换后的LL分量包含了图像的主要信息，可以对该部分进行编码，得到更高的编码效率，而图像基本上不会有失真。 小波变换在图像的很多处理中都有很大的应用，具体的分析将在后续整理中进行详细的描述。
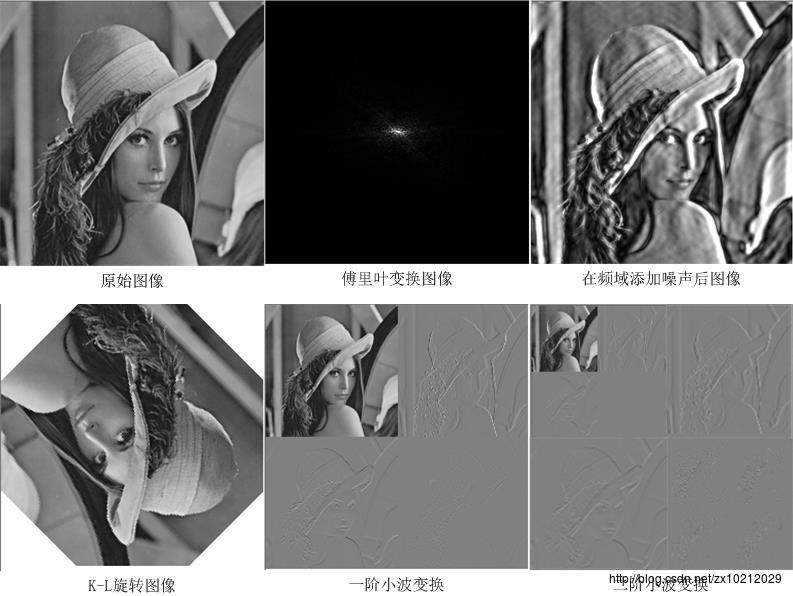
正交变换效果图：
以上是关于图像基本知识整理——图像的正交变换的主要内容，如果未能解决你的问题，请参考以下文章