第十四周 项目3--判断是否为二叉排序树

Posted 2022-12-11 zxt17853535692

问题及代码：

/*
*烟台大学计算机与控制工程学院      
*作    者：张晓彤     
*完成日期：2016年11月25日  
*问题描述：判断给定的二叉树是否是二叉排序树。  
  
*/   

#include <stdio.h>    
#include <malloc.h>    
#define MaxSize 100    
typedef int KeyType;                    //定义关键字类型    
typedef char InfoType;    
typedef struct node                     //记录类型    
    
    KeyType key;                        //关键字项    
    InfoType data;                      //其他数据域    
    struct node *lchild,*rchild;        //左右孩子指针    
 BSTNode;    
int path[MaxSize];                      //全局变量,用于存放路径    
void DispBST(BSTNode *b);               //函数说明    
int InsertBST(BSTNode *&p,KeyType k)    //在以*p为根节点的BST中插入一个关键字为k的节点    
    
    if (p==NULL)                        //原树为空, 新插入的记录为根节点    
        
        p=(BSTNode *)malloc(sizeof(BSTNode));    
        p->key=k;    
        p->lchild=p->rchild=NULL;    
        return 1;    
        
    else if (k==p->key)    
        return 0;    
    else if (k<p->key)    
        return InsertBST(p->lchild,k);  //插入到*p的左子树中    
    else    
        return InsertBST(p->rchild,k);  //插入到*p的右子树中    
    
BSTNode *CreatBST(KeyType A[],int n)    
//由数组A中的关键字建立一棵二叉排序树    
    
    BSTNode *bt=NULL;                   //初始时bt为空树    
    int i=0;    
    while (i<n)    
        InsertBST(bt,A[i++]);       //将A[i]插入二叉排序树T中    
    return bt;                          //返回建立的二叉排序树的根指针    
    
    
void DispBST(BSTNode *bt)    
//以括号表示法输出二叉排序树bt    
    
    if (bt!=NULL)    
        
        printf("%d",bt->key);    
        if (bt->lchild!=NULL || bt->rchild!=NULL)    
            
            printf("(");    
            DispBST(bt->lchild);    
            if (bt->rchild!=NULL) printf(",");    
            DispBST(bt->rchild);    
            printf(")");    
            
        
    
    
/*  
int JudgeBST(BSTNode *bt)为判断一个树是否为排序二叉树设计的算法的实现  
*/    
KeyType predt=-32767; //predt为全局变量,保存当前节点中序前趋的值,初值为-∞    
int JudgeBST(BSTNode *bt)   //判断bt是否为BST    
    
    int b1,b2;    
    if (bt==NULL)    
        return 1;    //空二叉树是排序二叉树    
    else    
        
        b1=JudgeBST(bt->lchild);   //返回对左子树的判断，非排序二叉树返回0，否则返回1    
        if (b1==0 || predt>=bt->key)  //当左子树非排序二叉树，或中序前趋（全局变量）大于当前根结点时    
            return 0;    //返回“不是排序二叉树”    
        predt=bt->key;   //记录当前根为右子树的中序前趋    
        b2=JudgeBST(bt->rchild);   //对右子树进行判断    
        return b2;    
        
    
    
int main()    
    
    BSTNode *bt;    
    int a[]= 43,91,10,18,82,65,33,59,27,73,n=10;    
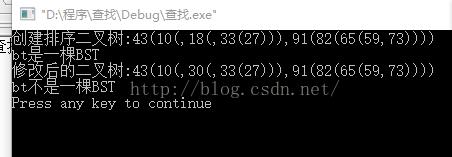
    printf("创建排序二叉树:");    
    bt=CreatBST(a,n);    
    DispBST(bt);    
    printf("\\n");    
    printf("bt%s\\n",(JudgeBST(bt)?"是一棵BST":"不是一棵BST"));    
    bt->lchild->rchild->key = 30;  //搞个破坏！    
    printf("修改后的二叉树:");    
    DispBST(bt);    
    printf("\\n");    
    printf("bt%s\\n",(JudgeBST(bt)?"是一棵BST":"不是一棵BST"));    
    return 0;    
    

运行结果：

知识点总结

这个程序说白了就是判断这个二叉树是否按折半查找的方式排列的数字。宏观来说很简单，就是拿二叉树中所有“小树”的根节点与其左右节点比较。

学习心得

知原理的题一定一定要好好做，在纸上的实践更容易明白细的知识点。