MIT 18.02 多变量微积分总结(Part I)
Posted Xurtle
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MIT 18.02 多变量微积分总结(Part I)相关的知识,希望对你有一定的参考价值。
引言
这篇文章是对 Multivariable Calculus 课程的知识点总结。
Dot Product
Because the dot product results in a scalar, it is also called the scalar product.
algebraic view of dot product
给定两个向量 a⃗ =⟨a1,a2,a3⟩ , b⃗ =⟨b1,b2,b3⟩ ,它们的点积定义如下:
a⃗ ⋅b⃗ =a1b1+a2b2+a3b3
properties of dot product
下面属性的证明大部分都是一些代数计算,根据点积的 algebraic view,你可以很轻松地证明出来。
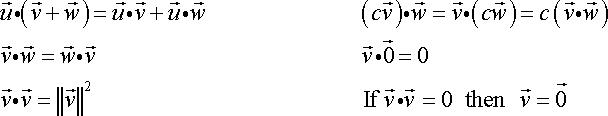
geometric view of dot product
下面定理用 The Law of Cosines 来证明,详细步骤参考:Dot Product
a⃗ ⋅b⃗ =|a⃗ ||b⃗ |cos(θ)
这个公式通常不是用来计算点积,而是找出2个向量之间的角。有了这个公式,点积可以让我们很容易地判断出2个向量是否 perpendicular or parallel. (When two vectors are perpendicular to each other we say they are orthogonal.)
Now, if two vectors are orthogonal then we know that the angle between them is 90 degrees:
a⃗ ⋅b⃗ =0
Likewise, if two vectors are parallel then the angle between them is either 0 degrees (pointing in the same direction) or 180 degrees (pointing in the opposite direction):
a⃗ ⋅b⃗ =|a⃗ ||b⃗ | (θ=0)a⃗ ⋅b⃗ =−|a⃗ ||b⃗ | (θ=180)
Projections
下面2幅图是 the projection of b⃗ onto a⃗ , denoted by proja⃗ b⃗
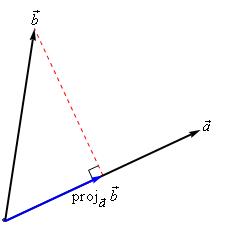
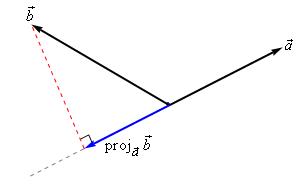
There is an nice formula for finding the projection of b⃗ onto a⃗ . Here it is,
proja⃗ b⃗ =a⃗ ⋅b⃗ |a⃗ |2a⃗
Note that we also need to be very careful with notation here. The projection of a⃗ onto