刷题之前这些东西你了解吗？

Posted 2022-12-10 小王子jvm

说在前头：本文主要参考算法小抄写的，原作者在这：https://labuladong.gitbook.io/algo/
但是这个网站经常打不开，我也不懂。。。
另外，本文没有列出所有例子，只挑选了部分，更多的请参考原作者。

框架思维和套路

数据结构的存储方式只有两种：数组（顺序存储）和链表（链式存储）

这句话一定要明白，不论后面的什么二叉树，栈，队列啥的，都是基于这两种东西深入。

对于任何数据结构，其基本操作无非遍历 + 访问，再具体一点就是：增删查改。

如何遍历 + 访问？

我们仍然从最高层来看，各种数据结构的遍历 + 访问无非两种形式：线性的和非线性的。

线性就是 for/while 迭代为代表，非线性就是递归为代表。再具体一步，无非以下几种框架。

数组的遍历方式

void traverse(int[] arr) 
  for (int i = 0; i < arr.length; i++) 
    // 迭代访问 arr[i]
  

所有的数组都可以使用这样的方式去遍历。

链表的遍历方式

/* 基本的单链表节点 */
class ListNode 
    int val;
    ListNode next;


//使用线性的遍历方式
void traverse(ListNode head) 
    for (ListNode p = head; p != null; p = p.next) 
        // 迭代访问 p.val
    


//递归遍历方式
void traverse(ListNode head) 
    // 递归访问 head.val
    traverse(head.next)

二叉树的遍历方式

/* 基本的二叉树节点 */
class TreeNode 
    int val;
    TreeNode left, right;


void traverse(TreeNode root) 
    traverse(root.left)
    traverse(root.right)

就是这个基本的东西，就可以完成前序，中序，后序遍历！

二叉树框架可以扩展为 N 叉树的遍历框架：

class TreeNode 
    int val;
    TreeNode[] children;


//迭代 + 递归
void traverse(TreeNode root) 
    for (TreeNode child : root.children) 
        traverse(child)
    

所谓框架，就是套路。不管增删查改，这些代码都是永远无法脱离的结构，你可以把这个结构作为大纲，根据具体问题在框架上添加代码就行了。

递归的理解

线性遍历很好理解，递归遍历就优点困难了。

写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要试图跳入递归。

递归的三要素：

明确函数想要干啥

要完成什么样的一件事，而这个，是完全由你自己来定义的。也就是说，我们先不管函数里面的代码什么，而是要先明白，你这个函数是要用来干什么。

例如：求一个数的阶乘，那么返回值就是需要的这个数的阶乘结果，参数就是需要被求的数

// 算 n 的阶乘(假设n不为0)
int f(int n)

寻找递归结束的条件

必须要找出递归的结束条件，不然的话，会一直调用自己，进入无底洞。也就是说，我们需要找出当参数为啥时，递归结束，之后直接把结果返回，请注意，这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

例如上面的例子：

// 算 n 的阶乘(假设n不为0)
int f(int n)
    if(n == 1)
        return 1;
    

但是，n=2的时候也是这个函数的结束条件，所以有：

// 算 n 的阶乘(假设n不为0)
int f(int n)
    if(n <= 2)
        return n;
    

找出函数的等价关系式

我们要不断缩小参数的范围，缩小之后，我们可以通过一些辅助的变量或者操作，使原函数的结果不变。

例如，f(n) 这个范围比较大，我们可以让 f(n) = n * f(n-1)。这样，范围就由 n 变成了 n-1 了，范围变小了，并且为了原函数f(n) 不变，我们需要让 f(n-1) 乘以 n。

说白了，就是要找到原函数的一个等价关系式，f(n) 的等价关系式为 n * f(n-1)，即f(n) = n * f(n-1)。

等价关系式的寻找，可以说是最难的一步了，找出了这个等价，继续完善我们的代码，我们把这个等价式写进函数里。如下：

// 算 n 的阶乘(假设n不为0)
int f(int n)
    if(n <= 2)
        return n;
    
    // 把 f(n) 的等价操作写进去
    return f(n-1) * n;

至此，递归三要素已经都写进代码里了，所以这个 f(n) 功能的内部代码我们已经写好了。

一个案例：剑指 Offer 10- II. 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

按照这个思路过来，第一步确定这个函数需要干什么。

一个N级台阶，这显然就是一个输入条件，共有多少中跳法，这个就是需要求的，也就是返回值，于是：

int f(int n)
    

这样一来，函数就有了。

第二步，找到结束的条件。台阶一共两种跳法，当n为1，自然就是只有一种跳法，n为2就有两种跳法，n等于3，恰好有三种跳法，后面的值就不是线性增长的了，所以结束条件也就有了：

int f(int n)
    if(n <= 3)
        return n;
    

第三步，找到等价关系式，也就是缩小这个参数值。跳一步，剩下n-1个，剩下的跳法有f(n-1)，跳两步，剩下的跳法有f(n-2)。所以f(n) = f(n-1) + f(n-2)。

于是有了这个：

int f(int n)
    if(n <= 3)
        return n;
    
    return f(n-1) + f(n-2)

哎，还是需要多刷题。

动态规划解题框架

动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。

求最值的核心问题就是把所有的结果都需要遍历出来，然后找到其中的最值。

但是这样存在很多问题，比如重叠子问题，暴力穷举会重复计算很多的值，所以需要一个备忘录来优化穷举的过程，避免不必要的计算。

而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的**「状态转移方程」**才能正确地穷举。

这里面最难的就是状态转移方程了。

斐波那契数列

一个简单的例子，理解一下这个过程

暴力递归，斐波那契数列的数学形式就是递归的，写成代码就是这样：

int fib(int N) 
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);

虽然简介，但是十分低效！

[ PS ]：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

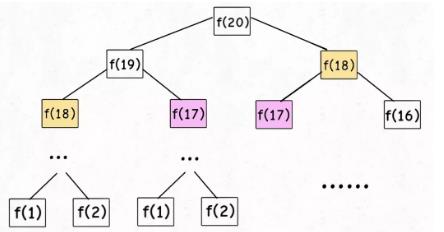
在这张递归树的图中，就可以看出有很多子问题被重复的计算。这也就是动态规划需要解决的第一个问题：重叠子问题。

带备忘录的递归解法

直到这个问题，怎么解决呢，既然是因为重叠的计算这些引起的，那就要想办法减少这些重复的计算，比如说每一个计算过的都给保存起来，这也就是造一个备忘录，下次计算前查这个备忘录中有没有这个值，然后再进行计算。一般使用一个数组来充当这个备忘录：

int fib(int N) 
    if (N < 1) return 0;
    int dp[] = new int[N+1];
    return reduce(dp,N);


//递归的三要素之一：明确函数目标
int reduce(int dp[],int n)
    //递归的三要素之二：结束条件
    if (n == 1 || n == 2) return 1;
    if(dp[n] != 0) return dp[n];	//不为0说明被计算过了
    
    //递归的三要素之三：递归等价关系式
    dp[n] = reduce(dp,n-1) + reduce(dp,n-2);
    return dp[n];

你会发现每次递归到一个已经被计算的值都会直接返回！

实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题的个数。

使用递归自顶向下可以解决这个问题，也可以使用迭代方式自底向上，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

dp 数组的迭代解法

在上一步使用数组存储中间元素后，发现，每个递归方法都会依赖（也就是要把这个表传进）这个表，那如果把他独立出来，也就是自底向上法：

int fib(int N) 
    if (N < 1) return 0;
    
    int dp[] = new int[N+1];
    dp[1] = dp[0] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];

你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。

这里，引出「状态转移方程」这个名词，实际上就是描述问题结构的数学形式：

把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，这就叫状态转移，仅此而已。

所有的操作都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性，它是解决问题的核心。很容易发现，其实状态转移方程直接代表着暴力解法。

上面这个问题你会发现，至始至终使用到就那么三个变量，所以，这里还可以优化一下：

int fib(int N) 
    if (N < 1) return 0;
    
    int a = b = 1;
    int sum = 0;
    for (int i = 3; i <= N; i++)
        sum = a + b;
        a = b;
        b = sum;
    
        
    return sum;

回溯法解题框架

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

伪代码框架：

result = [];	//保存结果
def backtrack(路径，选择列表)
    if(满足条件)
        result.add(路径);	//当前满足条件路径添加到集合
        return;	//跳出这个递归方法
    
    for(选择 ： 可选列表)
        做选择
        backtrack(路径，选择列表);
        撤销选择
    

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」

做选择和撤销选择，这也就是核心的部分。

全排列问题

n个不重复的数，全排列共有 n! 个。

[ PS ]：为了简单清晰起见，这次讨论的全排列问题不包含重复的数字。

比方说给三个数[1,2,3]，一般是这样：

先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……其实这就是回溯算法！

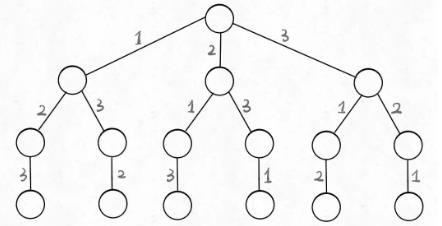
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。不妨把这棵树称为回溯算法的「决策树」，为啥说这是决策树呢，因为你在每个节点上其实都在做决策。

这个时候就可以来解释开局的几个名词解释了：

• 路径：我们选择的每一个点，比如第一次选择的2。

• 选择列表：第一个选择2后，剩下的1，3就是选择列表。

• 结束条件：到底没了，这就是结束条件

我们定义的backtrack函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其「路径」就是一个全排列。

再来看一下全排列代码：

List<List<Integer>> res = new LinkedList<>();
/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) 
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;


// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素
// 结束条件：nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) 
    // 触发结束条件
    if (track.size() == nums.length) 
        res.add(new LinkedList(track));
        return;
    

    for (int i = 0; i < nums.length; i++) 
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.removeLast();
    

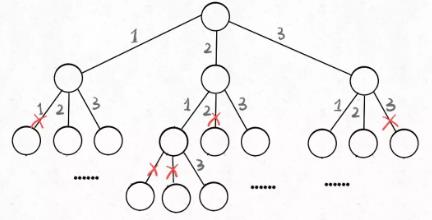
必须说明的是，不管怎么优化，都符合回溯框架，而且时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

BFS算法框架

BFS 出现的常见场景，问题的本质就是让你在一幅「图」中找到从起点start到终点target的最近距离，这个例子听起来很枯燥，但是 BFS 算法问题其实都是在干这个事儿。

代码框架：

//首先明确函数目标,给定起点和终点，返回路径
int BFS(Node start, Node target) 
    Queue<Node> q;  //核心数据结构，保存需要遍历的节点
    Set<Node> visited; //避免走回头路
    
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数
    
    while (q not empty) 	//只要队列不为空，说明还有选择可以尝试
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) 
            Node cur = q.poll();	//出队列
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) 
                    q.offer(x);
                    visited.add(x);
                
            
        
        /* 划重点：更新步数在这里 */
        step++;
    
    

BFS 的核心数据结构；cur.adj()泛指cur相邻的节点，比如说二维数组中，cur上下左右四面的位置就是相邻节点；visited的主要作用是防止走回头路，大部分时候都是必须的，但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要visited。

二叉树的最小高度

111. 二叉树的最小深度

首先明确起点和终点：

• 起点：也就是根节点
• 终点：也就是靠经起点的叶子节点（也就空节点）

所以判断结束的条件出来了：

if(cur.left == null && cur.right == null);	//表明到终点

然后按照框架思路进行改造：

int minDepth(TreeNode root) 
    if (root == null) return 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    // root 本身就是一层，depth 初始化为 1
    int depth = 1;

    while (!q.isEmpty()) 
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) 
            TreeNode cur = q.poll();
            /* 判断是否到达终点 */
            if (cur.left == null && cur.right == null) 
                return depth;
            /* 将 cur 的相邻节点加入队列 */
            if (cur.left != null)
                q.offer(cur.left);
            if (cur.right != null) 
                q.offer(cur.right);
        
        /* 这里增加步数 */
        depth++;
    
    return depth;

非递归版，还是比较好理解的。

二分法查找

几个最常用的二分查找场景：寻找一个数、寻找左侧边界、寻找右侧边界。而且，我们就是要深入细节，比如不等号是否应该带等号，mid 是否应该加一等等。

零、二分查找框架

代码框架：

int binarySearch(int[] nums, int target) 
    int left = 0, right = ...;

    while(...) 
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) 
            ...
         else if (nums[mid] < target) 
            left = ...
         else if (nums[mid] > target) 
            right = ...
        
    
    return ...;

整个代码的思路大概就是这个样子。

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。

其中...标记的部分，就是可能出现细节问题的地方，当你见到一个二分查找的代码时，首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。

另外声明一下，计算 mid 时需要防止溢出，代码中left + (right - left) / 2就和(left + right) / 2的结果相同，但是有效防止了left和right太大直接相加导致溢出。

寻找一个数（基本的二分搜索）

这个场景是最简单的，肯能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1

这里就直接给出代码了：

int binarySeacher(int nums[],int target)
    int left = 0;
    int right = nums.length - 1;
    
    while(left <= right)
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid;
        else if(nums[mid] < target)
            left = mid + 1;
        else if(nums[mid] > target)
            right = mid - 1;
        
    
    return -1;

这里需要解决的几个问题：

1. 为什么while循环的条件中是 <= ，而不是 <?

   因为初始化right的赋值是nums.length - 1，即最后一个元素的索引，而不是nums.length，这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间[left, right]，后者相当于左闭右开区间[left, right)，因为索引大小为nums.length是越界的。

2. 为什么left = mid + 1，right = mid - 1？我看有的代码是right = mid或者left = mid，没有这些加加减减，到底怎么回事，怎么判断？

   这也是二分查找的一个难点，刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即[left, right]。那么当我们发现索引mid不是要找的target时应该去搜索[left, mid-1]或者[mid+1, right]

3. 此算法有什么缺陷？

   给你有序数组nums = [1,2,2,2,3]，target为 2，此算法返回的索引是 2，没错。但是如果我想得到target的左侧边界，即索引 1，或者我想得到target的右侧边界，即索引 3，这样的话此算法是无法处理的。

寻找左侧边界的二分搜索

以下是最常见的代码形式，其中的标记是需要注意的细节：

int left_bound(int[] nums, int target) 
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; // 注意,上面例子为nums.length-1

    while (left < right)  // 注意
        int mid = (left +<
以上是关于刷题之前这些东西你了解吗？的主要内容，如果未能解决你的问题，请参考以下文章
 
 Redis这些知识你了解吗？
 leetcode刷题（128）——1575. 统计所有可行路径，动态规划解法
 LeetCode刷题之二叉树的前序遍历
 leetcode刷题（127）——1575. 统计所有可行路径，DFS解法
 [总结]数组
 冒泡排序这 2 个小技巧，你了解吗？