机器学习实战二:波士顿房价预测 Boston Housing
Posted 风信子的猫Redamancy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习实战二:波士顿房价预测 Boston Housing相关的知识,希望对你有一定的参考价值。
波士顿房价预测 Boston housing
这是一个波士顿房价预测的一个实战,上一次的Titantic是生存预测,其实本质上是一个分类问题,就是根据数据分为1或为0,这次的波士顿房价预测更像是预测一个连续值,当然这也是一个非常经典的机器学习案例Boston housing
如果想了解更多的知识,可以去我的机器学习之路 The Road To Machine Learning通道
目录
活动背景
波士顿房地产市场竞争激烈,而你想成为该地区最好的房地产经纪人。为了更好地与同行竞争,你决定运用机器学习的一些基本概念,帮助客户为自己的房产定下最佳售价。幸运的是,你找到了波士顿房价的数据集,里面聚合了波士顿郊区包含多个特征维度的房价数据。你的任务是用可用的工具进行统计分析,并基于分析建立优化模型。这个模型将用来为你的客户评估房产的最佳售价。
数据介绍


详细代码解释
导入Python Packages
首先导入需要的python包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
plt.style.use('ggplot')
%load_ext klab-autotime
读入数据 Read-In Data
将housing,csv读入
data = pd.read_csv('../data_files/2.Boston_housing/housing.csv')
data.info()
# No 属性 数据类型 字段描述x
# 1 CRIM Float 城镇人均犯罪率
# 2 ZN Float 占地面积超过2.5万平方英尺的住宅用地比例
# 3 INDUS Float 城镇非零售业务地区的比例
# 4 CHAS Integer 查尔斯河虚拟变量 (= 1 如果土地在河边;否则是0)
# 5 NOX Float 一氧化氮浓度(每1000万份)
# 6 RM Float 平均每居民房数
# 7 AGE Float 在1940年之前建成的所有者占用单位的比例
# 8 DIS Float 与五个波士顿就业中心的加权距离
# 9 RAD Integer 辐射状公路的可达性指数
# 10 TAX Float 每10,000美元的全额物业税率
# 11 PTRATIO Float 城镇师生比例
# 12 B Float 1000(Bk - 0.63)^ 2其中Bk是城镇黑人的比例
# 13 LSTAT Float 人口中地位较低人群的百分数
# 14 MEDV Float (目标变量/类别属性)以1000美元计算的自有住房的中位数

从这里可以看出来,数据一共有14个特征,并且没有缺失值,所以我们可以不用缺失值处理,真不错
从Package读取Boston数据
其实在我们的sklearn库中,就有波士顿房屋数据集,我们可以直接读取数据集
from sklearn.datasets import load_boston
dir(load_boston())
print(load_boston().DESCR)

这里也有对数据集详细的介绍,除此之外,我们还需要将数据集转化了类型,变为我们熟悉的pandas.core.frame.DataFrame,之后后面的操作就是一模一样的了
X = load_boston().data
y = load_boston().target
df = pd.DataFrame(X, columns=load_boston().feature_names)
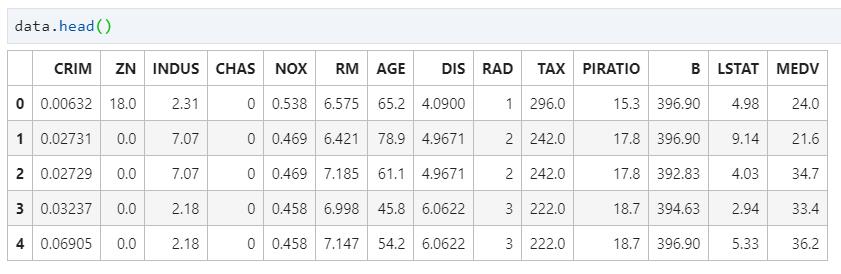
df.head()
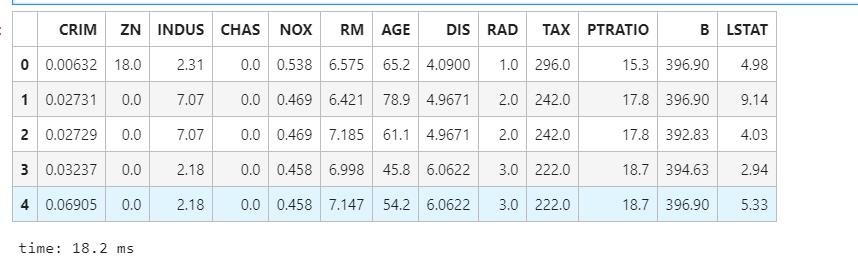
相关性检验
看看各个特征中是否有相关性,判断一下用哪种模型比较合适
plt.figure(figsize=(12,8))
sns.heatmap(data.corr(), annot=True, fmt='.2f', cmap='PuBu')
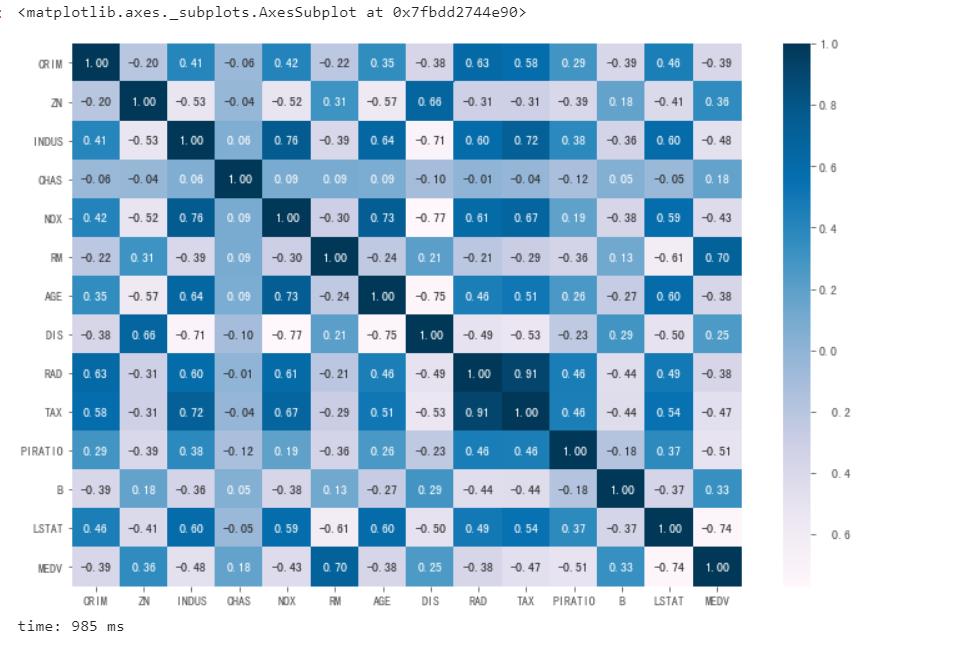
数据不存在相关性较小的属性,也不用担心共线性,所以我们可以用线性回归模型去预测
data.corr()['MEDV'].sort_values()
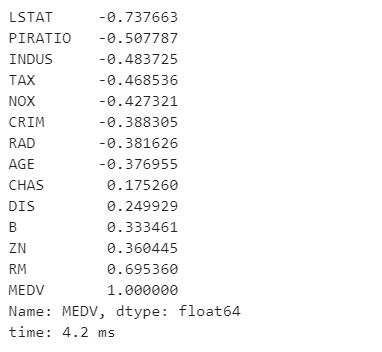
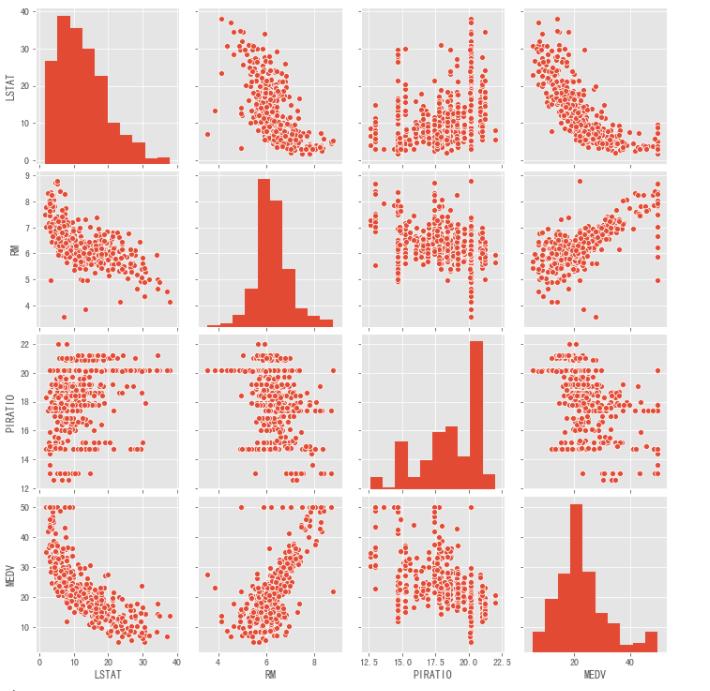
多变量研究
尝试了解因变量和自变量、自变量和自变量之间的关系
sns.pairplot(data[["LSTAT","RM","PIRATIO","MEDV"]])
划分训练集和测试集
由于数据没有null值,并且,都是连续型数据,所以暂时不用对数据进行过多的处理,不够既然要建立模型,首先就要进行对housing分为训练集和测试集,取出了大概百分之20的数据作为测试集,剩下的百分之70为训练集
X ,y = data[data.columns.delete(-1)], data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=888)
查看训练集和测试集的维度
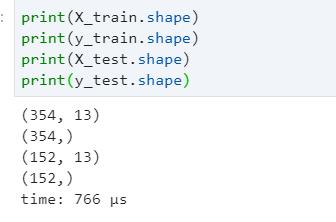
建立线性回归模型
首先,我利用线性回归模型对数据进行训练,并预测测试集数据,对于具体的线性回归的介绍,可以参考Linear Regression Machine Learning

linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
coef = linear_model.coef_#回归系数
line_pre = linear_model.predict(X_test)
print('SCORE::.4f'.format(linear_model.score(X_test, y_test)))
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test, line_pre))))
coef
根据结果来看,预测的score为76%左右,然后均方误差RMSE大约是4.5,为了更好的看出预测数据的问题,我想试着可视化一下
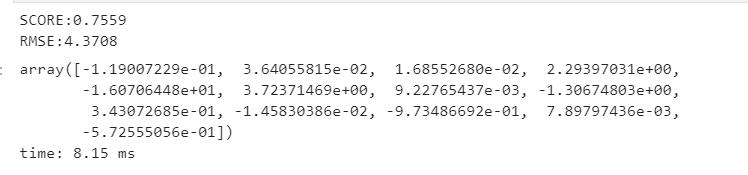
df_coef = pd.DataFrame()
df_coef['Title'] = data.columns.delete(-1)
df_coef['Coef'] = coef
df_coef
这是线性回归的相关系数
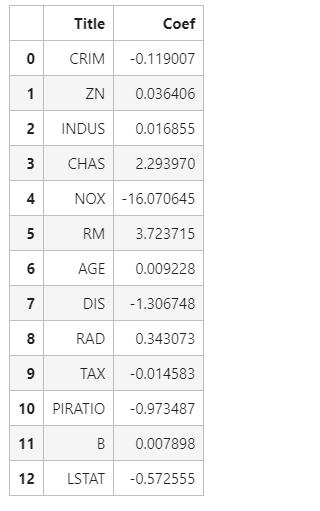
hos_pre = pd.DataFrame()
hos_pre['Predict'] = line_pre
hos_pre['Truth'] = y_test
hos_pre.plot(figsize=(18,8))

- 得出score为76%,从上图得知预测的房价整体偏小,在10-35这个区间预测结果较为准确,超过这个区间预测价格偏小,可进一步对原始数据离群值做处理。
- 数据比较干净,练习起来缺少特征工程部分的工作,而且是预测性模型,相比分类问题少了模型选择上的空间。
评价模型
在整个数据集上评价模型
plt.scatter(y_test, line_pre,label='y')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4,label='predicted')

然后在整个数据集中评价模型
line_pre_all = linear_model.predict(X) #预测值
print('SCORE::.4f'.format(linear_model.score(X,y)))
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y, line_pre_all))))
hos_pre_all = pd.DataFrame()
hos_pre_all['Predict'] = line_pre_all
hos_pre_all['Truth'] = y
hos_pre_all.plot(figsize=(18,8))

plt.scatter(y, line_pre_all,label='y')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4,label='predicted')
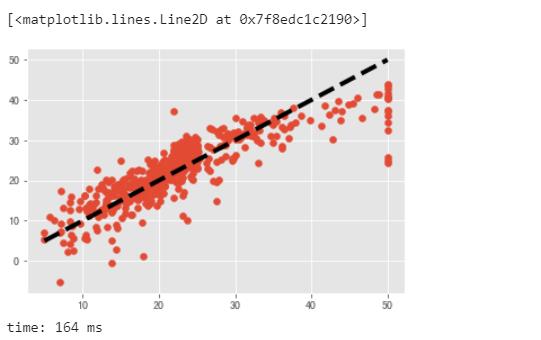
由以上分析可知,模型在整个数据集中的评分比在测试集中要低
进一步探索和模型改进
- 尝试使用相关性最高的3个特征量重建模型,并与原模型进行比较
- 尝试使用其它多种算法分别建立模型,并比较模型
特征选择重建模型
首先我尝试相关性最高的三个特征重建模型,去与原模型比较一下
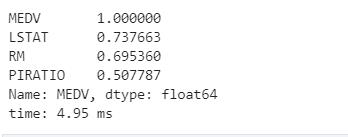
data.corr()['MEDV'].abs().sort_values(ascending=False).head(4)
由此我们得出了三个相关性最高的特征,我们将其作为自变量去建立模型
X2 = np.array(data[['LSTAT','RM','PIRATIO']])
X2_train, X2_test, y_train, y_test = train_test_split(X2, y, random_state=1,test_size=0.2)
linear_model2 = LinearRegression()
linear_model2.fit(X2_train,y_train)
print(linear_model2.intercept_)
print(linear_model2.coef_)
line2_pre = linear_model2.predict(X2_test) #预测值
print('SCORE::.4f'.format(linear_model2.score(X2_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test, line2_pre))))#RMSE(标准误差)
我们可以得到,对于预测测试集的数据的得分score明显是没有开始的线性回归模型1高的,然后我们再看看,在整个数据集中它的表现

line2_pre_all = linear_model2.predict(X2) #预测值
print('SCORE::.4f'.format(linear_model2.score(X2, y)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y, line2_pre_all))))#RMSE(标准误差)

这样比较下来,第一个模型达到的分数,即使在整个数据集中73%,但是这个模型的得分大约是67.6%,由此可以得出,第一个模型还是比这个模型优的,接下来就需要尝试更多的模型了
数据标准化
数据集的 标准化 对scikit-learn中实现的大多数机器学习算法来说是 常见的要求 。如果个别特征或多或少看起来不是很像标准正态分布(具有零均值和单位方差),那么它们的表现力可能会较差。
所以我这里首先对数据进行了一个标准化处理
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
X_train = ss_x.fit_transform(X_train)
X_test = ss_x.transform(X_test)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(y_train.values.reshape(-1, 1))
y_test = ss_y.transform(y_test.values.reshape(-1, 1))
模型优化和改进
接下来我就开始尝试多种模型,希望尝试的模型有对我的算法有帮助
X ,y = data[data.columns.delete(-1)], data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=9)
GradientBoosting(梯度提升)
from sklearn import ensemble
#params = 'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1,'learning_rate': 0.01, 'loss': 'ls'
#clf = ensemble.GradientBoostingRegressor(**params)
clf = ensemble.GradientBoostingRegressor()
clf.fit(X_train, y_train)
clf_pre=clf.predict(X_test) #预测值
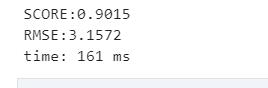
print('SCORE::.4f'.format(clf.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test, clf_pre))))#RMSE(标准误差)
Lasso 回归 (Least Absolute Shrinkage and Selection Operator)
Lasso也是惩罚其回归系数的绝对值。
与岭回归不同的是,Lasso回归在惩罚方程中用的是绝对值,而不是平方。这就使得惩罚后的值可能会变成0
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(X_train,y_train)
y_predict_lasso = lasso.predict(X_test)
r2_score_lasso = r2(y_test,y_predict_lasso)
print('SCORE::.4f'.format( lasso.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test,y_predict_lasso))))#RMSE(标准误差)
print('Lasso模型的R-squared值为:',r2_score_lasso)
ElasticNet 回归
ElasticNet回归是Lasso回归和岭回归的组合
enet = ElasticNet()
enet.fit(X_train,y_train)
y_predict_enet = enet.predict(X_test)
r2_score_enet = r2(y_test,y_predict_enet)
print('SCORE::.4f'.format( enet.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test,y_predict_enet))))#RMSE(标准误差)
print("ElasticNet模型的R-squared值为:",r2_score_enet)
Support Vector Regression (SVR)
from sklearn.linear_model import ElasticNet
from sklearn.svm import SVR
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.metrics import r2_score as r2, mean_squared_error as mse, mean_absolute_error as mae
def svr_model(kernel):
svr = SVR(kernel=kernel)
svr.fit(X_train, y_train)
y_predict = svr.predict(X_test)
# score(): Returns the coefficient of determination R^2 of the prediction.
print(kernel,' SVR的默认衡量评估值值为:', svr.score(X_test,y_test))
print(kernel,' SVR的R-squared值为:', r2(y_test, y_predict))
print(kernel,' SVR的均方误差(mean squared error)为:',mse(y_test, y_predict))
print(kernel,' SVR的平均绝对误差(mean absolute error)为:',mae(y_test,y_predict))
# print(kernel,' SVR的均方误差(mean squared error)为:',mse(scalery.inverse_transform(y_test), scalery.inverse_transform(y_predict)))
# print(kernel,' SVR的平均绝对误差(mean absolute error)为:',mae(scalery.inverse_transform(y_test),scalery.inverse_transform(y_predict)))
return svr
linear 线性核函数
linear_svr = svr_model(kernel='linear')

poly 多项式核
poly_svr = svr_model(kernel='poly')

rbf(Radial Basis Function) 径向基函数
rbf_svr = svr_model(kernel='rbf')

SVM(支持向量机)回归-- 线性核
from sklearn.svm import SVR
linear_svr = SVR(kernel="linear")
linear_svr.fit(X_train, y_train)
linear_svr_pre = linear_svr.predict(X_test)#预测值
print('SCORE::.4f'.format(linear_svr.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test, linear_svr_pre))))#RMSE(标准误差)

SVM(支持向量机)回归-- 多项式核
在使用SVM回归-- 多项式核的时候,首先要对数据进行一个标准化处理
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
X_train = ss_x.fit_transform(X_train)
X_test = ss_x.transform(X_test)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(y_train.values.reshape(-1, 1))
y_test = ss_y.transform(y_test.values.reshape(-1, 1))
再进行建立模型来预测
poly_svr = SVR(kernel="poly")
poly_svr.fit(X_train, y_train)
poly_svr_pre = poly_svr.predict(X_test)#预测值
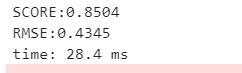
print('SCORE::.4f'.format(poly_svr.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test, poly_svr_pre))))#RMSE(标准误差)
决策树回归
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X_train, y_train)
tree_reg_pre = tree_reg.predict(X_test)#预测值
print('SCORE::.4f'.format( tree_reg.score(X_test, y_test)))#模型评分
print('RMSE::.4f'.format(np.sqrt(mean_squared_error(y_test,tree_reg_pre))))#RMSE(标准误差)

最后我们会发现,利用GBDT的得分居然高达90,这是我们得到最优的一个模型了,其次就是SVR回归的多项式核,也大概达到了85,其他的并没有线性回归那么优,所以对于波士顿房价预测来说,利用GBDT是最好的,这是迄今为止我遇到最好的模型
总结
- 可以发现,如果要用Gradient Boosting 算法的话,在sklearn包里调用是非常方便的,几行代码即可完成,大部分的工作是在数据特征提取
- 数据分析过程中,特征设计是最重要的,现在kaggle竞赛很流行使用GBDT(梯度提升决策树Gradient Boosted Decision Tree) 算法,数据分析结果的优劣其实主要在特征上,行业中做项目也是如此
- 不断的在研究数据中培养对数据的敏感度十分重要
每日一句
Never had to laugh at other people.(没经历过才笑别人的疤)
如果需要数据和代码,可以自提
- 路径1:我的gitee
- 路径2:百度网盘
链接:https://pan.baidu.com/s/1uA5YU06FEW7pW8g9KaHaaw
提取码:5605
以上是关于机器学习实战二:波士顿房价预测 Boston Housing的主要内容,如果未能解决你的问题,请参考以下文章
机器学习之路: python 回归树 DecisionTreeRegressor 预测波士顿房价
机器学习之利用线性回归预测波士顿房价和可视化分析影响房价因素实战(python实现 附源码 超详细)
机器学习之路: python 线性回归LinearRegression, 随机参数回归SGDRegressor 预测波士顿房价