板子树

Posted 2022-12-10 绀香零八

🌳板子集锦

文章目录

• 一. 前序、后序、层序+中序-->?
• • 1. 前序+中序
  • • -->后序
    • -->层序
  • 2. 后序+中序
  • • -->前序
    • -->层序
• 二. 并查集
• • 1.定义
  • 2.基本操作
  • • 1）初始化
    • 2）查找
    • • 路径压缩
    • 3）合并
• 三. 树的遍历应用

一. 前序、后序、层序+中序–>?

都是向柳神学的~~
都是一个套路，要求转换成什么，就把函数名换成什么，更改递归函数的根结点位置、当前左、右子树在中序遍历的start、end位置，若要转换成层序，增加一个变量index记录下标即可

1. 前序+中序

–>后序

暂时未遇到，遇到再总结

–>层序

L2-011 玩转二叉树 (25分)

void level(int root,int start,int end,int index)
	if(start>end) return;
	int k;
	for(k=start;k<end;k++) if(in[k]==pre[root]) break;
	ans[index] = pre[root];
	level(root+1,start,k-1,2*index+2);
	level(root+1+k-start,k+1,end,2*index+1);

2. 后序+中序

–>前序

4-15 根据后序和中序遍历输出先序遍历 (15分)

void pre(int root,int start,int end)
	if(start>end) return;
	int k;
	for(k=start;k<end;k++)
		if(in[k]==post[root]) break;
	cout << " " << post[root];	
	pre(root-1-end+k,start,k-1);
	pre(root-1,k+1,end);

–>层序

中文版题目    L2-006 树的遍历 (25分)
英文版题目    1020 Tree Traversals (25分)

void level(int root,int start,int end,int index)
	if(start>end) return;
	int k;
	for(k=start;k<end;k++) if(in[k]==post[root]) break;
	ans[index] = post[root];
	level(root-1-end+k,start,k-1,2*index+1);
	level(root-1,k+1,end,2*index+2);

二. 并查集

L2-024 部落 (25分)

1.定义

并查集是一种维护集合的数据结构，“并”Union、“查”Find、“集”Set，支持以下操作：
· 合并：合并两个集合
· 查找：判断两个元素是否在一个集合
使用一个数组实现

int father[N];  //father[i]表示元素i的父亲结点，1<=i<=N

父亲结点本身也是这个集合内的元素,并且如果father[i]=i;说明结点i是该集合的根结点，对同一个集合来说只有一个根节点，将其作为所属集合的标识
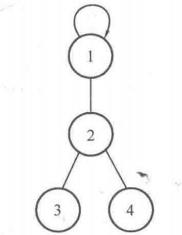
eg.👇图

father[1] = 1;  //1的父亲结点是自己，是根节点
father[2] = 1;
father[3] = 2;
father[4] = 2;

2.基本操作

1）初始化

初始状态每个元素都是一个独立的集合

void init(int N)
	for(int i=1;i<=N;i++)
		father[i] = i;
	 

2）查找

规定同一个集合只能有一个根结点，因此查找操作就是对给定的结点寻找其根结点的过程。
思路：反复寻找父亲结点，直到找到根结点father[i]=i;的结点

//findFather函数返回元素x所在的集合的根结点
//递推
int findFather(int x)
	while(x!=father[x])
		x = father[x];
	
	return x;


//递归
int findFather(int x)
	if(x==father[x]) return x;
	else return findFather(father[x]);

路径压缩

👆查找函数未优化，极端情况下效率较低。如👇图，给出的元素数量很多且形成一条链，并查集退化，查找效率极低。

· 解决方法： 想办法把当前查询节点路径上的所有结点的父亲都指向根结点 示意图👇查找的时候不需要一直回溯找父亲，查询复杂度降为O(1)

转化步骤：
1.按原先的写法从给定的结点不断获得其父亲结点而最终到达根结点获得x的根结点r
2.重新从x开始走一遍寻找根结点的过程，把路径上经过的所有结点的父亲全部改为根结点r

//递推
int findFather(int x)
	int a = x;  //由于x在下面的while中会变成根结点，先保存原来x
	while(x!=father[x])  //寻根结点
		x = father[x];
	  //x现在存的是根结点
	while(a!=father[a])  //把路径上的所有结点的father都改成根结点
		int z = a;  //因为a要被father[a]覆盖，先保存a的值以修改father[a]
		a = father[a];  //a回溯父亲结点
		father[z] = x;  //将原先a结点的父亲改为根结点
	
	return x;


//递归
int findFather(int x)
	if(x==father[x]) return x;  //找到根结点
	else
		int F = findFather(father[x]);  //递归寻找father[v]根结点F
		father[v] = F;  //将根结点F赋给father[v]
		return F;  //返回根结点F
	

3）合并

把两个集合合并成一个
· 思路： 先判断两个元素是否属于同一个集合，只有当两个元素属于不同集合时才合并，将其中一个集合的根节点的父亲指向另一个集合的根结点

void Union(int a,int b)
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA!=faB)
		father[faA] = faB;
	

· 误区： 不可以将合并语句写成father[a] = b;如👇图

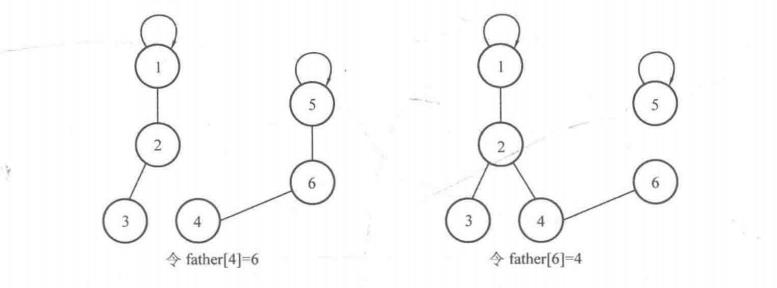
· 性质： 在合并过程中，只对两个不同的集合进行合并，如果两个元素在相同的集合中，那么就不会对他们操作。保证在同一个集合中一定不会产生环，即并查集产生的每一个集合都是一棵树

三. 树的遍历应用

有空再补~~