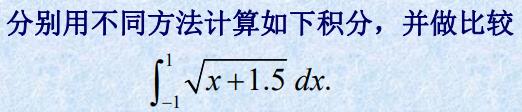《数值分析》-- 高斯求积公式

Posted 2022-12-10 胜天半月子

文章目录

• 概述
• 一、高斯型求积公式的一般理论
• • 1.1 高斯型求积公式和高斯点
  • 1.2 高斯点的特征
• 二、常用的高斯求积公式⭐
• • 2.1 高斯-勒让德求积公式（ Gauss-Legendre ）
  • 2.2 高斯-切比雪夫求积公式（ Gauss-Chebyshe）
• 总结

---

概述

• 问题
  那么，在节点个数一定的情况下，是否可以在[a，b]上自由选择节点的位置，使求积公式的精度提得更高？
  
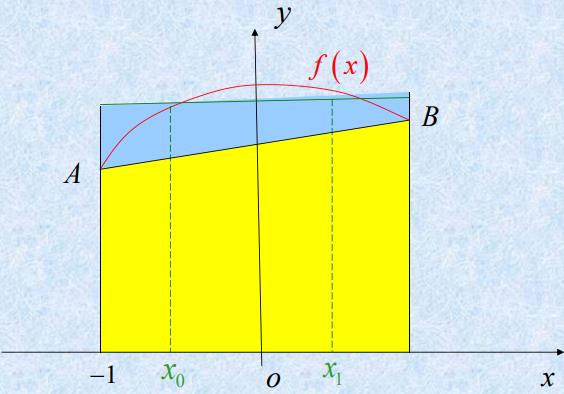
• 例题
  
  
  

---

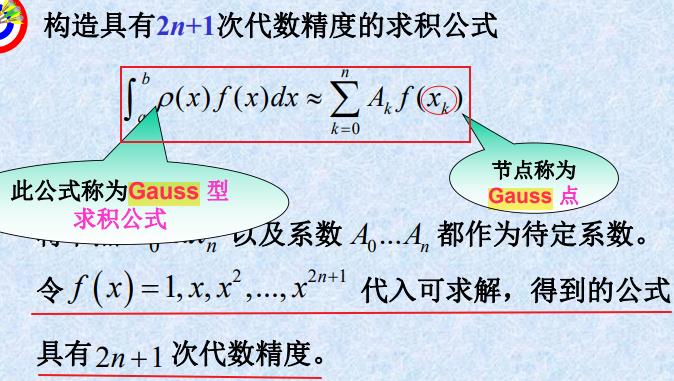
一、高斯型求积公式的一般理论

• 一般理论
  

1.1 高斯型求积公式和高斯点

习题

1.2 高斯点的特征

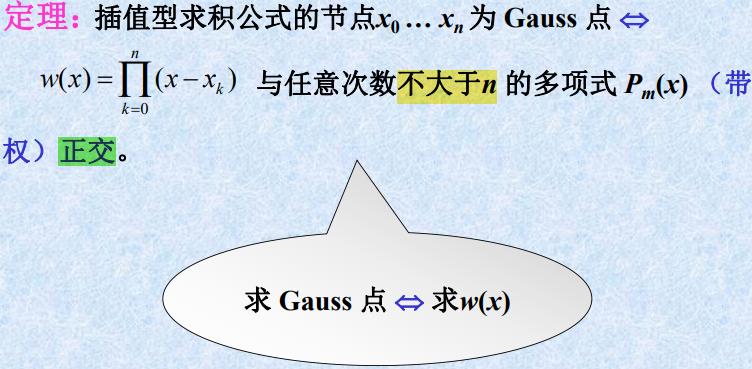
• 利用正交多项式构造高斯求积公式
  
  习题

---

二、常用的高斯求积公式⭐

2.1 高斯-勒让德求积公式（ Gauss-Legendre ）

• 概念
  勒让德多项式
  

1. Legendre 多项式族：
   
   低阶Legendre多项式
   
2. 高斯-勒让德求积公式（G-L求积公式）⭐
   
   
   
   

• 总结
  
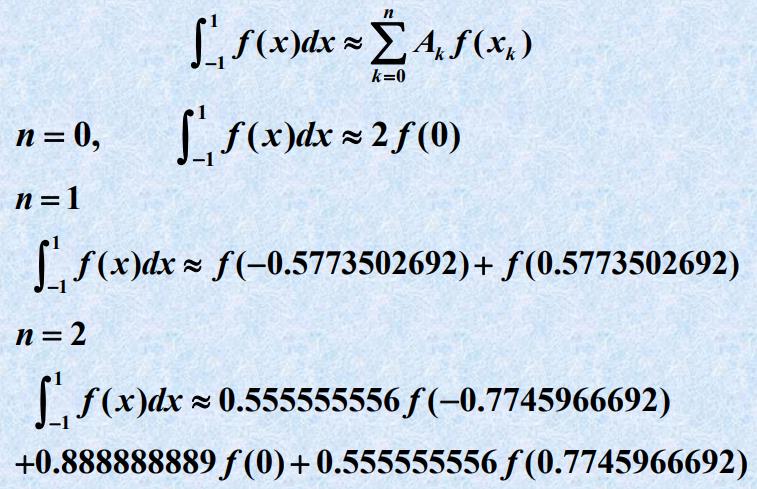
  习题

3. 一般有界区间[a, b]上的高斯-勒让德求积公式
   （G-L求积公式）
   目的转换区间到 [-1,1] :
   
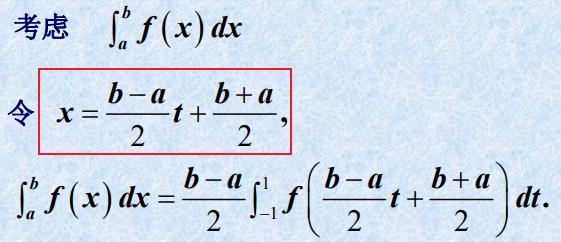
   习题

2.2 高斯-切比雪夫求积公式（ Gauss-Chebyshe）

切比雪夫多项式

• 截断误差
  

---

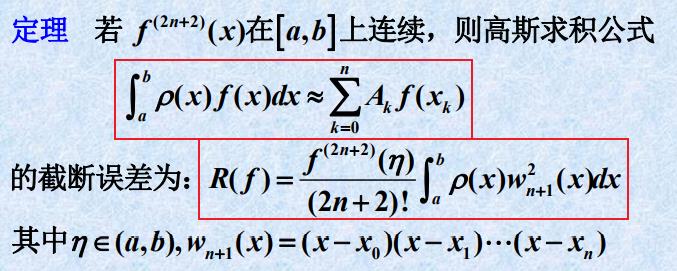
总结

• 例题

1. 
   用待定系数法构造高斯求积公式:
   

• 问题
  为什么2点Gauss公式有应该有三次代数精度？

一般n+1个节点的求积公式的代数精度最高为2n+1次

2. 
   

• 详细过程
  

3. 
   

• 详细过程
  
  
• 例题

1. 
   利用正交多项式构造高斯求积公式:
   
   
   

• 例题

1. 
   
   

• 公式回忆

1. 复合梯形公式
   
   三个点：$T2$
   五个点：$T4$
2. Simpson公式
   
3. 三个点的高斯-勒让德求积公式
   

• 例题

1. 
   

• 公式
  

2. 
   

• 两点高斯-勒让德求积公式
  

---

• 例题

1.