最优化——三点二次插值法（MATLAB实现）

Posted 2022-12-09 FILWY_M

算法流程框图

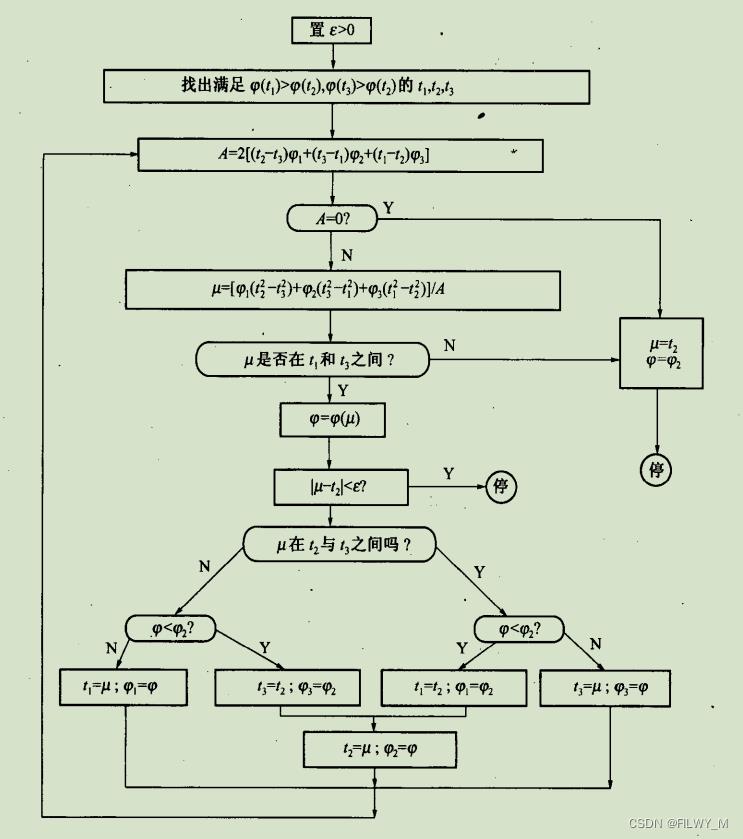
例题

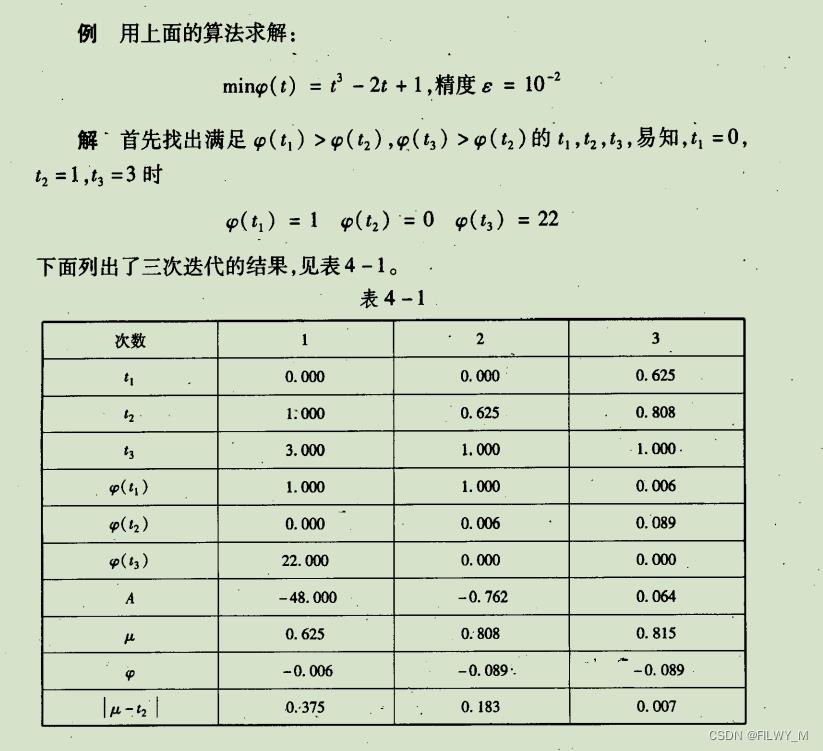
MATLAB实现代码

clc
clear
close all

epsilion = 0.01;

t1 = 0;
t2 = 1;
t3 = 3;

f1 = f(t1);
f2 = f(t2);
f3 = f(t3);

cnt = 1;

while true
    fprintf("第 %d 次：\\n", cnt);
    cnt = cnt + 1;
    disp(t1);
    disp(t2);
    disp(t3);
    disp(f1);
    disp(f2);
    disp(f3);
    A = fa(t1,t2,t3,f1,f2,f3);
    disp(A)
    if(A == 0)
        mu = t2;
        ff = f2;
        break
    end
    mu = fmu(t1,t2,t3,f1,f2,f3,A);
    disp(mu);
    if mu > t3 || mu < t1
        mu = t2;
        ff = f2;
        break
    end
    ff = f(mu);
    disp(ff);
    disp(abs(mu - t2));
    if(abs(mu - t2) < epsilion)
        break;
    end
    if mu >= t2 && mu <= t3
        if ff < f2
            t1 = t2;
            f1 = f2;
            t2 = mu;
            f2 = ff;
        else
            t3 = mu;
            f3 = ff;
        end
    else
        if ff < f2
            t3 = t2;
            f3 = f2;
            t2 = mu;
            f2 = ff;
        else
            t1 = mu;
            f1 = ff;
        end
    end
end

function f = f(t)

%f = (t - 0.05)^2;
f = (t^3 - 2*t + 1);

end

function A=fa(t1,t2,t3,f1,f2,f3)

A = 2*((t2-t3)*f1 + (t3-t1)*f2 + (t1-t2)*f3);

end

function mu = fmu(t1,t2,t3,f1,f2,f3,A)

mu = ((t2^2-t3^2)*f1 + (t3^2-t1^2)*f2 + (t1^2-t2^2)*f3) / A;

end

输出结果

第 1 次：
     0

     1

     3

     1

     0

    22

   -48

   0.625000000000000

  -0.005859375000000

   0.375000000000000

第 2 次：
     0

   0.625000000000000

     1

     1

  -0.005859375000000

     0

  -0.761718750000000

   0.807692307692308

  -0.088472917614929

   0.182692307692308

第 3 次：
   0.625000000000000

   0.807692307692308

     1

  -0.005859375000000

  -0.088472917614929

     0

  -0.064101082441966

   0.809288537549407

  -0.088535216985914

   0.001596229857100