强化学习介绍和马尔可夫决策过程详细推导

Posted 2022-12-08 搜索与推荐Wiki

强化学习系列学习笔记，结合《UCL强化学习公开课》、《白话强化学习与PyTorch》、网络内容，如有错误请指正，一起学习！

强化学习基本介绍

强化学习的中心思想是让智能体在环境中自我学习和迭代优化。

强化学习流程

强化学习的过程是一个反馈控制系统，其大概的一个流程图如下所示：

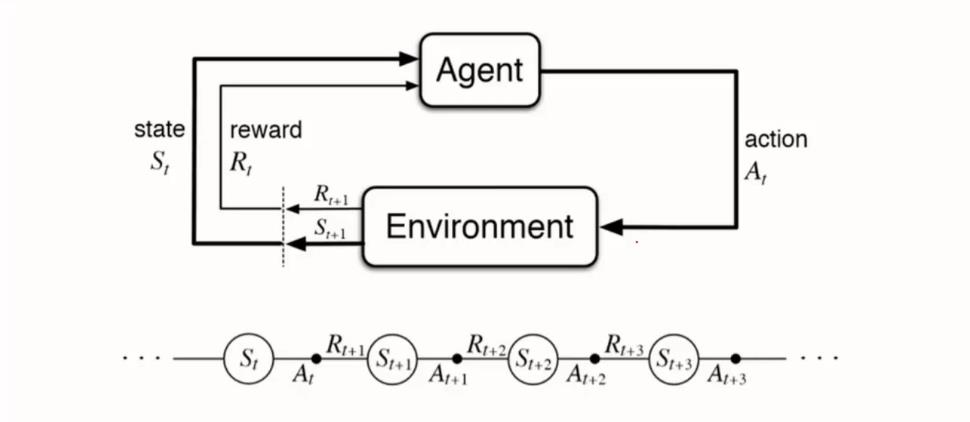
结合这张图，我们进行相关的概念解释和流程说明。首先图中涉及了几个概念，我们依次来看下是什么意思。

• Agent：或者称为“Brain”、大脑、智能体，是机器人的智能主体部分，也即我们要操控的对象
• Environment：指机器人所处的环境，客观存在的状态
• State：当前时刻下Agent所处的状态
• Reward：Agent在执行某个动作后获得的奖励
• Action：要执行的动作，Agent在结合当前所处的状态（State）和上一次执行动作（Action）之后获得的奖励（Reward）要在当前时刻下执行的动作

接着我们再去理解这个图，所表达的意思是：在当前状态（State，$S_t$）下，智能体（Agent）做了动作（Action，$A_t$）之后获得了奖励（Reward，$R_t$），其串行的流程为上图的下边部分。

强化学习与监督学习

机器学习从其学习方式上大体可以分为三类：

• 监督学习（supervised learning）
• 无监督学习（unsupervised learning）
• 强化学习（reinforcement learning）

监督学习是从有标签的数据集中进行模式和特征的学习，从而对新的样本进行预测，比如常见的分类、回归问题，还有推荐系统中的CTR预估。这种场景下label都是固定的，我们需要研究出一种固定的映射关系$y=f(x|\theta )$，以便于在新样本上发挥作用。

无监督学习则是对无标签的数据进行学习，比如常见的聚类就是典型的无监督学习算法。对比有监督学习，我们只知道样本即$x$，并不知道 也不需要知道$y$。

强化学习相较于监督学习和无监督学习，区别在于其是以不同建模方式或思考角度来解决问题，是一种方法论，其拥有了一套比较完整的处理数据、建模、训练、调优的套路。但是通过对强化学习流程的了解，你会发现强化学习和监督学习的思路有点类似，但是其标签（即$y$）是有时间上的延迟的，即先产生动作，再得到反馈。

强化学习的应用

对于强化学习大家印象最深的莫过于2016年AlphaGo击败 九段的围棋选手李在石，但其实强化学习也应用于社会中的各个场景，比如：

• 自动机器学习AutoML
• 决策服务（Decision Service）
• 推荐系统、广告系统
• 智能交通
• 机器人
• 计算机视觉
• 计算机系统
• 教育
• 金融
• 游戏
• 自动驾驶
• … …

在每年的各类计算机大会上发表的论文中，其实都可以看到强化学习的身影，由于笔者是专注于推荐系统的，所以主要关注的是：强化学习与推荐系统。

后续会在《结合论文看Youtube推荐系统中召回和排序的演进之路（下）篇》中介绍Youtube推荐系统与强化学习的结合应用，欢迎关注，目前已经更新（上）篇。

另外从事推荐系统相关工作的朋友，应该知道「多臂老虎机」，即Bandit类算法，其本质上也是一种自我博弈和反馈决策的过程，算是强化学习中比较好理解的算法和内容了，感兴趣的朋友可以看下面的2篇关于多臂老虎机的文章：

• EE和冷启动中的多臂老虎机问题
• LinUCB论文的思想解读、场景应用与痛点说明

马尔科夫决策过程

在前边的内容中提到了强化学习的决策过程，依赖于当前的状态的环境，但是实际的场景是非常复杂的，难以进行建模，因此对其进行了简化，即假设状态的转化是马尔科夫性，即转化到到下一个时刻的状态$s_{t+1}$ 仅仅和上一个状态$s_t$有关，与之前的状态无关。

因此我们先来了解一下马尔科夫的相关知识，再去了解马尔科夫决策过程（Markov Decision Process，MDP）。

马尔科夫链

什么是马尔科夫链呢？一个比较正式的定义为：设$x_t$表示随机变量$X$在离散时间$t$时刻的取值，若该变量随时间变化的转移概率仅依赖于它的当前值，即：
$$P(X_{t+1}=s_{j+1}|X_0=s_0,X_1=s_1,...,X_t=s_j)=P(X_{t+1}=s_{j+1}|X_t=s_t)$$
也就是状态转移概率仅依赖于前一个状态，称这个变量为马尔科夫变量，其中$s_0,s_1,...,s_j$为随机遍历$X$的可能状态，这个性质称为马尔科夫性质，具有马尔科夫性质的随机过程称为马尔科夫过程。

马尔科夫链则是满足马尔科夫性质的随机过程，在一段时间内随机变量$X$的取值序列（$X_0,X_1,...,X_n$）满足上述性质。

比如：一只青蛙呆在井底（$q=1$），一层一层的向上跳，到达第$i$层之后，它能跳上去的概率和跳不上去的概率（直接回到底层的概率）为：
$$\begin{array}{c}{q}_{i,i+1}=a_i\\ q_{i,1}=1-a_i\end{array}$$
也就是说，每一次这只青蛙站在比如第5层，下一次尝试能跳到第6层的概率都是一样的，跟这只青蛙历史上掉回底层多少次之类都是没有关系的，这就是一个马尔科夫过程。

马尔科夫过程是一个无记忆的随机过程，例如满足马尔科夫性质的状态一系列序列为：$S_1,S_2,S_3,...$

马尔科夫过程（Markov Process）的定义为：一个马尔科夫过程或者马尔科夫链由一个二元组构成：$（S,P）$

• $S$为有限的状态空间集，$s_i$表示时间步$i$的状态，其中$S=s_1,s_2,...,s_n$
• $P$为状态转移矩阵，$P_{s^{\prime }}=P[S_{s+1}=s^{\prime }|S_t=s]$

又比如把一个人的上课学习过程当作是一个简单的马尔科夫过程（例子来源：https://www.jianshu.com/p/fb33231ac3a8 ），如下图所示：

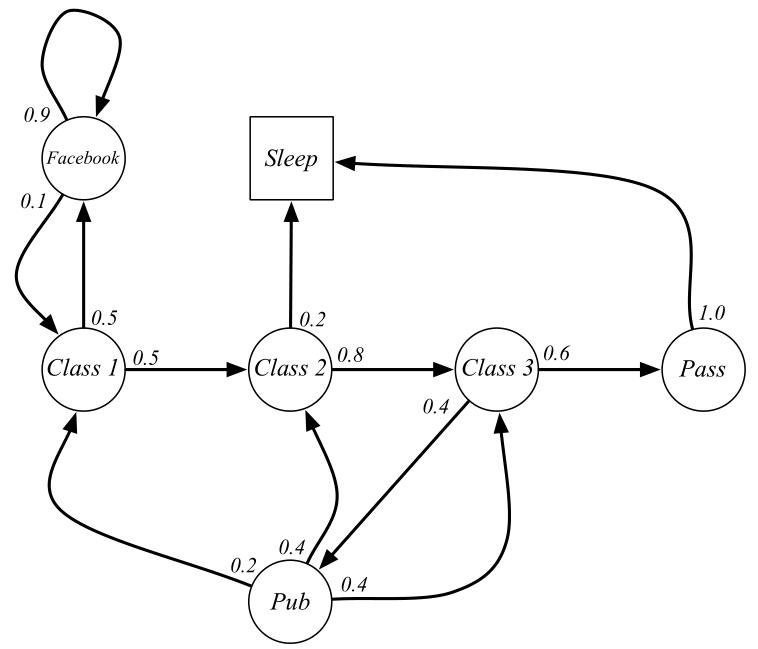
这个任务中有7个状态$(Facebook,Class1,Class2,Class3,Pass,Pub,Sleep)$。在每个状态对应着响应的转移概率，比如在$Class1$状态下，有0.5概率继续转移到$Class2$以及0.5的概率转移到$Facebook$，这里可以注意到每个状态转移概率之和为1。

在这里我们如果对这个马尔科夫过程，从$Class1$状态开始采样，将会得到很多幕（episode）的采样数据。其中每一幕序列可能为：

• C l a s s 1 , C l a s s 2 , C l a s s 3 , P a s s , S l e e p Class 1, Class 2, Class 3, Pass, Sleep C强化学习笔记：马尔可夫决策过程 Markov Decision Process(MDP)

  David Silver强化学习Lecture2：马尔可夫决策过程

  强化学习马尔可夫决策过程(MDP)基本原理

  强化学习：马尔可夫决策过程

  《基于逻辑马尔可夫决策过程的关系强化学习研究.nh》

  强化学习笔记-03有限马尔可夫决策过程MDP