算法备忘录——基础数据结构与复杂度

Posted 2022-12-08 zhou_chenz

基础数据结构与复杂度

数据的基本组织方式

连续存储结构——数组

特点： 

- 在连续的地址上存储某类型对象的元素。

优点：

- 可以通过索引随机快速地访问数组元素

缺点：

- 插入和删除元素操作不方便，随机插入/删除某元素，需要移动大量元素。

链式存储结构——链表

特点：

- 通过对象链接的方式，依次将某类型对象的元素通过链式结构链接起来。

优点：

- 可以很方便的插入/删除某元素，而不需要移动其它元素。

缺点：

- 不能通过索引值随机访问，访问元素需要从头开始，一个一个链接地查找。

2.背包、栈、队列实现方式对比

背包

- 定义： 某种类型对象元素的集合

- 基本API： 

 add() ——> 将元素加入bag

contains() ——> 判断元素是否属于bag

get() ——> 从bag中获取某元素值。

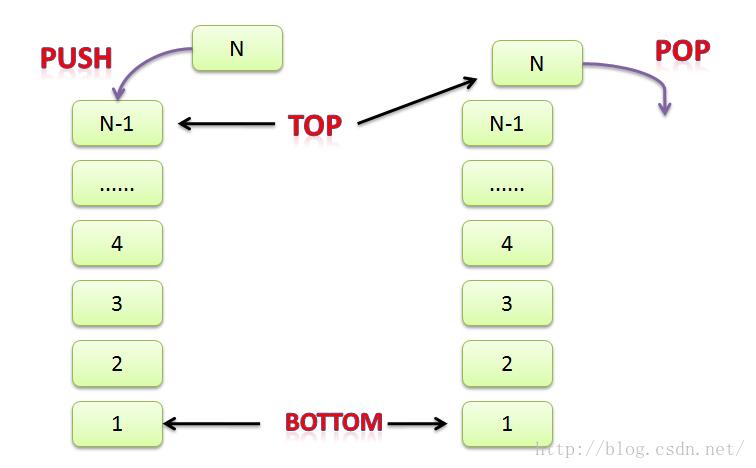
栈

- 定义 ：一种支持后入先出(LIFO) 顺序保存和访问某对象元素的结构

- 基本API： 

push() ——> 将元素加入statck

pop() ——> 将元素从stack的top删除

seek() ——> 获取stack 的 top元素值，但不删除元素。

队列

- 定义 ：一种支持先入先出(FIFO) 顺序保存和访问某对象元素的结构

- 基本API： 

enqueue() ——> 将元素加入到queue的tail

dequeue() ——> 将元素从queue的head取出并删除

seek() ——> 获取queue 的 head元素值，但不删除元素。

用数组与链表分别实现背包、栈、队列三种数据结构的方法对比

数组实现:

- 优点

* 背包实现中，若对元素进行排序，可以随机快速访问任意元素。

- 缺点

* 背包，堆栈，队列中，构造之初就得确定数组的大小，动态增加/减少数组的大小，需要耗费时间在重新开辟地址空间，并搬运元素上。

链表实现:

- 优 点

* 可以很方便地将元素插入/删除到对应的数据结构中，无需考虑动态增加/减少元素存储结构空间大小的问题。

   - 缺点

* 随机访问任意元素的速度较慢，平均时间复杂度是 N 以上。

3.时间复杂度与空间复杂度

时间复杂度

时间复杂度近似函数T(N) 表示趋近与 ~ 某个高阶多项式，忽略低阶项(和泰勒级数相反，泰勒忽略高阶项)

 一般 O(N)表示复杂度上界，Omiga(N)表示下界

复杂度等级：

T(N)近似函数 ~ 时间随数据大小N变化快慢函数——lg 函数表示以2为底的对数, 测试数据大小N一般是 2,、4、8、16、2^n 以2的幂增加，T(N)之后为典型代码

1      ——> i++

lg(N) ——> 二分查找

   N  ——> for(int i=0;  i < N; i++) a[i] = i;

Nlg(N) ——> 分治类算法(归并，快速排序)

N^2   ——> 

for(int i=0;  i < N; i++) 

for(int j=0;  i < N; i++) 

a[i][j] = j;

冒泡排序,选择排序

N^3 ——> 三层for循环

2^N ——> 穷举查找，检查所有子集。

……

空间复杂度

在算法运行过程中，所需额外交换空间大小，随着输入数据大小N的变化趋势。

4.实际应用中需要观察考虑的point

输入模型

输入数据对算法性能的影响，比如插入排序，输入数据原本的有序程度，直接影响的排序过程中需要比较和交换的次数，因而导致算法不稳定。

有序输入N和元素相比随机输入N和元素，插入排序时间复杂度从 N ~ N^2 级别的变化

内循环

算法执行过程中，最复杂耗时操作的代码段中，for while 等循环运算的嵌套个数，一般时间复杂度都是循环嵌套的幂级数。

内循环是抛开计算机性能和输入数据特性，判断算法本身耗时和复杂程度的最重要point。

成本瓶颈

考虑计算机实际的结构，某些情况下，虽然理论上访问运算次数最少，但是比如数组存储在I/O访问的磁盘上，

虽然数学理论上多次访问数组才是最优算法，但是由于磁盘是耗时访问，访问1次磁盘的时间，是访问RAM内存或者Cache

内存时间的100倍以上，因而在算法实现中，50-80次的RAM访问，反而比1次磁盘访问更加节约时间。