全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之softmax图像多分类

Posted 2022-12-08 寒小阳

课程作业原地址：CS231n Assignment 1
作业及整理：@林凡莉 && @Molly && @寒小阳
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/79138352

1. 任务

这次练习跟SVM练习类似。你将完成下面的任务：

• 通过矩阵运算为Softmax分类器实现一个损失函数
• 为这个损失函数的分析梯度实现一个完全矢量化的表达式
• 用数值梯度检查上面的分析梯度的值
• 使用验证集找到最好的学习率和正则化强度
• 用随机梯度下降法优化损失函数
• 可视化最终学习到的权重

2 知识点

2.1 Softmax分类器

Softmax分类器也叫多项Logistic回归（Multinomial Logistic Regression），它是二项Logistic回归在多分类问题上的推广。它和SVM构成了两类最常用的分类器。但跟SVM不同的是，Softmax分类器输出的结果是输入样本在不同类别上的概率值大小。我们用CS231n课件上的一张图来说明它们两者在计算上的区别：

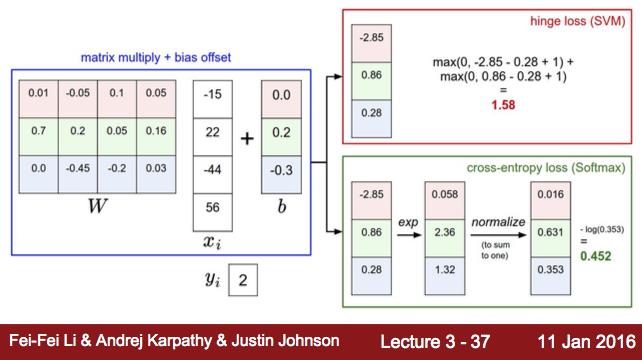
图中的$W$为权重矩阵，假设它的大小为K*D，那么K就是类别个数，D为图像像素值大小。$x_i$为图像向量，$b$为偏置向量。计算 $$Wx_i+b$$ 得到的新向量表示图片$x_i$在不同类别上的得分。上面的式子经常用

$$f(x_i,W)$$ 来表示，叫做得分函数（score function）。

而SVM和Softmax的一个区别在于，Softmax在得到分值向量之后还要对分值向量进行再处理，第一步是通过指数函数将分值向量映射得到新向量，第二步是对新向量进行归一化。最终得到的向量上的数值可以诠释为该图像为某类别的概率大小，而SVM得到的向量仅仅是图像在不同类别上的分值大小，没有概率的含义。
这个对分值向量处理的过程，可以用下面的函数来表示

$$p_k = \\frace^f_k \\sum_j e^f_j$$

k为某个特定的类别，f为分值向量，j为任意的类别，$p_k$表示k类别上的概率值大小。

2.2 Softmax分类器的损失函数

既然Softmax分类器得到的输出向量为每个类别的概率值大小，我们希望正确类别对应概率值（也就是概率的对数值）越大越好，那么也就是希望概率对数值的负数，越小越好。而这个概率对数值的负数也就是我们的损失函数。下图给出了损失函数的计算公式：

虽然课件上并没说明，但Softmax的这个损失函数还有一个非常fancy的名字：交叉熵损失函数（Cross Entroy Loss），它跟最大似然估计的思想很接近。为了不增加大家的学习负担，这里就不多解释了。^_^

以上是Softmax分类器对单个图像的损失函数定义，但在实际模型的训练过程中，我们会有很多的图像，所以我们会对所有图像的损失函数求均值得到一个数据损失（data loss）。然后，为了避免出现过拟合的问题，减少模型的复杂度，我们还在损失值里加了正则项，也叫正则损失（regularization loss）。这两个损失值加起来就是训练图像的损失值：

$$L = \\underbrace \\frac1N \\sum_i L_i _\\textdata loss + \\underbrace \\frac12 \\lambda \\sum_k\\sum_l W_k,l^2 _\\textregularization loss$$
式子中的1／2是为了在求梯度的过程中，减少一些计算量，因为 $W^2$会得到 $2W$,而1/2正好抵消了这里的2。

值得一提的是，在实际训练中，我们的训练集往往非常大，计算全部数据集上的损失值，然后再对其计算梯度的运算量非常大，训练速度也非常慢。所以我们经常使用随机梯度法（Stochastic Gradient Descent） 随机抽取训练集中的图像，对其进行损失值和梯度的计算来近似整个训练集的损失值和梯度。

2.3 数值梯度 vs. 解析梯度

计算梯度有两种方法：一种是缓慢的近似法（数值梯度法），实现相对简单。另一种方法（解析梯度法）计算迅速，结果精确，但实现时容易出错，且需要使用微分的知识。
数值梯度的思想就是把一个函数的定义域划分成等距的有限个数，然后通过下面的方程近似得到梯度值：

$$\\fracdf(x)dx = \\lim_h\\ \\to 0 \\fracf(x + h) - f(x)h$$
也就是说，当我们知道函数 $f(x)$，并且划分的等距离间隔h也确定下来的时候，那我们就可以根据上面的公式近似得到任何一个 $x$对应的梯度值（导数值）。

而解析梯度的意思是将我们的函数$f(x)$直接进行微分求导，比如将 $y=x^2$求导，得到的导数是 $x$。这看似简单，但是当我们的函数非常复杂的时候，求导可能也会遇到比较大的问难，实现起来比较不容易。

相比之下，用数值梯度法来近似计算梯度是比较简单，但问题在于它的结果最终也只是近似，尤其是当我们把h选得很大的时候，计算的梯度值就会非常不准确。而解析梯度法用微分分析直接得到梯度的公式，用公式计算梯度速度很快，但实现的时候容易出错。所以，实际操作时常常将解析梯度法的结果和数值梯度法的结果作比较，以此来检查其实现的正确性。

接下来，我们用课堂里的例子来具体地说明一下数值梯度是如何计算得到的：

梯度dW说白了就是损失函数L对W求导得到的导数值，但因为W本来含有多个变量，所以求导结果的并不是一个数值，而是一个向量，甚至是矩阵。而导数本身的含义就是当自变量变化一个单位的时候，因变量会跟随着变化多少。在我们的例子里，梯度向量dW中的每一个值代表的是当该值对应的权重变量变化0.0001的时候，损失函数值会变化多少。具体的计算过程可以参照上图。因为对于W中的每一个权值变量都要重新计算一次损失函数值，可想而知当W中又很多变量的时候，运算量是很大的。

那解析梯度又如何计算呢？如何直接求得损失函数对W中各个变量的导数呢？这里需要用到的核心技巧就是下面的这个chain rule：
$$\\frac\\partial f \\partial s = \\frac\\partial f \\partial p \\frac\\partial p \\partial s$$

在运用这个chain rule之前，先让我们回忆下前面提到过的各个函数的数学表达式：
下面的是我们的分值函数：

$$f_i = Wx_i+b$$
而我们知道，在softmax里，分值需要转化成概率值，损失函数的值就是正确类别的分值所对应的负对数，下面列出公式：
pk=e全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之SVM图像分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之特征抽取与图像分类提升

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之softmax图像多分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之神经网络细解与优化尝试

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之双层神经网络完成图像多分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之基于cifar10的卷积神经网络实践