树的操作

Posted 2022-12-07 勇士后卫头盔哥

树的查找

在之前树的定义中我们可以知道,我们提供的查找操作有基于数据元素值的查找和基于结点的查找,树是一种非线性结构,当我们查找根据数据元素值查找时需要用到递归调用,从根节点出发自顶向下对子节点进行查找,所以必须提供一个开始查找的结点,对于树中数据元素和结点的查找如下
基于数据元素值的查找

代码:

GTreeNode<T> *find(GTreeNode<T>* node,const T& value)const

	GTreeNode<T> *ret = NULL;
	if(node!=NULL)
	
	     if(node->value == value)//递归出口,找到则返回
	     
	        return node;
	     
	     else
	     
	         for(node->child.move(0);!node->child.end()&&(ret==NULL);node->child.next())//递归调用,在根节点的子节点链表中查找
	         
	             ret = find(node->child.current(),value);
	         
	     
   
   return ret;

基于结点的查找

代码:

GTreeNode<T> *find(GTreeNode<T>* node,GTreeNode<T>* obj)const

     GTreeNode<T> *ret = NULL;
     if(node==obj)//递归出口
     
         return node;
     
     else
     
         if(node!=NULL)
         
             for(node->child.move(0);!node->child.end()&&(ret==NULL);node->child.next())//递归调用,在根节点的子节点链表中查找
             
                 ret = find(node->child.current(),obj);
             
         

     
     return ret;

插入操作

对于插入操作有插入新结点和插入新元素两种操作,树是非线性的,无法采用下标的形式定位数据元素,每一个树结点都有唯一的前驱结点(父节点),因此,必须先找到前驱结点才能完成新结点的插入
对于插入新结点的流程图如下所示

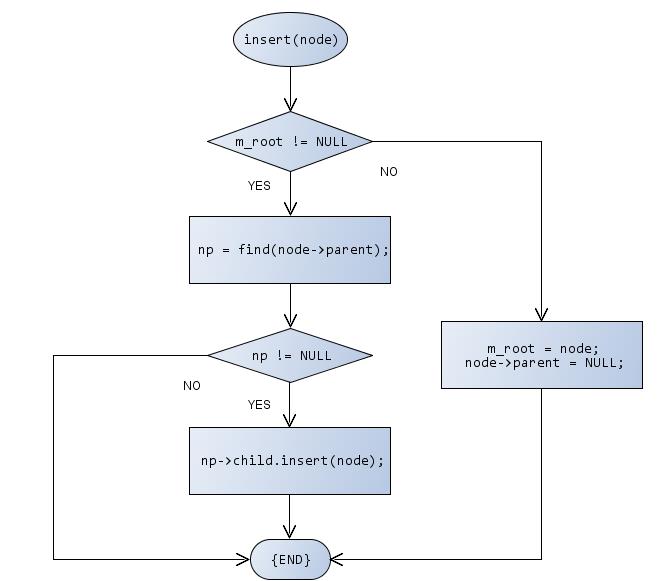
代码:

bool insert(TreeNode<T>* node)

   bool  ret = true;
   if(node != NULL)
   
       if(this->m_root == NULL)//判断插入的结点是否为根结点,如果是的则设置为根节点
       
            this->m_root = node;
            node->parent = NULL;
       
       else//插入操作
       
           GTreeNode<T>* np = find(node->parent);//找到插入结点的父节点
           if(np!=NULL)
           
               GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);
               if(np->child.find(n)<0)//判断父节点的子节点链表中是否已经存在该结点
               
                   np->child.instert(n);//不存在则插入到父节点的子节点链表中
               

           
       
   
  else
  
       THROW_EXCEPTION(InvalidOperationException,"Invaild parent tree node.....");
  
   return ret;

对于插入数据元素的流程图如下所示
插入数据元素的时候我们需要指定这个元素的父节点,并创建一个新节点出来,指定这个新节点的父节点及其value,最后调用插入新结点的函数即可

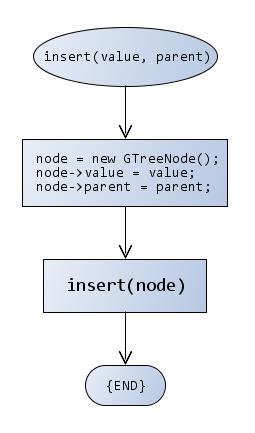
bool insert(const T& value,TreeNode<T>* parent)

    bool  ret = true;
    /*构造插入结点*/
    GTreeNode<T>* node = new GTreeNode<T>();
    if(node!=NULL)
    
          node->value = value;
          node->parent = parent;
          insert(node);//调用重载插入结点函数
    
    else
    
        THROW_EXCEPTION(NoEnougMemoryException,"no memery to using");
    
    return ret;

实战演练

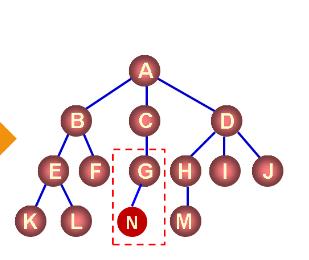
int main()

  GTree<char> t;
  GTreeNode<char> *node = NULL;

  t.insert('A',NULL);
  node = t.find('A');
  t.insert('B',node);
  t.insert('C',node);
  t.insert('D',node);

  node = t.find('B');
  t.insert('E',node);
  t.insert('F',node);

  node = t.find('E');
  t.insert('K',node);
  t.insert('L',node);

  node = t.find('C');
  t.insert('G',node);

  node = t.find('D');
  t.insert('H',node);
  t.insert('I',node);
  t.insert('J',node);


  node = t.find('H');
  t.insert('M',node);
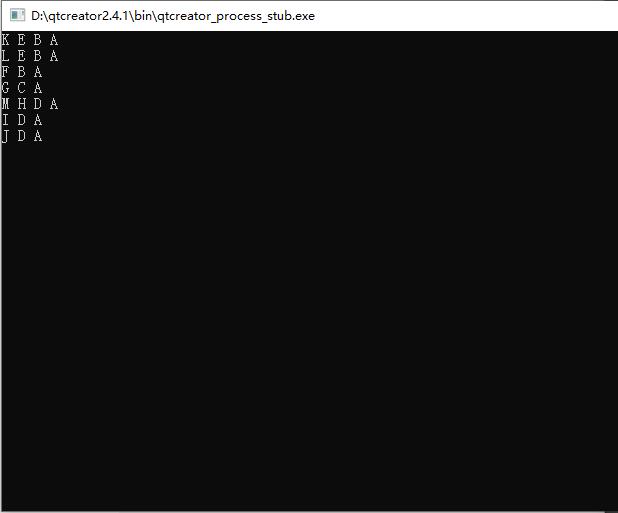
  char*s = "KLFGMIJ";
  for(int i=0;i<7;i++)
  
      TreeNode<char>* node = t.find(s[i]);
      while(node!=NULL)
      
          cout<<node->value<<" ";
          node = node->parent;
      
      cout<<endl;
  
  return 1;