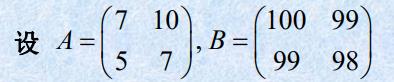《数值分析》-- 向量和矩阵的范数Ax=b的误差分析
Posted 胜天半月子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数值分析》-- 向量和矩阵的范数Ax=b的误差分析相关的知识,希望对你有一定的参考价值。
文章目录
一、向量和矩阵的范数
范数用来度量向量和矩阵的大小。
1.1 向量的范数
- 定义

- 常用范数
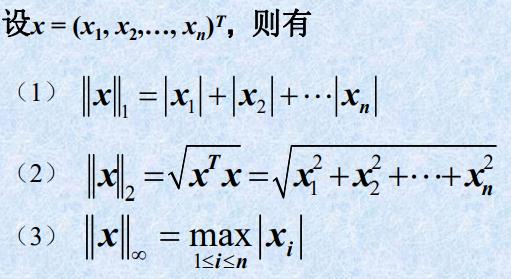
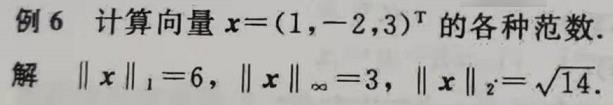
1.2 矩阵的范数
- 定义

- 定理


二、误差分析
- 数据扰动
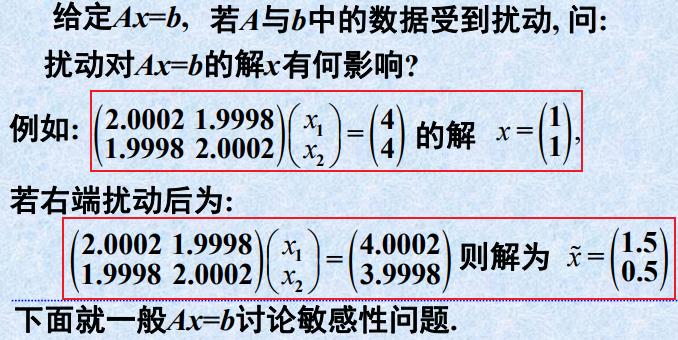

δ x = A − 1 δ b = > ∣ ∣ δ x ∣ ∣ < ∣ ∣ A − 1 ∣ ∣ ⋅ ∣ ∣ δ b ∣ ∣ \\delta x = A^-1 \\delta b => ||\\delta x|| < || A^-1|| · ||\\delta b|| δx=A−1δb=>∣∣δx∣∣<∣∣A−1∣∣⋅∣∣δb∣∣
∣ ∣ b ∣ ∣ = ∣ ∣ A x ∣ ∣ ||b|| = ||Ax|| ∣∣b∣∣=∣∣Ax∣∣ ≤ \\le ≤ ∣ ∣ A − 1 ∣ ∣ ⋅ ∣ ∣ x ∣ ∣ = > || A^-1|| · ||x|| => ∣∣A−1∣∣⋅∣∣x∣∣=> 1 ∣ ∣ x ∣ ∣ \\frac 1||x|| ∣∣x∣∣1 ≤ \\le ≤ ∣ ∣ A ∣ ∣ ∣ ∣ b ∣ ∣ \\frac ||A||||b|| ∣∣b∣∣∣∣A∣∣
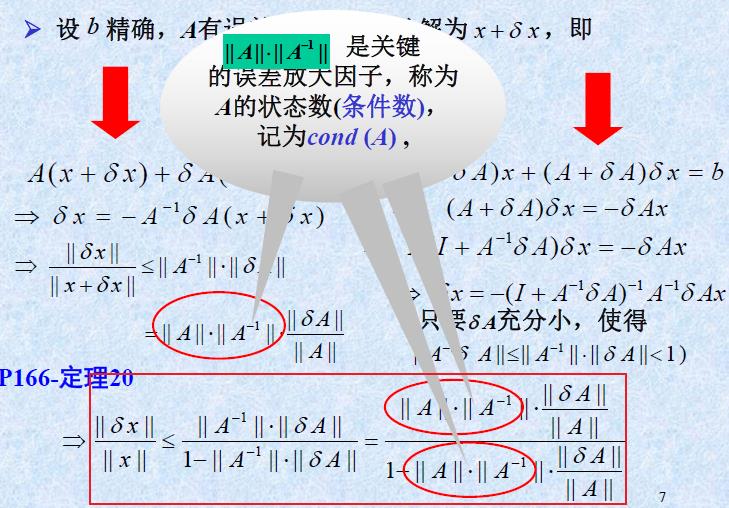



总结
- 理论

以上是关于《数值分析》-- 向量和矩阵的范数Ax=b的误差分析的主要内容,如果未能解决你的问题,请参考以下文章