谱聚类（spectral clustering)及其实现详解

Posted 2022-12-06 杨铖

Preface
开了很多题，手稿都是写好一直思考如何放到CSDN上来，一方面由于公司技术隐私，一方面由于面向对象不同，要大改，所以一直没贴出完整，希望日后可以把开的题都补充全。

---

先把大纲列出来：

一、从狄多公主圈地传说说起
二、谱聚类的演算
  （一）、演算
      1、谱聚类的概览
      2、谱聚类构图
      3、谱聚类切图
        （1）、RatioCut
        （2）、Ncut
        （3）、一点题外话
  （二）、pseudo-code
三、谱聚类的实现(scala)
  （一）、Similarity Matrix
  （二）、kNN/mutual kNN
  （三）、Laplacian Matrix
  （四）、Normalized
  （五）、Eigenvector(Jacobi methond)
  （六）、kmeans/GMM
四、一些参考文献

---

一、从狄多公主圈地传说说起

       谱聚类（spectral clustering）的思想最早可以追溯到一个古老的希腊传说，话说当时有一个公主，由于其父王去世后，长兄上位，想独揽大权，便杀害了她的丈夫，而为逃命，公主来到了一个部落，想与当地的酋长买一块地，于是将身上的金银财宝与酋长换了一块牛皮，且与酋长约定只要这块牛皮所占之地即可。聪明的酋长觉得这买卖可行，于是乎便答应了。殊不知，公主把牛皮撕成一条条，沿着海岸线，足足围出了一个城市。
       故事到这里就结束了，但是我们要说的才刚刚开始，狄多公主圈地传说，是目前知道的最早涉及Isoperimetric problem（等周长问题）的，具体为如何在给定长度的线条下围出一个最大的面积，也可理解为，在给定面积下如何使用更短的线条，而这，也正是谱图聚类想法的端倪，如何在给定一张图，拿出“更短”的边来将其“更好”地切分。而这个“更短”的边，正是对应了spectral clustering中的极小化问题，“更好”地切分，则是对应了spectral clustering中的簇聚类效果。
       谱聚类最早于1973年被提出，当时Donath 和 Hoffman第一次提出利用特征向量来解决谱聚类中的f向量选取问题，而同年，Fieder发现利用倒数第二小的特征向量，显然更加符合f向量的选取，同比之下，Fieder当时发表的东西更受大家认可，因为其很好地解决了谱聚类极小化问题里的NP-hard问题，这是不可估量的成就，虽然后来有研究发现，这种方法带来的误差，也是无法估量的，下图是Fielder老爷子，于去年15年离世，缅怀。

二、谱聚类的演算

（一）、演算

1、谱聚类概览

       谱聚类演化于图论，后由于其表现出优秀的性能被广泛应用于聚类中，对比其他无监督聚类（如kmeans），spectral clustering的优点主要有以下：

1.过程对数据结构并没有太多的假设要求，如kmeans则要求数据为凸集。
2.可以通过构造稀疏similarity graph，使得对于更大的数据集表现出明显优于其他算法的计算速度。
3.由于spectral clustering是对图切割处理，不会存在像kmesns聚类时将离散的小簇聚合在一起的情况。
4.无需像GMM一样对数据的概率分布做假设。

       同样，spectral clustering也有自己的缺点，主要存在于构图步骤，有如下：

1.对于选择不同的similarity graph比较敏感（如 epsilon-neighborhood， k-nearest neighborhood，fully connected等）。
2.对于参数的选择也比较敏感（如 epsilon-neighborhood的epsilon，k-nearest neighborhood的k，fully connected的 ）。

       谱聚类过程主要有两步，第一步是构图，将采样点数据构造成一张网图，表示为G(V,E)，V表示图中的点，E表示点与点之间的边，如下图：
              
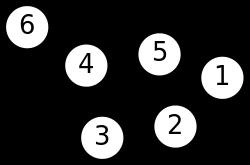
                            图1 谱聚类构图(来源wiki)
       第二步是切图，即将第一步构造出来的按照一定的切边准则，切分成不同的图，而不同的子图，即我们对应的聚类结果，举例如下：
              
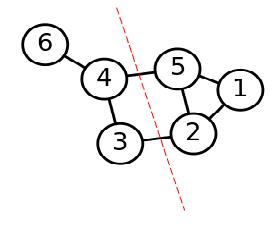
                            图2 谱聚类切图
       初看似乎并不难，但是…，下面详细说明推导。

2、谱聚类构图

       在构图中，一般有三种构图方式：
       1. $\\varepsilon$-neighborhood
       2. k-nearest neighborhood
       3. fully connected
       前两种可以构造出稀疏矩阵，适合大样本的项目，第三种则相反，在大样本中其迭代速度会受到影响制约，在讲解三种构图方式前，需要引入similarity function，即计算两个样本点的距离，一般用欧氏距离：$s_i,j = \\left \\| x_i-x_j \\right \\| ^2$, $s_i,j$表示样本点$x_i$与$x_j$的距离，或者使用高斯距离$s_i,j=e^\\frac-\\left \\| x_i-x_j \\right \\|^22\\sigma ^2$，其中$\\sigma$ 的选取也是对结果有一定影响，其表示为数据分布的分散程度，通过上述两种方式之一即可初步构造矩阵$S:S_i,j=[s]_i,j$，一般称 为Similarity matrix(相似矩阵)。
       对于第一种构图$\\varepsilon$ -neighborhood，顾名思义是取$s_i,j\\leq \\varepsilon$的点，则相似矩阵$S$可以进一步重构为邻接矩阵(adjacency matrix)$W$ :

$$W_i,j=\\left\\\\beginmatrix 0,\\quad if \\quad s_i,j>\\varepsilon\\\\ \\varepsilon,\\quad if \\quad s_i,j\\leq \\varepsilon \\endmatrix\\right.$$
       可以看出，在 $\\varepsilon$-neighborhood重构下，样本点之间的权重没有包含更多的信息了。
       对于第二种构图k-nearest neighborhood，其利用KNN算法，遍历所有的样本点，取每个样本最近的k个点作为近邻，但是这种方法会造成重构之后的邻接矩阵 $W$非对称，为克服这种问题，一般采取下面两种方法之一：
       一是只要点$x_i$在 $x_j$的K个近邻中或者 $x_j$在 $x_i$的K个近邻中，则保留 $s_i,j$，并对其做进一步处理 $W$，此时 为：
Wi,j=Wj,i=⎧⎩⎨0,ifxi∉KNN(Xj)andxj∉KNN(Xi)e谱聚类（spectral clustering）原理总结

谱聚类算法及其代码（Spectral Clustering）

Spectral clustering（谱聚类）算法的实现

Spectral clustering（谱聚类）算法的实现

Spectral clustering（谱聚类）算法的实现

谱聚类算法(Spectral Clustering)优化与扩展（转载）