全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之双层神经网络完成图像多分类

Posted 2022-12-06 寒小阳

课程作业原地址：CS231n Assignment 1
作业及整理：@林凡莉 && @Molly && @寒小阳
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/79139395

1 任务

在这个练习里，我们将实现一个完全连接的神经网络分类器，然后用CIFAR-10数据集进行测试。

2 知识点

2.1 神经元

要讲神经网络就得先从神经元开始说起，神经元是神经网络的基本单位，它的结构如下图所示：

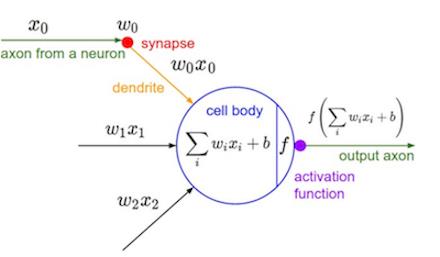
神经元不管它的名字有多逼格，它本质上不过是一个函数。就像每个函数都有输入和输出一样，神经元的输入是一个向量，里面包含了很多个$x_i$（图左边），输出的是一个值（图右边）。神经元在这个过程中只做了两件事：一是对输入向量做一次仿射变换（线性变化+平移, scaling+shift），用公式表示就是

$$\\sum_iw_ix_i +b$$ 二是对仿射变换的结果做一次非线性变换，即 $$f(\\sum_iw_ix_i +b)$$ 这里的f就叫做激活函数。权值 $w_i$和偏置项 $b$是神经元特有的属性，事实上，不同神经元之间的差别主要就三点：权重值，偏置项，激活函数。总的来说，神经元的工作就是把所有的输入项$x_i$与其对应的权值相乘求和，然后加上偏置项 $b$，之后通过一个激活函数求得最终的值，即这个神经元的输出。

激活函数有很多种，下面介绍一个叫sigmoid的激活函数： $$\\sigma(x) = 1/(1+e^-x)$$
这个函数很有意思，它把任何一个属于值域R的实数转换成0到1之间的数，这使得概率的诠释变得可能。但是在训练神经网络的时候，它有两个问题，一是当输入的仿射变换值太大或者太小的时候，那f关于x的梯度值就为0，这不利于后面提到的反向传播算法中梯度的计算。第二个问题在于它的值不是中心对称的，这也导致梯度更新过程中的不稳定。Sigmoid的函数图像大概长下面这样：

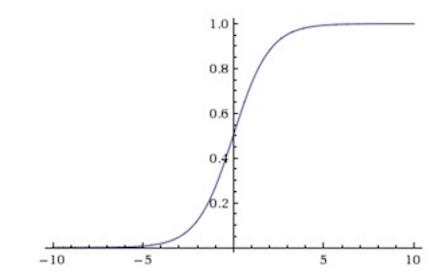
如果现在我们把实数1也放进输入的向量中得到$\\vecx$，把偏置项放进权值向量中得到$\\vecw$，那么包含sigmoid激活函数神经元的工作就可以简洁地表示为：

$$y=sigmoid(\\vecw^T\\centerdot\\vecx)$$
聪明的你或许已经看出来：既然sigmoid函数的输出可以诠释为在0到1间的概率值大小，那么，单个神经元其实就可以当作一个二类线性分类器来使用。也就是说，假设我们输入的是一个图像向量，将它乘以权重向量之后再通过sigmoid函数，如果得到的值如果大于0.5，那这幅图片就属于这个类别，否则就不是。

实践中比较常用的是这个叫ReLU的激活函数：

$$f(x) = \\max(0, x)$$
这个函数把输入的x与0做比较，取两者中更大的那个作为函数的输出值。它的图像表示如下：

ReLu在实践中被证明的优点是它在随机梯度下降法中收敛效果非常好，此外它的梯度值非常简单。但它的缺点也非常明显，就是当它的梯度为0的时候，这个神经元就相当于把从后面传过来的梯度值都变成了0，使得某些变量在梯度下降法法中不再变化。cs231n官网笔记里有关于不同激活函数的详细介绍，大家有兴趣可以看一下： http://cs231n.github.io/neural-networks-1/。

2.2 神经网络

当我们把很多个神经元按照一定规则排列和连接起来，便得到了一个神经网络。如果网络中每层之间的神经元是两两连接的，这样的神经网络就叫做全连接神经网络（Fully-connected Neural Network）。下图展示了两个不同层数的全连接神经网络：

图中的神经网络包含一个输入层（Input Layer）和输出层（Output Layer），中间的层叫隐藏层（Hidden Layer）。需要注意的是，输入层包含的并不是神经元，而是输入向量$\\vecx$，上图输入层中圆圈的表示方法其实有些误导。输出层在最后起的作用相当于一个多类分类器，实践中经常采用Softmax分类器。而中间的隐藏层，无论有多少层，隐藏层们在一起做的事情相当于输入向量特征的提取。

现在我们从计算的角度来分析下一层神经网络到底在做什么。我们知道一个神经元做的事情是把一个向量变成一个标量，那当我们把很多个神经元排列起来变成一个神经网络层的时候，这个层输出的结果应该是跟层里神经元数目相当的很多个标量，把这些标量排列起来就成了向量。也就是说，一个神经网络层做的事情是把一个向量变成了另一个向量，这中间的计算过程无非就是矩阵运算再加一个激活函数。假设输入向量为$\\vecx$，矩阵和向量的乘法运算可以表示为$W\\vecx$，这里的矩阵$W$是将层中的每一个神经元的转置权重向量$\\vecw_i^T$由上到下排列得到,就像这样：

$$W=\\beginbmatrix \\vecw^T_1 \\\\ \\vecw^T_2 \\\\ \\vecw^T_3 \\\\ \\vecw^T_4 \\\\ \\endbmatrix$$
现在我们拿一个简单的例子来感受一下一个神经网络层在做的事情（图片来源于台湾李宏毅教授深度学习的课件）：

图中的网络一共有四层，两个隐藏层，一个输入层和一个输出层，每个隐藏层中又包含两个神经元。假设输入为向量$\\beginbmatrix1\\\\-1\\endbmatrix$, 将隐藏层中每个神经元的权重都作为一行，那么第一个隐藏层的权重矩阵就是一个大小为2x2的矩阵（如图中黄色字体显示），权重矩阵与输入向量相乘再加上偏置向量得到的向量$\\beginbmatrix4\\\\-2\\endbmatrix$是每个神经元对输入向量做仿射变换的结果，之后通过激活函数$\\sigma$得到第一个隐藏层的输出 [0.980.12全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之SVM图像分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之特征抽取与图像分类提升

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之softmax图像多分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之神经网络细解与优化尝试

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之双层神经网络完成图像多分类

全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之基于cifar10的卷积神经网络实践