FXcX KMP Search Algorithm

Posted 2022-12-06 xioacd99

更好的阅读体验与反馈请点击下面的网址（这是我在语雀上的博客）
https://www.yuque.com/u12549703/xql1va/ny150b

（不想做笔记的也推荐去上面那个，排版和阅读体验式真的好）

概要：本文将会从KMP算法产生的动机入手，讲解KMP算法原理的两种理解思路。之后，我们会先针对代码实现（本文选用的是C++）中出现的一些问题进行讲解，最后给出下标从0开始和下标从1开始的两种版本的代码实现。

Are u Ready？
接下来让我们抽丝剥茧地认识KMP的本质，并解决实现上的理解问题。
本文保证绝不会像大佬讲题，“你看，画一条辅助线，对不对，答案出来了”，“显而易见选C”……

KMP算法产生的动机

我们知道，对于Brute Force算法，当主串和子串发生不匹配时，主串会进行回溯，而这严重影响效率。

int bruteForce_search(string& s, string t, int pos) 
    int i = pos, j = 0;
	int slen = s.size(), tlen = t.size();

    while (i < slen && j < tlen) 
        if (s[i] == t[j]) 
            ++i, ++j;
         else 
            i = i - j + 2;  // 发生不匹配,主串回溯到很远之前
            j = 0;
        


    if (j >= tlen) 
        return j - tlen;
     else 
        return -1;
    

最好情况下，每次不成功的匹配都发生在模式串的第一个字符，设主串的长度为n，子串的长度为m，则最好的情况下匹配成功的平均比较次数为（O(n+m)）

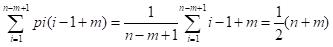
最坏情况下，每趟不成功的匹配都发生在模式串的最后一个字符与主串中相应字符的比较O(n*m)

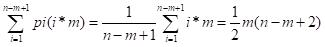
于是KMP就想：我能不能不让主串回溯，就看主串下一步需要和子串的哪一个进行比较，然后继续比不就可以了吗？这就是KMP算法的主要思想，最后得到的KMP算法有O(n+m)的最坏时间复杂度

从0开始的

int kmp_search(string& s, string& t, int pos) 
    vector<int> next(ikmp_table(t));

    int i = pos, j = 0;
    int slen = s.size(), tlen = t.size();
    while (i < slen && j < tlen) 
        if (j == -1 || s[i] == t[j]) 
            ++i, ++j;
         else 
            j = next[j];
        
    

    if (j >= tlen) 
        return i - tlen;
     else 
        return -1;
    

从1开始的（这里仅给出不同的部分）

    int i = pos, j = 1;
    while (i <= slen && j <= tlen) 
        if (j == 0 || s[i] == t[j]) 
    

附：虽然BF算法的最坏时间复杂度是O（n*m），但在一般情况下，其实际执行的实际近似为O（n+m），所以现在大家仍然在广泛地使用BF算法（理解起来简单）KMP算法仅当模式串和主串直接存在许多“部分匹配”的情况下才显得比BF算法快得多。但是KMP算法的最大特点是指示主串的指针不需要回溯，整个匹配过程中，对主串仅需从头到尾扫描一遍，这对处理从外设输入的庞大文件很有效，可以边读边输入匹配，而无需从头再读。

KMP算法理解的两种思路

在介绍KMP算法的原理之前，我们先来了解一个小的背景知识。

KMP算法是Jamel H.Morris首先发现的，然后Donald Knuth在很短的时间里，又从对自动机状态的研究里发现了这个排序算法（两个人是独立发现的）。为什么又是3个人呢？1970年，Morris和Pratt一起发表了技术报告。（可能他们当时不知道Knuth也发现了，但后来1977年大家一起publish这个算法）（另外，在1969年，Matiyasevich发现了一个类似的算法，这里就不再多说了）

介绍这个背景主要在说明既然三大头都能从不同的研究领域发现这个算法，那么我们也可以从不同的角度来理解这个算法。这里我们给出两种算法理解的思路。（讲解如何计算next数组的值）（因为书上都是用1作为起始索引，为了大家的方便，本文在讲解时同样以1作为起始索引。在实现时分别给出从0和从1开始的版本）

首先我们给出一个非常简单的例子“abaa”，我们可以轻而易举地知道它的next数组的值分别为[0, 1, 0, 2]

1. 最长公共子串法

   对于一个子串，当我们正在比较tj时，这时tj的next的值是下面这样计算
   构造字符串“t1 … tk-1”，它满足和“tj-k+1 tj-k+2 … tj-1”相等。而且这是能构造的符合要求的最长字符串。next的值就是它们的长度+1。（+1是因为你比较的是下一个）直白一点就是，你拿着笔一边从左往右画，一遍从右往左画（从右往左画，但读的时候还是从左往右读；而且记住是从当前的前一个开始画），划线的两个字符串达到最大相等。

   如上面的“abaa”，当我们在比较第3个a的时候
   左->右：“a”
   右->左：“a”
   相等，那继续

   左->右：“ab”
   右->左：“ba”
   不等，结束，返回最大长度+1，即1 + 1 = 2

2. 前缀后缀法

   这种方法计算tj的next值的时候，要构造一个字符串“t1 t2 … tj”来看前缀和后缀共有元素的最长长度maxlen，最后的next值 = j - 1（已匹配的字符数目） - maxlen（这个用来理解思想（两种的本质都一样）可能很好，但无论是用来手算还是实现代码都特别难，效率也不好提升）

   同样以上面的第3个a为例，此时构造的字符串为“abaa”
   前缀集合为[a, ab, aba]（就是不要最后一个），后缀集合为[baa, aa, a]（就是不要第一个）可以简记为“前缀不要后面，后缀不要前面”

   我们可以看到，共有元素为‘a’，长度为1。现在已经匹配了3个，那么next的值就是 3 – 1 = 2。

   特别地，对于单元素‘a’，它的前缀集合和后缀集合都是0

KMP算法实现

接下来我们来谈一谈next数组算法的实现

一般情况下，从1开始都是考试要求；从0开始都是实际实现要求。我们这里讲解从0开始的，从1开始的只需要在原代码上进行一些改动就可以了。

根据上面的推导我们可以知道，当next[j] = -1时，这时候主串和子串在第一个就不相等，即s[i] != t[0]，这时候我们应该移动主串至下一个位置与t[0]进行比较。而且我们知道，一旦j到了这个地方，那么就一定会产生这种操作，所以将j的值赋给next[i]。体现为代码就是

if (j == -1) 
	++i, ++j;
	next[i] = j;

而在当前元素比较相同的时候，我们自然能够想到要继续比较下一个，即++i, ++j。但是是否应该把j赋值给next[i]呢？这怎样和前面我们说的两种理解方法相对应呢？

我们之前说的两种理解方法都是从两个方向来看的。在具体的实现层面，如果我们继续用两个方向的思想，很显然写出的代码效率会很低。那么我们自然就想：能不能就同一个方向来实现呢？结果是肯定的。那又如何来实现呢？

这里就用到了一个处理手法，我们在进行搜索的时候。先来一个search之前的开胃菜—对t单独进行next数组值的求解。求解中我们既把t当成是主串串，也把t当做是模式串。但是我们通过两个指针的位置/速度差异来实现这种地位的不同。

也许你会问了，这又什么用呢？其实这种思想是我们上面提到的第一种理解的体现。我们这样采取了位置差异的指针，在任何一个有效的时刻，构建的字符串就是“t0 t1 … ti-1”和“t0 t1 … tj-1”，而且由于我们是从第一个逐渐开始构造的，所以我们在计算的时候可以充分利用j的值（这有点类似于动态规划的“记忆化”思想）。因此我们能够通过这种方式来得到next数组的值

体现为代码就是下面这种

vector<int> kmp_table(string& t) 
    int i = 0, j = -1;
    int len = t.size();
    vector<int> next(len, 0);
    next[0] = -1;

    // 因为现在比较的是t[i+1]
    while (i < len - 1) 
        if (j == -1 || t[i] == t[j]) 
            ++i, ++j;
            next[i] = j;
         else 
            j = next[j];
        
    

    return next;

如果你有一点好奇的话，那么你会发现，当t = “abcdab”这种情况时，上面的这个kmp_table()求得的结果和我们用定义求得的结果是不一样的。为什么会出现这种情况呢？因为t中出现了重复的子串“ab”，而原始的kmp_table()并未将其纳入考虑之中。更深入一点，原始的kmp_table()为了让大家理解起来简单一点，对“记忆化”思想的体现进行了一定程度的简化，实际上的情况应该是这样的

附：没有进行优化的kmp_table，在模式串自身没有重复子串的情况下有可能得到正确答案，否则多半会得到错误答案。但是对于最初的理解比较友好

    while (i < len - 1) 
        if (j == -1 || t[i] == t[j]) 
            ++i, ++j;
            if (t[i] != t[j]) 
                next[i] = j;
             else 
                next[i] = next[j];
            
         else 
            j = next[j];
        
    

这里其实存在着一个遗憾—对于上面的代码实现，本文只能给出两种说明：一是数学化的证明（我相信大家对于math wall都有畏惧感，所以这并不是一个好的说明方法）；二是“记忆化”思想的理解（虽然很直白，但还是存在着能理解的人觉得nice，不能理解的人？？？的情况）

优化后的kmp_table

vector<int> ikmp_table(string& t) 
    int i = 0, j = -1;
    int len = t.size();
    vector<int> next(len, 0);
    next[0] = -1;

    // 因为比较的是t[i+1]
    while (i < len - 1) 
        if (j == -1 || t[i] == t[j]) 
            ++i, ++j;
            if (t[i] != t[j]) 
                next[i] = j;
             else 
                next[i] = next[j];
            
         else 
            j = next[j];
        
    

    return next;

下面我们给出下标从1开始的需要改动的地方

没有优化的kmp_table

    int i = 1, j = 0;
    vector<int> next(len + 1, 0);
    next[1] = 0;

    while (i < len) 
        if (j == 0 || t[i] == t[j]) 

优化了的kmp_table

    int i = 1, j = 0;
    vector<int> next(len + 1, 0);
    next[1] = 0;

    while (i < len) 
        if (j == 0 || t[i] == t[j]) 

因为文章的篇幅比较长，所以希望大家对应没看懂的地方能多看几遍。同时，欢迎大家指出本文在理解上的不足和其他缺陷。