递归解决八皇后问题(Java)
Posted yuwenS.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了递归解决八皇后问题(Java)相关的知识,希望对你有一定的参考价值。
通过递归解决八皇后问题(Java)
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848 年提出:在 8×8 格的国际象棋上摆放八个皇后,使其不能互相攻击,即:任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?
解决思路
- 第一个皇后先放第一行第一列
- 第二个皇后放在第二行第一列、然后判断是否 可以, 如果不可以,继续放在第二列、第三列、依次把所有列都放完,找到一个合适位置
- 继续第三个皇后,还是第一列、第二列……直到第 8 个皇后也能放在一个不冲突的位置,算是找到了一个正确解
- 当得到一个正确解时,就会开始回溯,即将第一个皇后,放到第一列的所有正确解,全部得到
- 然后回头继续第一个皇后放第二列,后面继续循环执行 2,3,4 的步骤知道把第一个皇后放到第八列并查找到所有正确解
具体代码实现
public class Queue8
//定义max表示共有多少个皇后
int max = 8;
//定义数组array,保存皇后放置位置的结果,下标代表行,下标对应的值代表当前行的第几列
int[] array = new int[max];
//计数
int count = 0;
//放置第n个皇后
public void check(int n)
if (n == max)
print();
return;
//依次放入皇后,判读是否冲突
for (int i = 0; i < max; i++)
//先把当前这个皇后n,放到该行的第一列
array[n] = i;
//判断放置第n个皇后到n列时,是否冲突
if (judge(n))//不冲突
//接着放第n+1个皇后,开始递归
check(n + 1);
//如果冲突,继续执行,因为这个时候说明第一列的皇后所有正确解已经被找出可以进行下一列的皇后的摆放
//查看当我们摆放第n个皇后时,就去检测该皇后是否会和已经摆放的皇后冲突
public boolean judge(int n)
for (int i = 0; i < n; i++)
//1. array[i] == array[n] 表示判断 第 n 个皇后是否和前面的 n-1 个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第 n 个皇后是否和第 i 皇后是否在同一斜线
//3. 判断是否在同一行, 没有必要,n 每次都在递增
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i]))
return false;
return true;
//将可以将皇后摆放的位置输出
public void print()
count++;
for (int i : array)
System.out.print(i +" ");
System.out.println();
测试
测试代码
public static void main(String[] args)
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.println("共有 "+queue8.count+" 种解法");
测试结果
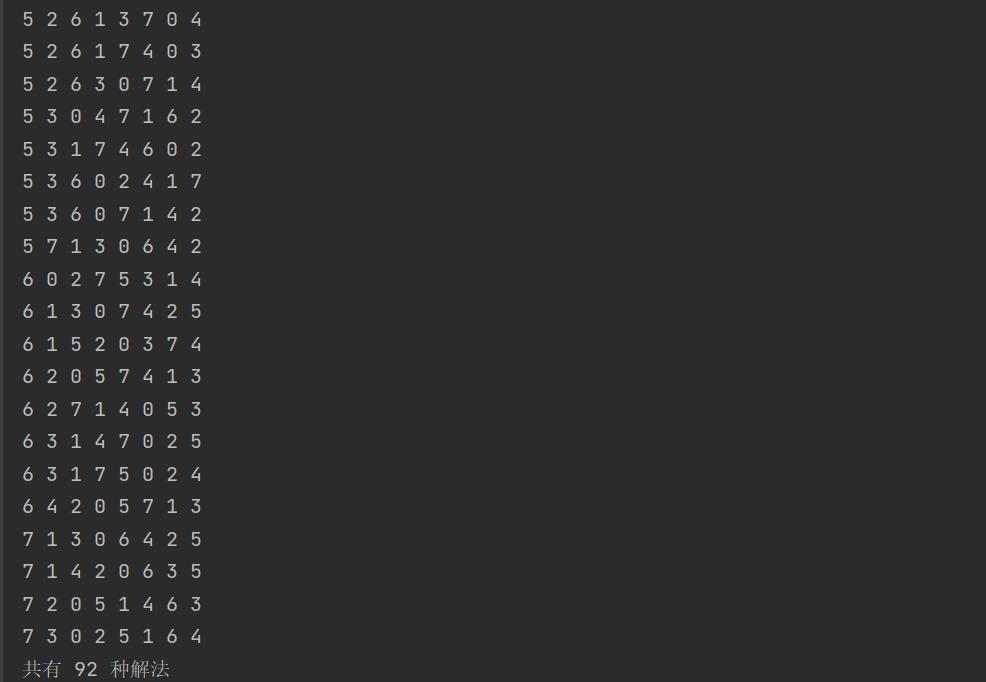
结果可以看出八皇后问题共有92种摆法
以上是关于递归解决八皇后问题(Java)的主要内容,如果未能解决你的问题,请参考以下文章