动态规划-第一节2：动态规划之使用“斐波那契数列”问题说明重叠子问题如何解决

Posted 2022-12-04 我擦我擦

• 注意：本文参考labuladong公众号总结
• 链接

文章目录

• • （1）暴力递归
  • （2）带有表的递归解法
  • （3）动态规划解法
  • （4）补充：关于斐波那契数列的极致解法（时间和空间均最优）

Fibonacci数列 ：无穷数列【1 1 2 3 5 8 13 21 34 55…】称为Fibonacci数列，在Fibonacci数列中从第三个数字开始，每一个数字都是前两个数字之和，这是一个典型的递归问题，其递归定义式如下

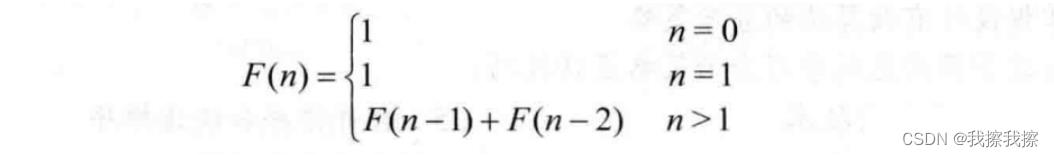
这是一个经典的动态规划问题。接下来我们将逐步分析，通过这个例子来说明重叠子问题应该如何解决

（1）暴力递归

在（算法设计与分析）第二章递归与分治策略-第一节：递归和典型递归问题这一节我们就说到过它的递归解法，如下

class Fib_Recurse
public:
    int fib(int n)
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        return fib(n - 1) + fib(n - 2);
    

;
int main() 
    Fib_Recurse fibRecurse;
    int ret = fibRecurse.fib(10);
    cout << ret << endl;

但暴力递归时间复杂度非常高，而且随着问题规模$n$变大，甚至可能会出现在规定时间内无法解出的情况。究其本质，是因为在划分问题时划分出了很多重叠的子问题，这些子问题会重复计算，因而提高了时间复杂度

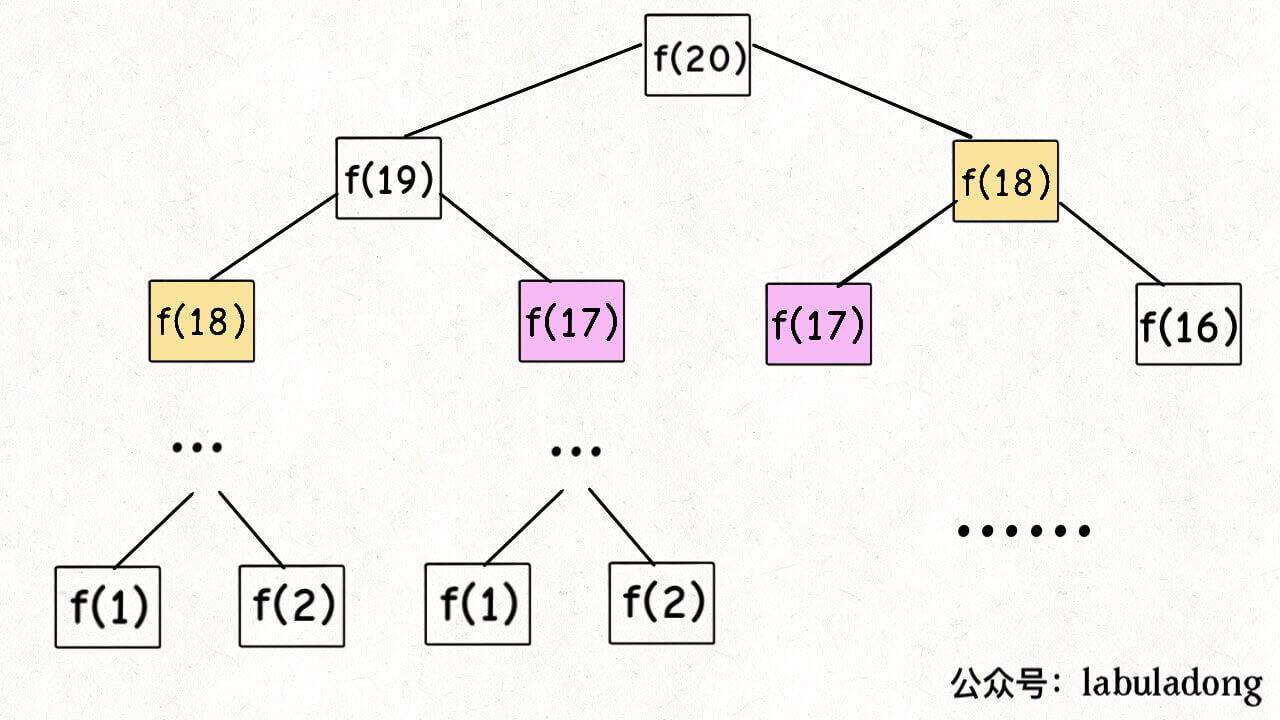
• 下图是在递归过程中形成的一颗二叉树，称之为递归树

如下图，想要计算fib(20)，就先要计算fib(19)和fib(18)，计算fib(19)又要计算fib(18)和fib(17)… …但是很明显，图中的f(18),f(17)是不需要重复计算的。虽然这张图中只画出了一部分，但是你应该明白，这颗递归树要是完全展开，那是很恐怖的，计算了相当多的重复子问题。因而这种暴力递归极其低效

（2）带有表的递归解法

既然耗时多的原因是因为重叠子问题太多，根据动态规划基本思想，我们可以这样：把fib(18)计算完之后，存储在一个表中，等下次用到fib(18)的时候，直接从备忘录查找即可

• 这个表可以用很多方式实现，最常见的便是数组和哈希表

class Fib_Optimize
public:

    int back(vector<int> &table, int n)
        if(n ==1 || n == 2) return 1;
        if(table[n] != 0)
            //如果表中有元素那么直接取得即可
            return table[n];
        
        //保存在表中
        table[n] = back(table, n-1) + back(table, n-2);
        return table[n];
    

    int fib(int n)
        if (n == 0)
            return 0;
        
        table.resize(n+1, 0);
        vector<int> table(n+1, 0);
        return back(table, n);
    

private :
    vector<int> table;
;


int main() 
    Fib_Optimize fibOptimize;
    int ret = fibOptimize.fib(10);
    cout << ret << endl;

观察这种解法的递归树，你会发现，引入表后相当于对二叉树进行了 “剪枝” 操作，大大减少了重叠子问题

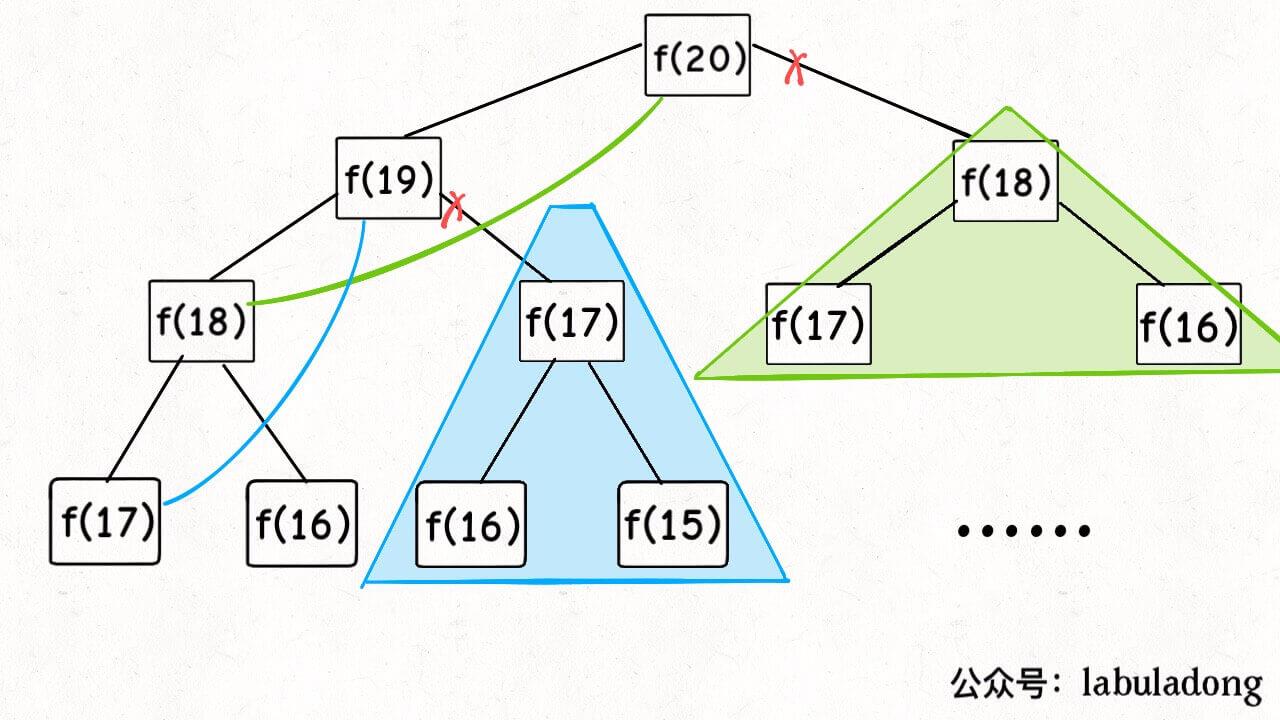
如下，通过对比这两种解法的运行时间也能很明显的感受到时间复杂度大大降低

#include <iostream>
#include <vector>
#include <ctime>
using namespace std;


class Fib_Recurse
public:
    int fib(int n)
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        return fib(n - 1) + fib(n - 2);
    

;


class Fib_Optimize
public:

    int back(vector<int> &table, int n)
        if(n ==1 || n == 2) return 1;
        if(table[n] != 0)
            //如果表中有元素那么直接取得即可
            return table[n];
        
        //保存在表中
        table[n] = back(table, n-1) + back(table, n-2);
        return table[n];
    

    int fib(int n)
        if (n == 0)
            return 0;
        
        table.resize(n+1, 0);
        vector<int> table(n+1, 0);
        return back(table, n);
    

private :
    vector<int> table;
;


int main() 
    const int N = 45; //第45个斐波那契数
    Fib_Recurse fibRecurse; // 暴力递归解法
    Fib_Optimize fibOptimize; // 带有表的递归解法
    clock_t startTime, endTime;

    startTime = clock();
    int ret_recurse = fibRecurse.fib(N);
    endTime = clock();
    cout << "使用暴力递归解法用时：" << (endTime - startTime) << " ms；" << "第" << N << "个斐波那契数是" << ret_recurse << endl;

    startTime = clock();
    int ret_optimize = fibOptimize.fib(N);
    endTime = clock();
    cout << "使用带有表的递归解法用时：" << (endTime - startTime) << " ms；" << "第" << N << "个斐波那契数是" << ret_optimize << endl;

到此为止其实我们已经用动态规划解决了这个问题，但是这和一般的动态规划还有所区别。因为现在这种解决方法是自顶向下，而一般的动态规划的题目则是自底向上的

（3）动态规划解法

仍然使用一张表，自底向上，不断迭代求解。这张表会不断保存此阶段的最优结果，也即最优子结构。下面的代码便展示了动态规划类题目代码的特点

• 会对table的初始情况进行赋值，就像台阶一样，一步一步向上迭代
• 有一个或多个for循环，它指的就是迭代过程，也即填表过程
• 数组赋值，也即转移方程，这是动态规划的核心，它决定了整个迭代过程中每一步是否能保持最优。如果转移方程写错，那么动态规划结果肯定错误，所以这一部分是最难思考的

class Fib_Dp
public:
    int fib(int n)
        if(n == 0) return 0;
        if(n==1 || n==2) return 1;
        table.resize(n+1, 0);
        //最简单的情况，也即初始情况
        table[1] = 1;
        table[2] = 2;

        //动态规划核心，填表过程
        for(int i = 3; i < n; i++)
            table[i] = table[i-1] + table[i-2]; //核心中的核心，转移方程
        

        return table[n-1];

    
private:
    vector<int> table;

;

至此我们已经解决了重叠子问题，关于如何解决最优子结构会在（算法设计与分析）第三章动态规划-第一节2：动态规划之使用“找零钱”问题说明最优子结构如何解决中说明

（4）补充：关于斐波那契数列的极致解法（时间和空间均最优）

对于这个例子，可以对空间复杂度继续优化。仔细观察你会发现：当前状态仅仅和前两个状态有关，所以我们可以放弃数组，直接使用两个变量，交替保存即可

class Solution 
public:
    int fib(int n) 
    
        if (n==0) return 0;
        if (n==1 || n==2) return 1;
        int prev=1;int curr=1;
        for(int i=3;i<=n;i++)
        
            int sum=prev+curr;
            prev=curr;
            curr=sum;
        
        return curr;
    
;

这提示我们：如果迭代的过程过程中只需要table的部分数据，那么就可以对table进行压缩，以此对空间进行优化