常见回归和分类损失函数比较

Posted 2022-12-04 沈子恒

文章转自知乎作者wdmad，更多内容建议阅读原文：https://zhuanlan.zhihu.com/p/36431289

本博文属于阅读笔记，融合了个人观点。

1. 损失函数

损失函数的一般表示为 L(y,f(x))，用以衡量真实值 y和预测值 f(x)之间不一致的程度，一般越小越好。为了便于不同损失函数的比较，常将其表示为单变量的函数，在回归问题中这个变量为 [y-f(x)] ：残差表示，在分类问题中则为 yf(x) ： 趋势一致。

2. 回归问题的损失函数

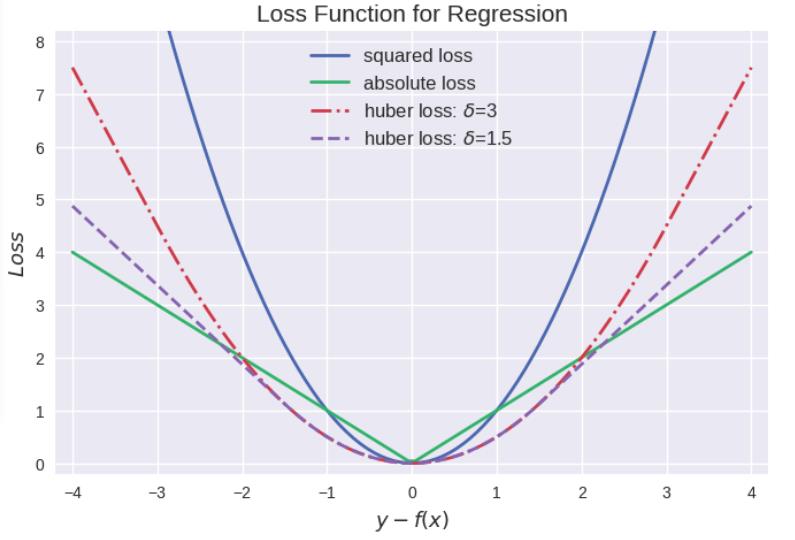
回归问题中 y 和 f(x)皆为实数 R，因此用残差 [y-f(x)]来度量二者的不一致程度。残差 (的绝对值) 越大，则损失函数越大，学习出来的模型效果就越差（这里不考虑正则化问题）。

常见的回归损失函数：

• 平方损失 (squared loss) ：

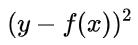
• 绝对值 (absolute loss) : 

• Huber损失 (huber loss) : 

规律总结：

1. 平方损失最常用，其缺点是对于异常点会施以较大的惩罚，因而不够robust。
2. 绝对损失具有抵抗异常点干扰的特性，但是在y-f(x)处不连续可导，难以优化。
3. Huber损失是对二者的综合，当 |y-f(x)|小于一个事先指定的值 δ时，变为平方损失；大于δ时，则变成类似于绝对值损失，因此也是比较robust的损失函数。

3. 分类问题的损失函数

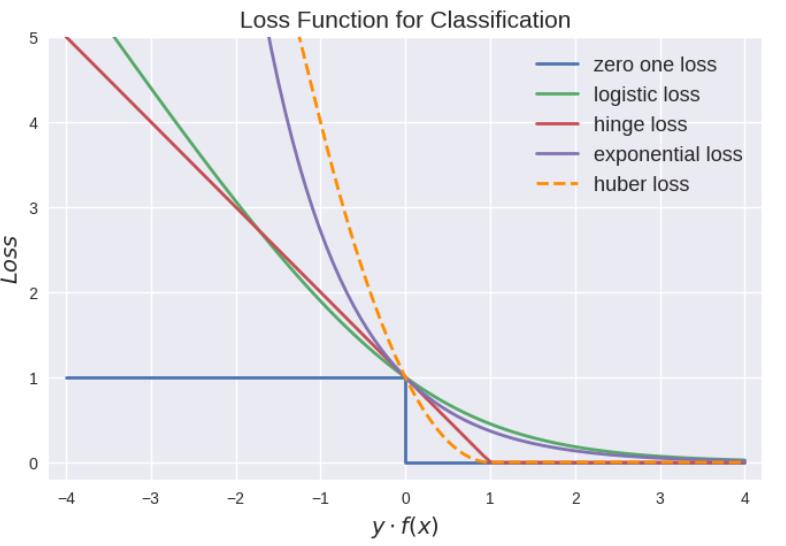
yf(x)被称为margin，其作用类似于回归问题中的y-f(x)。

二分类问题中的分类规则通常为:

可以看到如果 yf(x)>0，则样本分类正确， yf(x)<0则分类错误，而相应的分类决策边界即为 f(x)=0。所以最小化损失函数也可以看作是最大化margin的过程，任何合格的分类损失函数都应该对margin<0的样本施以较大的惩罚。

• 0-1损失 (zero-one loss):

0-1损失对每个错分类点都施以相同的惩罚，这样那些“错的离谱“(即 margin→∞) 的点并不会收到大的关注，这在直觉上不是很合适。另外0-1损失不连续、非凸，优化困难，因而常使用其他的代理损失函数进行优化。

• Logistic loss：

ogistic Loss为Logistic Regression中使用的损失函数。

• Hinge loss：

hinge loss为svm中使用的损失函数，hinge loss使得 yf(x)>1的样本损失皆为0，由此带来了稀疏解，使得svm仅通过少量的支持向量就能确定最终超平面。

推导过程：

可以看到 svm 这个形式的损失函数是自带参数w 的 L2正则的，而相比之下Logistic Regression的损失函数则没有显式的正则化项，需要另外添加。

• 指数损失(Exponential loss)

exponential loss为AdaBoost中使用的损失函数，使用exponential loss能比较方便地利用加法模型推导出AdaBoost算法 。然而其和squared loss一样，对异常点敏感，不够robust。

• modified Huber loss

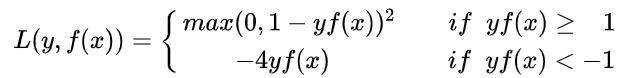
modified huber loss结合了hinge loss和logistic loss的优点，既能在 yf(x)>1时产生稀疏解提高训练效率，又能进行概率估计。另外其对于  yf(x)<-1样本的惩罚以线性增加，这意味着受异常点的干扰较少，比较robust。