论文解读：Improving Color Reproduction Accuracy on Cameras

Posted 2022-12-04 Matrix_11

论文解读：Improving Color Reproduction Accuracy on Cameras

今天介绍一篇有关颜色准确性的文章，颜色的准确性是个有点玄妙的问题，因为人眼独特的颜色感知机制，导致人眼对不同光照下的物体有一种常恒性，简单来说，就是红色的苹果，在不同光照下，对人眼来说都是一样的红色，但是对相机来说不是这样的，相机反映的是真实的光谱性质，为了配合人眼的这种感知特性，就需要对颜色做一些校正或者变换，使得颜色在人眼看来是准确的，这个准确，不一定反映了场景的客观真实。

颜色导论

在介绍这篇文章之前，我们先简单介绍一下颜色的基本知识，我们通常说的颜色，可以简单看成是可见光的光谱，我们知道彩虹有红，橙，黄，绿，青，蓝，紫几种颜色，分别对应着不同的光谱，自然界有发光的物体，我们称为光源，比如太阳，自己会发光，还有人造光源，比如电灯什么的，也可以发光，发光体会发出不同光谱的光，除此之外，自然界的物体也会吸收光和反射光，有些物体虽然自己不会发光，但是会反射光线，这样也可以让人眼感知到，人眼是怎么感知颜色的呢，因为人眼的视网膜上，密密麻麻地分布着很多感光细胞，这些细胞，主要分成两大类，一类称为柱状细胞，一类称为锥状细胞，柱状细胞主要是感知亮度变化的，而锥状细胞就是用来感知颜色变化的，锥状细胞有三种，分别对应长，中，短三种波长的光谱，也就是我们常说的红，绿，蓝。这些感光细胞，对不同光谱的光，会产生不同的应激响应，从而得到不同的色彩感知，所以这个过程有点像个滤波器滤波，人眼的感光细胞就类似滤波器，只对特定频率的光谱会产生响应，而其他频率的光谱都被忽略掉了，所以虽然真实世界里，光谱是各种各样的，但是人眼能够感受到的只是很小的一部分。

在 20 世纪二三十年代，已经有人对人类的颜色感知进行量化的标定，最早是基于 r,g,b 三种颜色进行标定，后来改成了标准的 XYZ，基于三条光谱感知曲线，只有知道环境中光线的 SPD 曲线，就可以得到最终感知的亮度：

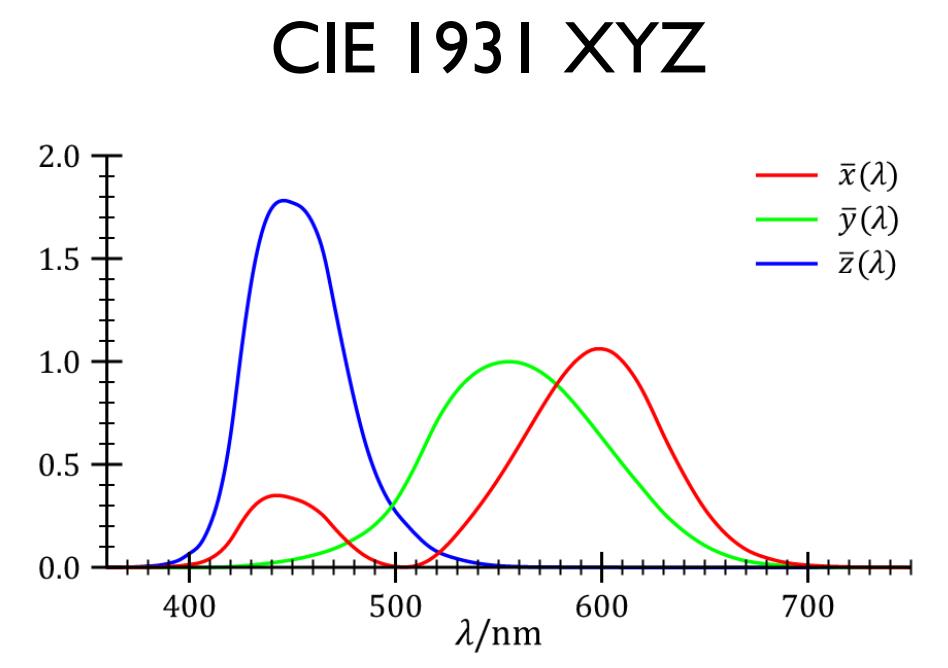
• 插入图片 2， X,Y,Z 光谱感知曲线

$$\begin{gathered} X={\int }_{380}^{780}I(\lambda )\bar{x}(\lambda )d\lambda \\ Y={\int }_{380}^{780}I(\lambda )\bar{y}(\lambda )d\lambda \\ Z={\int }_{380}^{780}I(\lambda )\bar{z}(\lambda )d\lambda \end{gathered}$$

再根据 XYZ 与 RGB 之间的转换关系，就能得到最终的 RGB 值。

上面介绍的是人眼对颜色的感知，总的来说就是环境中光线的 SPD 与人眼的光谱感知曲线的一个积分，而 sensor 也是有自己的感知曲线的，一般来说，sensor 感知曲线与环境中的光线 SPD 做积分，就是 sensor 对环境光线的一个响应，sensor 上的每个 pixel 也有一个光谱响应曲线，对不同光谱的光会有不同的响应，而且每个相机的 sensor 由于制造的不同，响应也有可能存在差异，所以我们看不同的相机拍摄同一个场景的时候，颜色会有一些差异，而且与人眼感知相比，也存在差异，所以说，在 ISP 里面，颜色校正是非常重要的一个环节，终极目的，就是希望能把相机 sensor 上感应的颜色与人眼感知的色彩匹配上。这也就是我们常说的白平衡校正以及颜色转换。这两步的最终目的都是为了把颜色恢复地准确。人眼有一种非常神奇的特性，就是颜色常恒性，为了将场景中的颜色与人眼感知的一致，多少研究者绞尽脑汁，到目前为止，也不能说做得特别好。

颜色的校正主要分两大块，白平衡 white balance 和颜色转换 color calibration

• 插入图片 ISP 中的颜色校正流程，包括颜色的准确性和颜色的增强

白平衡就是为了解决颜色常恒性问题的，因为人眼在不同光照下对同一个物体的颜色感知基本是一样的，就像红色的苹果在阳光下，阴天以及日光灯下对人眼来说都是红色的，但是对相机来说，那就不是了，因为相机是完全按照真实光线的光谱与自身的光谱曲线积分得到的，反映的是客观的成像，人眼自己做了一些变化。

• 插入图片，颜色常恒性
  

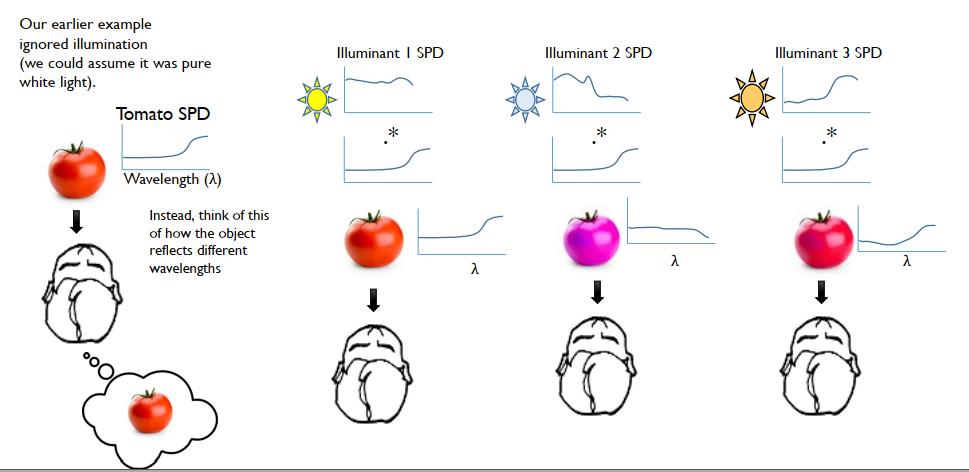
白平衡主要分成两部分，一部分是光照的估计，也就是我们说的色温估计，然后就是一个校正，一般来说就是三个通道乘以不同的 gain 值，因为每个不同色温下都有一个对应的校正系数，这都是提前标定出来的，所以一旦估计出了环境中的色温，就直接乘以校正系数就算完成了白平衡的校正。白平衡做完之后，一般后面会再接一个 color calibration，这步就是为了把 sensor 的 RGB 空间转换到人眼感知的 RGB 空间，我的理解是白平衡是为了消除不同光源的影响，而颜色转换是让颜色符合人眼的感知。

假设 ${\mathbf{C}}_{cam}$ 表示相机 sensor 上三个通道对环境光谱的响应，那么其维度是 $3\times N$，3 表示 R,G,B 三个通道，N 表示不同光谱的个数，将环境中的所有物体表示为 $\mathbf{R}$, 每一列表示物体对不同光谱光线的反射强度, 那么每一列可以表示为 ${\mathbf{r}}_i$，每一列的维度为 N，同时假设环境中的光源为 $\mathbf{l}$，那么相机 sensor 的响应可以表示为：

$${\mathbf{\Phi }}_{cam}^{\mathbf{l}}={\mathbf{C}}_{cam}\text{diag}(\mathbf{l})\mathbf{R}$$

$\mathbf{l}$ 也是一个 N 维的列向量，表示该光源在不同频率下的强度，diag 表示对角化。

而我们最终的目标是希望将相机 sensor 感知的颜色变换到人眼感知的颜色空间，如下所示：

$${\mathbf{\Phi }}_{xyz}={\mathbf{C}}_{xyz}\mathbf{R}$$

为了实现这个目的，第一步就是我们说的去除光照影响，一般来说，需要求解如下的优化函数：

$$W_F=\underset{W_F}{\mathrm{argmin}}||{\mathbf{C}}_{cam}\mathbf{R}-W_F{\mathbf{\Phi }}_{cam}^{\mathbf{l}}|{|}^2$$

$W_F$ 表示使得观测到的物体在某个光照下与标准光照下的该物体的颜色误差最小，不过目前最常用的估计方法就是针对灰度物体进行测算，所以最后得到的系数矩阵是一个对角矩阵：

$$W_D=\text{diag}({\mathbf{C}}_{cam}\mathbf{l}{)}^{-1}$$

其中 $\mathbf{l}$ 表示观测到的环境光照，$W_D$ 是一个对角矩阵，与 $W_F$ 是全系数矩阵不同，$W_D$ 对某些颜色的像素的校正并不正确。

白平衡做完之后，接下来就是 Color space transform (CST)，需要将 sensor 的 RGB 空间转换到人眼感知的色彩空间，一般都是通过标准色板来进行标定：

$$T_{\mathbf{l}}=\underset{T_{\mathbf{l}}}{\mathrm{argmin}}||{\mathbf{C}}_{xyz}\mathbf{R}-T_{\mathbf{l}}{W}_D^{\mathbf{l}}{\mathbf{\Phi }}_{cam}^{\mathbf{l}}|{|}^2$$

因为这个是和环境光照的色温有关的，所以需要对不同色温下的光照进行标定。

文章中说目前常用的方法是对两种色温下的系数进行标定，一般是 2500K 和 6500K 下的色温做标定，然后再根据当前色温进行插值：

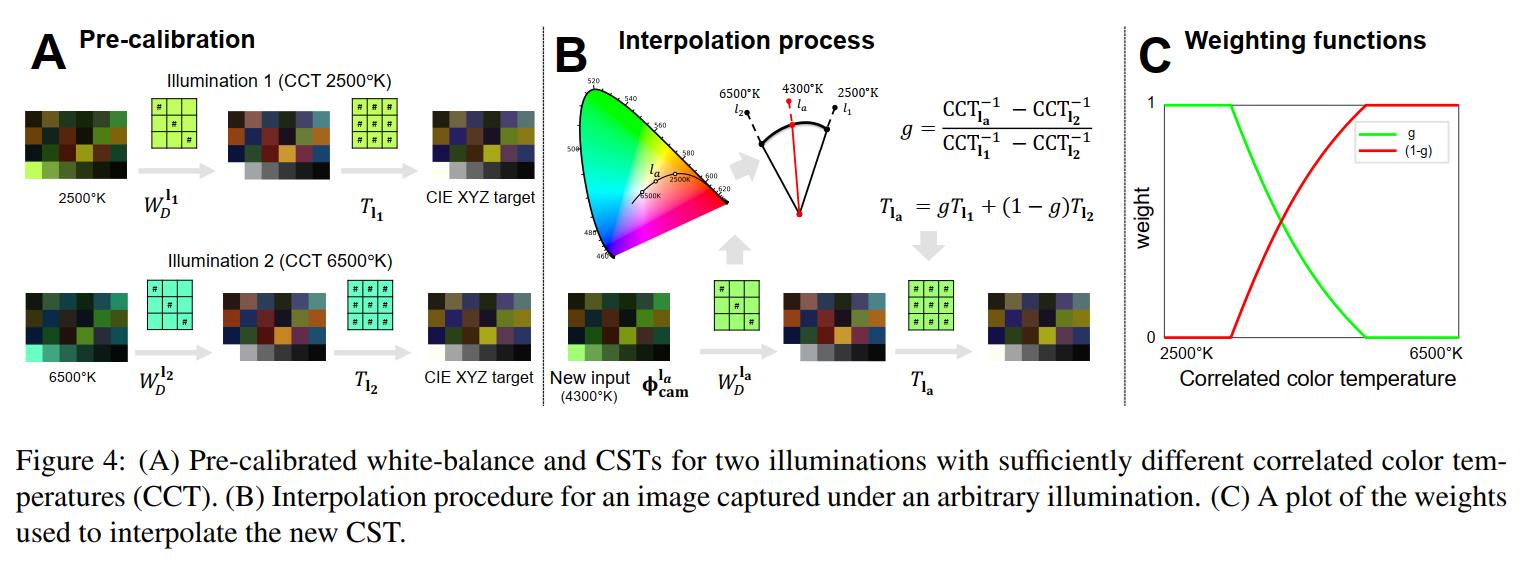
• 插入图片，利用三个标定系数进行插值

$$T_{\mathbf{l}}=g{T}_{{\mathbf{l}}_1}+(1-g)T_{{\mathbf{l}}_2}$$

$g$ 就是融合的系数。

文章里提到的一个方法，就是多增加一个标准的转换系数，比如 5000 K 的时候也先进行标定，这样似乎插值的时候会更准确一些，然后另外一种方法就是用全系数矩阵，前面介绍过，对角系数的白平衡系数矩阵对有颜色的像素的校正效果不是很好，如果能将对角系数换成全系数，那么对颜色的校正效果将会更好，文章用如下的优化方程进行优化求解：

$$T_{fixed}=\underset{T}{\mathrm{argmin}}||\sum _i({\mathbf{C}}_{xyz}\mathbf{R}-T{W}_F^{{\mathbf{l}}_i}$$

翻译 | Improving Distributional Similarity with Lessons Learned from Word Embeddings

Improving Knowledge Tracing via Pre-training Question Embeddings

为自己定义每个python类添加__repr__和__str__

BERT - 论文解读

LipNet 论文解读