Hilbert曲线简介及生成算法

Posted 2022-12-04 周旭光

Hilbert曲线

 

Hilbert曲线是一种填充曲线，类似的填充曲线还包括Z曲线，格雷码等其他方法。Hilbert曲线依据自身空间填充曲线的特性，可以线性地贯穿二维或者更高维度每个离散单元，并且仅仅穿过一次，并对每个离散单元进行线性排序和编码，该编码作为该单元的唯一标识。空间填充曲线可以将高维空间中没有良好顺序的数据映射到一维空间，经过这种编码方式，空间上相邻的对象会邻近存储在一块，可以减少IO的时间，提高内存中数据处理效率。

Hilbert曲线如下图所示：

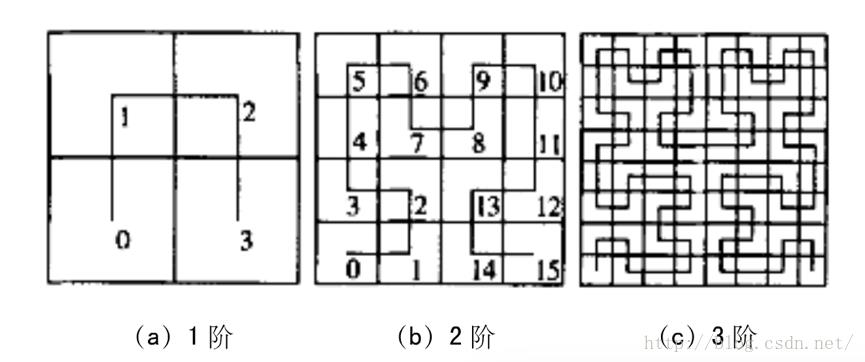
Hilbert作用非常大，除了上面讲到的作为一种基于网格的空间索引外，还可以用作图像数据的混淆或者加密。

 

Hilbert曲线生成的关键是如何计算每一个离散单元所对应的编码以及根据编码获得离散单元所处的位置。代码如下：

void rot(int n, int *x, int *y, int rx, int ry);

//XY坐标到Hilbert代码转换
int xy2d (int n, int x, int y)

    int rx, ry, s, d=0;
    for (s=n/2; s>0; s/=2)
    
        rx = (x & s) > 0;
        ry = (y & s) > 0;
        d += s * s * ((3 * rx) ^ ry);
        rot(s, &x, &y, rx, ry);
    
    return d;


//Hilbert代码到XY坐标
void d2xy(int n, int d, int *x, int *y)

    int rx, ry, s, t=d;
    *x = *y = 0;
    for (s=1; s<n; s*=2)
    
        rx = 1 & (t/2);
        ry = 1 & (t ^ rx);
        rot(s, x, y, rx, ry);
        *x += s * rx;
        *y += s * ry;
        t /= 4;
    


void rot(int n, int *x, int *y, int rx, int ry)

    if (ry == 0)
    
        if (rx == 1)
        
            *x = n-1 - *x;
            *y = n-1 - *y;
        

        //Swap x and y
        int t  = *x;
        *x = *y;
        *y = t;
    

代码是维基百科上，结果可靠。上面的代码需要注意的是，变量n是网格在X方向或者Y方向上单元的个数，n必须是2的次方，如果原始的图像宽高数并不是2的次方，那么就需要求出最接近2的某个次方的数。

 

参考文献：

地理信息系统算法基础

https://en.wikipedia.org/wiki/Hilbert_curve- Applications_and_mapping_algorithms