矩阵乘法python的实现
Posted 道亦无名
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵乘法python的实现相关的知识,希望对你有一定的参考价值。
两个矩阵相乘得到第三个矩阵,我们需要 A 的形状为 m × n,B 的形状为 n × p,得到的矩阵为 C 的形状为 m × p:C = AB
注意矩阵乘法不是元素对应相乘,元素对应相乘又叫 Hadamard 乘积,记作 A ⊙ B。
向量可以看作是列为 1 的矩阵,两个相同维数的向量 x 和 y 的点乘(Dot Product)或者内积。
我们也可以把矩阵乘法理解为:Ci,j 表⽰ A 的第 i ⾏与 B 的第 j 列的点积。
具体的示范代码如下:
from mxnet import np, npx
x = np.array([[1.2,2.2],[3.0,4.0]])
y = np.array([[2.2,3.2],[4.0,5.0]])
print("矩阵乘法:", np.dot(x,y))
print("元素相乘:", np.multiply(x,y))
print("逐个元素相乘:", x*y)
v1 = np.array([3.0,4.0])
v2 = np.array([5.0,6.0])
print("向量内积:", np.dot(v1,v2))
执行效果如下:
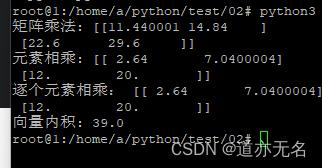
以上是关于矩阵乘法python的实现的主要内容,如果未能解决你的问题,请参考以下文章