备战数学建模45-模拟退火算法SA(攻坚站9)
Posted nuist__NJUPT
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了备战数学建模45-模拟退火算法SA(攻坚站9)相关的知识，希望对你有一定的参考价值。
模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis [1] 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。
目录
一、模拟退火算法
1.1、模拟退火算法基本原理
启发式搜索算法，模拟退火算法就是启发式搜索算法中的一种。（其他你可能感兴趣的启发式搜索算法：粒子群、遗传、蚁群等），启发式算法：在搜索最优解的过程中利用到了原来搜索过程中得到的信息，且这个信息会改进我们的搜索过程。（深刻体会这句话！！！）
模拟退火就是模拟金属退火过程进行启发式地搜索全局最优解的过程，具体如如下：
- 模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能。
- 赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。
为了保证搜索过程的彻底，在同一温度下（同一个小 t）我们需要进行多次搜索（例如重复上面的流程 500 次）；之后我们降低温度，然后再来进行新的一轮搜索。
什么时候停止搜索？
很多种准则：（1）达到指定的迭代次数，例如迭代 200 次；（2）达到指定的温度，例如
温度小于 0.000001；（3）我们找到的最优解连续 M（例如 30 次）次迭代都没有变化
怎么样在 A 附近随机生成一个新解 B 呀？即新解应该怎么样生成？
答案：没有统一规定，需要具体问题具体分析。
也可以看这个过程，就是先设置初始温度和初始解，然后温度衰减，模拟降温，然后根据当前解最新解，如果最新解比之前的解更好，则接受，否则，按一定的概率接受。
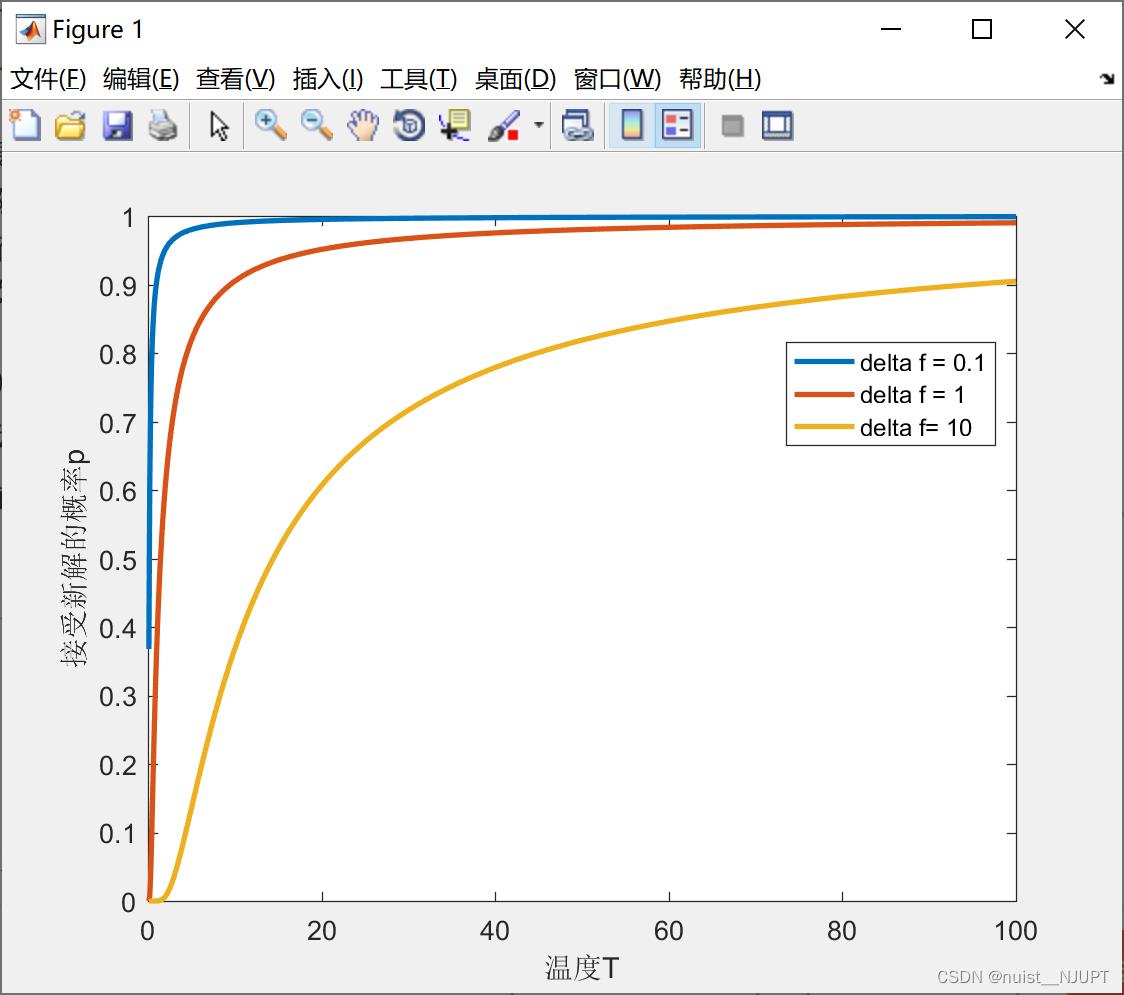
（1）温度一定时， ∆𝒇越小，概率越大，即目标函数相差越小接受的可能性越大。
（2）∆𝒇一定时，温度越高，概率越大，即搜索前期温度较高时更有可能接受新解。
下面要看一下模拟退火设置温度初值T0的问题，一般100~1000之间，不宜过大，也不宜过小。另外对于温度衰减系数一般取0.95.
1.2、模拟退火算法求解函数最值问题
我们看一下用模拟退火算法求解一元函数最大值问题，在指定区间内的最大值。
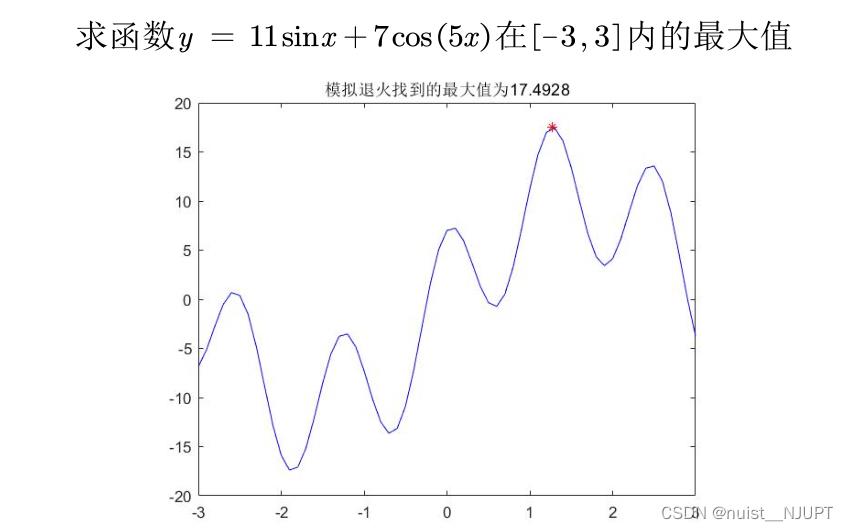
因为我们需要每次产生新的解，新解都有一定的产生规则，我们每个新解xnew=x+T*z
下面看一下具体的matlab代码，具体的代码如下：
%% SA 模拟退火: 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值(动画演示）
tic
clear; clc
%% 绘制函数的图形
x = -3:0.1:3;
y = 11*sin(x) + 7*cos(5*x);
figure
plot(x,y,'b-')
hold on % 不关闭图形，继续在上面画图
%% 参数初始化
narvs = 1; % 变量个数
T0 = 100; % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
Lk = 100; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
x_lb = -3; % x的下界
x_ub = 3; % x的上界
%% 随机生成一个初始解
x0 = zeros(1,narvs);
for i = 1: narvs
x0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun1(x0); % 计算当前解的函数值
h = scatter(x0,y0,'*r'); % scatter是绘制二维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
%% 定义一些保存中间过程的量，方便输出结果和画图
max_y = y0; % 初始化找到的最佳的解对应的函数值为y0
MAXY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的max_y (方便画图）
%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数
for i = 1 : Lk % 内循环，在每个温度下开始迭代
y = randn(1,narvs); % 生成1行narvs列的N(0,1)随机数
z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算z
x_new = x0 + z*T; % 根据新解的产生规则计算x_new的值
% 如果这个新解的位置超出了定义域，就对其进行调整
for j = 1: narvs
if x_new(j) < x_lb(j)
r = rand(1);
x_new(j) = r*x_lb(j)+(1-r)*x0(j);
elseif x_new(j) > x_ub(j)
r = rand(1);
x_new(j) = r*x_ub(j)+(1-r)*x0(j);
end
end
x1 = x_new; % 将调整后的x_new赋值给新解x1
y1 = Obj_fun1(x1); % 计算新解的函数值
if y1 > y0 % 如果新解函数值大于当前解的函数值
x0 = x1; % 更新当前解为新解
y0 = y1;
else
p = exp(-(y0 - y1)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
x0 = x1; % 更新当前解为新解
y0 = y1;
end
end
% 判断是否要更新找到的最佳的解
if y0 > max_y % 如果当前解更好，则对其进行更新
max_y = y0; % 更新最大的y
best_x = x0; % 更新找到的最好的x
end
end
MAXY(iter) = max_y; % 保存本轮外循环结束后找到的最大的y
T = alfa*T; % 温度下降
pause(0.01) % 暂停一段时间(单位：秒)后再接着画图
h.XData = x0; % 更新散点图句柄的x轴的数据（此时解的位置在图上发生了变化）
h.YData = Obj_fun1(x0); % 更新散点图句柄的y轴的数据（此时解的位置在图上发生了变化）
end
disp('最佳的位置是：'); disp(best_x)
disp('此时最优值是：'); disp(max_y)
pause(0.5)
h.XData = []; h.YData = []; % 将原来的散点删除
scatter(best_x,max_y,'*r'); % 在最大值处重新标上散点
title(['模拟退火找到的最大值为', num2str(max_y)]) % 加上图的标题
%% 画出每次迭代后找到的最大y的图形
figure
plot(1:maxgen,MAXY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc下面再看一下模拟退火求解二元函数最值问题，具体的matlab代码如下：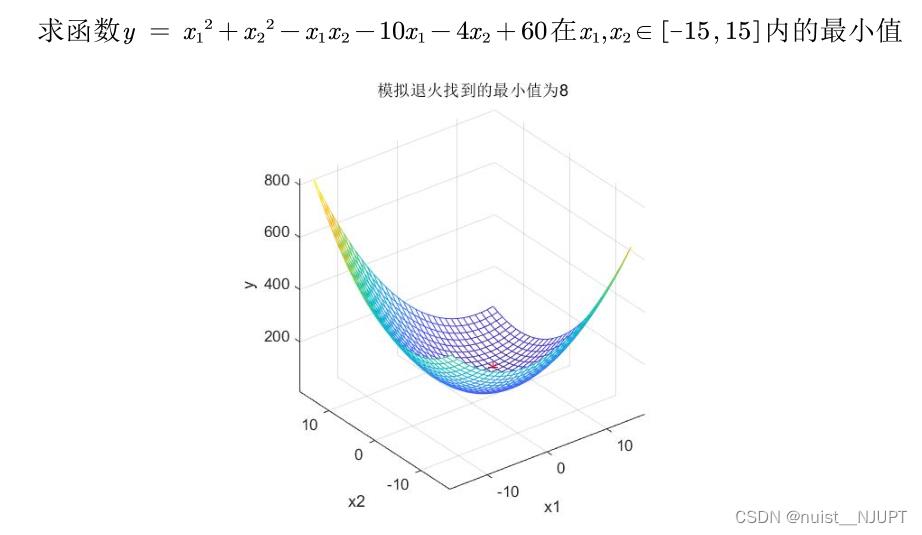
%% SA 模拟退火: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示）
tic
clear; clc
%% 绘制函数的图形
figure
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on % 不关闭图形，继续在上面画图
%% 参数初始化
narvs = 2; % 变量个数
T0 = 100; % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
Lk = 100; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
%% 随机生成一个初始解
x0 = zeros(1,narvs);
for i = 1: narvs
x0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun2(x0); % 计算当前解的函数值
h = scatter3(x0(1),x0(2),y0,'*r'); % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
%% 定义一些保存中间过程的量，方便输出结果和画图
min_y = y0; % 初始化找到的最佳的解对应的函数值为y0
MINY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_y (方便画图）
%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数
for i = 1 : Lk % 内循环，在每个温度下开始迭代
y = randn(1,narvs); % 生成1行narvs列的N(0,1)随机数
z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算z
x_new = x0 + z*T; % 根据新解的产生规则计算x_new的值
% 如果这个新解的位置超出了定义域，就对其进行调整
for j = 1: narvs
if x_new(j) < x_lb(j)
r = rand(1);
x_new(j) = r*x_lb(j)+(1-r)*x0(j);
elseif x_new(j) > x_ub(j)
r = rand(1);
x_new(j) = r*x_ub(j)+(1-r)*x0(j);
end
end
x1 = x_new; % 将调整后的x_new赋值给新解x1
y1 = Obj_fun2(x1); % 计算新解的函数值
if y1 < y0 % 如果新解函数值小于当前解的函数值
x0 = x1; % 更新当前解为新解
y0 = y1;
else
p = exp(-(y1 - y0)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
x0 = x1; % 更新当前解为新解
y0 = y1;
end
end
% 判断是否要更新找到的最佳的解
if y0 < min_y % 如果当前解更好，则对其进行更新
min_y = y0; % 更新最小的y
best_x = x0; % 更新找到的最好的x
end
end
MINY(iter) = min_y; % 保存本轮外循环结束后找到的最小的y
T = alfa*T; % 温度下降
pause(0.02) % 暂停一段时间后(单位：秒)再接着画图
h.XData = x0(1); % 更新散点图句柄的x轴的数据（此时解的位置在图上发生了变化）
h.YData = x0(2); % 更新散点图句柄的y轴的数据（此时解的位置在图上发生了变化）
h.ZData = Obj_fun2(x0); % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
disp('最佳的位置是：'); disp(best_x)
disp('此时最优值是：'); disp(min_y)
pause(0.5)
h.XData = []; h.YData = []; h.ZData = []; % 将原来的散点删除
scatter3(best_x(1), best_x(2), min_y,'*r'); % 在最小值处重新标上散点
title(['模拟退火找到的最小值为', num2str(min_y)]) % 加上图的标题
%% 画出每次迭代后找到的最小y的图形
figure
plot(1:maxgen,MINY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc1.3、模拟退火求解旅行商问题
我们再看一下模拟退火求解旅行商问题，具体如下：
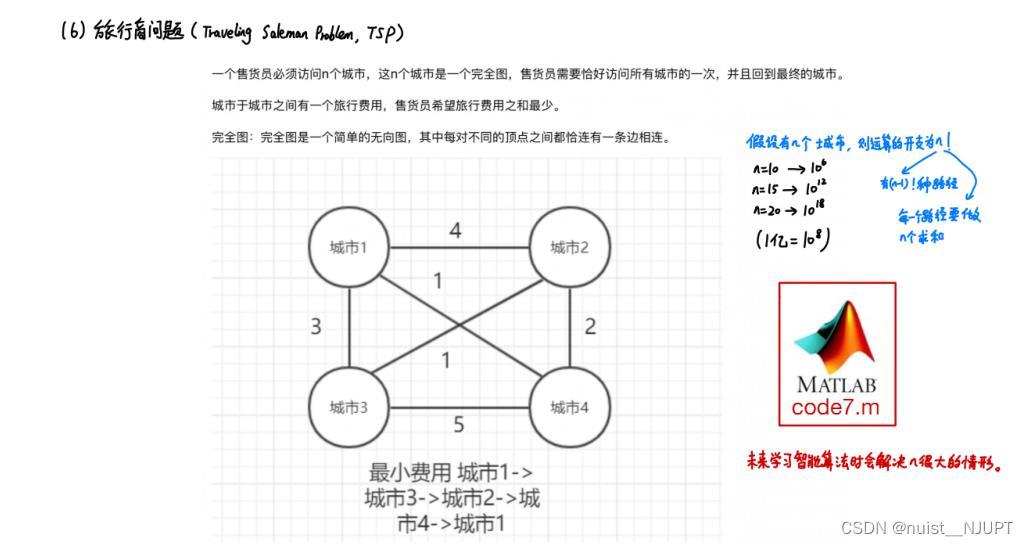
因为需要产生新解，这里提供了三种产生新解的方法，分别为交换法，移位法和倒置法。
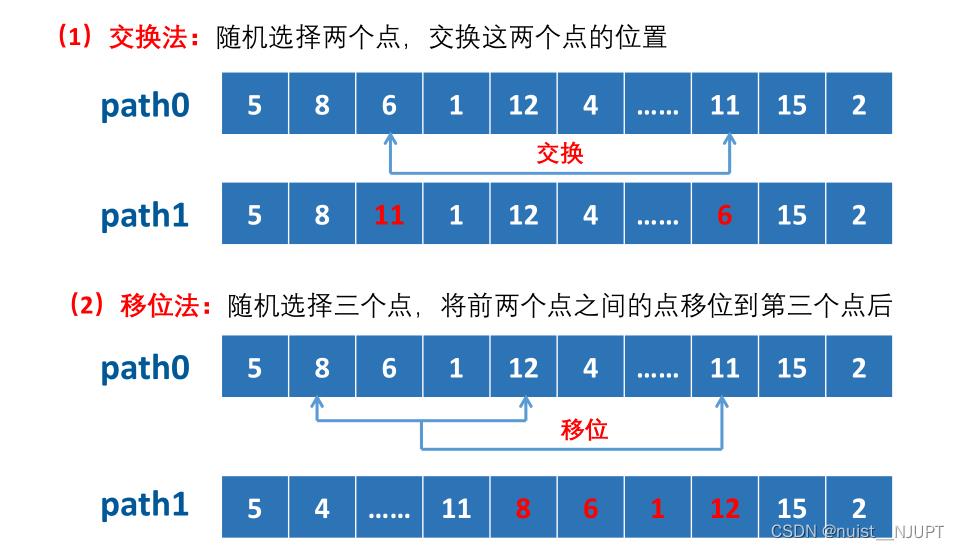
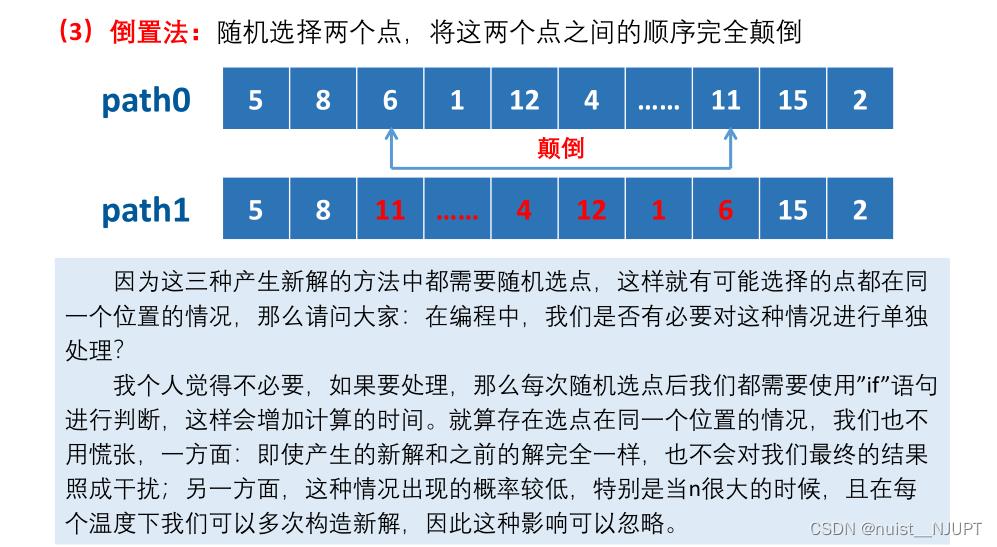模拟退火求解TSP的脚本代码如下：
%% 模拟退火解决TSP问题(很多地方我直接引用的蒙特卡罗模拟里面的代码)
tic
rng('shuffle') % 控制随机数的生成，否则每次打开matlab得到的结果都一样
% https://ww2.mathworks.cn/help/matlab/math/why-do-random-numbers-repeat-after-startup.html
% https://ww2.mathworks.cn/help/matlab/ref/rng.html
clear;clc
% 38个城市，TSP数据集网站(http://www.tsp.gatech.edu/world/djtour.html) 上公测的最优结果6656。
coord = [11003.611100,42102.500000;11108.611100,42373.888900;11133.333300,42885.833300;11155.833300,42712.500000;11183.333300,42933.333300;11297.500000,42853.333300;11310.277800,42929.444400;11416.666700,42983.333300;11423.888900,43000.277800;11438.333300,42057.222200;11461.111100,43252.777800;11485.555600,43187.222200;11503.055600,42855.277800;11511.388900,42106.388900;11522.222200,42841.944400;11569.444400,43136.666700;11583.333300,43150.000000;11595.000000,43148.055600;11600.000000,43150.000000;11690.555600,42686.666700;11715.833300,41836.111100;11751.111100,42814.444400;11770.277800,42651.944400;11785.277800,42884.444400;11822.777800,42673.611100;11846.944400,42660.555600;11963.055600,43290.555600;11973.055600,43026.111100;12058.333300,42195.555600;12149.444400,42477.500000;12286.944400,43355.555600;12300.000000,42433.333300;12355.833300,43156.388900;12363.333300,43189.166700;12372.777800,42711.388900;12386.666700,43334.722200;12421.666700,42895.555600;12645.000000,42973.333300];
n = size(coord,1); % 城市的数目
figure % 新建一个图形窗口
plot(coord(:,1),coord(:,2),'o'); % 画出城市的分布散点图
hold on % 等一下要接着在这个图形上画图的
d = zeros(n); % 初始化两个城市的距离矩阵全为0
for i = 2:n
for j = 1:i
coord_i = coord(i,:); x_i = coord_i(1); y_i = coord_i(2); % 城市i的横坐标为x_i，纵坐标为y_i
coord_j = coord(j,:); x_j = coord_j(1); y_j = coord_j(2); % 城市j的横坐标为x_j，纵坐标为y_j
d(i,j) = sqrt((x_i-x_j)^2 + (y_i-y_j)^2); % 计算城市i和j的距离
end
end
d = d+d'; % 生成距离矩阵的对称的一面
%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 1000; % 最大迭代次数
Lk = 500; % 每个温度下的迭代次数
alpfa = 0.95; % 温度衰减系数
%% 随机生成一个初始解
path0 = randperm(n); % 生成一个1-n的随机打乱的序列作为初始的路径
result0 = calculate_tsp_d(path0,d); % 调用我们自己写的calculate_tsp_d函数计算当前路径的距离
%% 定义一些保存中间过程的量，方便输出结果和画图
min_result = result0; % 初始化找到的最佳的解对应的距离为result0
RESULT = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_result (方便画图）
%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数
for i = 1 : Lk % 内循环，在每个温度下开始迭代
path1 = gen_new_path(path0); % 调用我们自己写的gen_new_path函数生成新的路径
result1 = calculate_tsp_d(path1,d); % 计算新路径的距离
%如果新解距离短，则直接把新解的值赋值给原来的解
if result1 < result0
path0 = path1; % 更新当前路径为新路径
result0 = result1;
else
p = exp(-(result1 - result0)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
path0 = path1; % 更新当前路径为新路径
result0 = result1;
end
end
% 判断是否要更新找到的最佳的解
if result0 < min_result % 如果当前解更好，则对其进行更新
min_result = result0; % 更新最小的距离
best_path = path0; % 更新找到的最短路径
end
end
RESULT(iter) = min_result; % 保存本轮外循环结束后找到的最小距离
T = alpfa*T; % 温度下降
end
disp('最佳的方案是：'); disp(mat2str(best_path))
disp('此时最优值是：'); disp(min_result)
best_path = [best_path,best_path(1)]; % 在最短路径的最后面加上一个元素，即第一个点（我们要生成一个封闭的图形）
n = n+1; % 城市的个数加一个（紧随着上一步）
for i = 1:n-1
j = i+1;
coord_i = coord(best_path(i),:); x_i = coord_i(1); y_i = coord_i(2);
coord_j = coord(best_path(j),:); x_j = coord_j(1); y_j = coord_j(2);
plot([x_i,x_j],[y_i,y_j],'-b') % 每两个点就作出一条线段，直到所有的城市都走完
% pause(0.02) % 暂停0.02s再画下一条线段
hold on
end
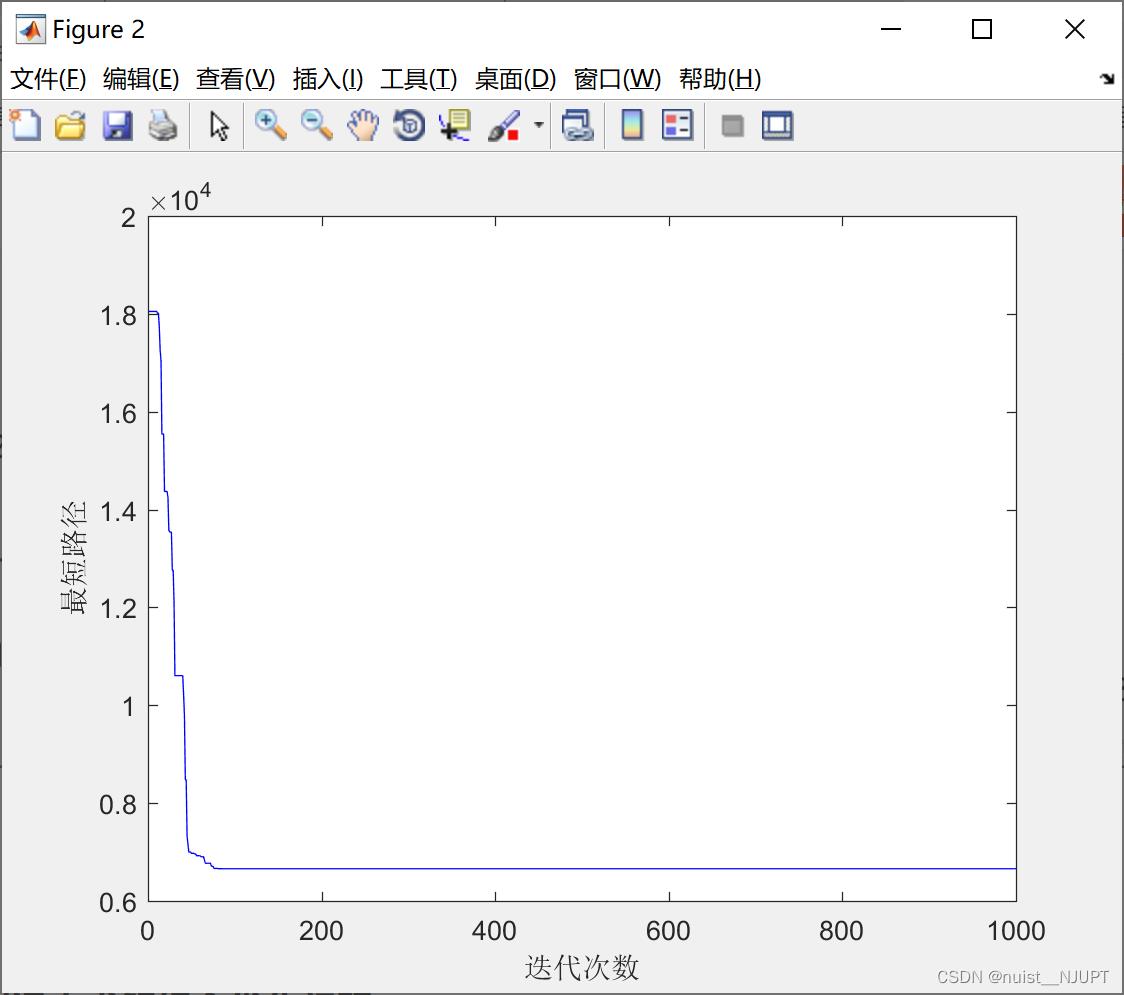
%% 画出每次迭代后找到的最短路径的图形
figure
plot(1:maxgen,RESULT,'b-');
xlabel('迭代次数');
ylabel('最短路径');
toc产生新的路径的方法，即产生新的解的方法：
function path1 = gen_new_path(path0)
% path0: 原来的路径
n = length(path0);
% 随机选择两种产生新路径的方法
p1 = 0.33; % 使用交换法产生新路径的概率
p2 = 0.33; % 使用移位法产生新路径的概率
r = rand(1); % 随机生成一个[0 1]间均匀分布的随机数
if r< p1 % 使用交换法产生新路径
c1 = randi(n); % 生成1-n中的一个随机整数
c2 = randi(n); % 生成1-n中的一个随机整数
path1 = path0; % 将path0的值赋给path1
path1(c1) = path0(c2); %改变path1第c1个位置的元素为path0第c2个位置的元素
path1(c2) = path0(c1); %改变path1第c2个位置的元素为path0第c1个位置的元素
elseif r < p1+p2 % 使用移位法产生新路径
c1 = randi(n); % 生成1-n中的一个随机整数
c2 = randi(n); % 生成1-n中的一个随机整数
c3 = randi(n); % 生成1-n中的一个随机整数
sort_c = sort([c1 c2 c3]); % 对c1 c2 c3从小到大排序
c1 = sort_c(1); c2 = sort_c(2); c3 = sort_c(3); % c1 < = c2 <= c3
tem1 = path0(1:c1-1);
tem2 = path0(c1:c2);
tem3 = path0(c2+1:c3);
tem4 = path0(c3+1:end);
path1 = [tem1 tem3 tem2 tem4];
else % 使用倒置法产生新路径
c1 = randi(n); % 生成1-n中的一个随机整数
c2 = randi(n); % 生成1-n中的一个随机整数
if c1>c2 % 如果c1比c2大，就交换c1和c2的值
tem = c2;
c2 = c1;
c1 = tem;
end
tem1 = path0(1:c1-1);
tem2 = path0(c1:c2);
tem3 = path0(c2+1:end);
path1 = [tem1 fliplr(tem2) tem3]; %矩阵的左右对称翻转 fliplr，上下对称翻转 flipud
end
end计算新的路径的距离的方法，具体如下：
function result = calculate_tsp_d(path,d)
% 输入：path:路径（1至n的一个序列），d：距离矩阵
n = length(path);
result = 0; % 初始化该路径走的距离为0
for i = 1:n-1
result = d(path(i),path(i+1)) + result; % 按照这个序列不断的更新走过的路程这个值
end
result = d(path(1),path(n)) + result; % 别忘了加上从最后一个城市返回到最开始那个城市的距离
end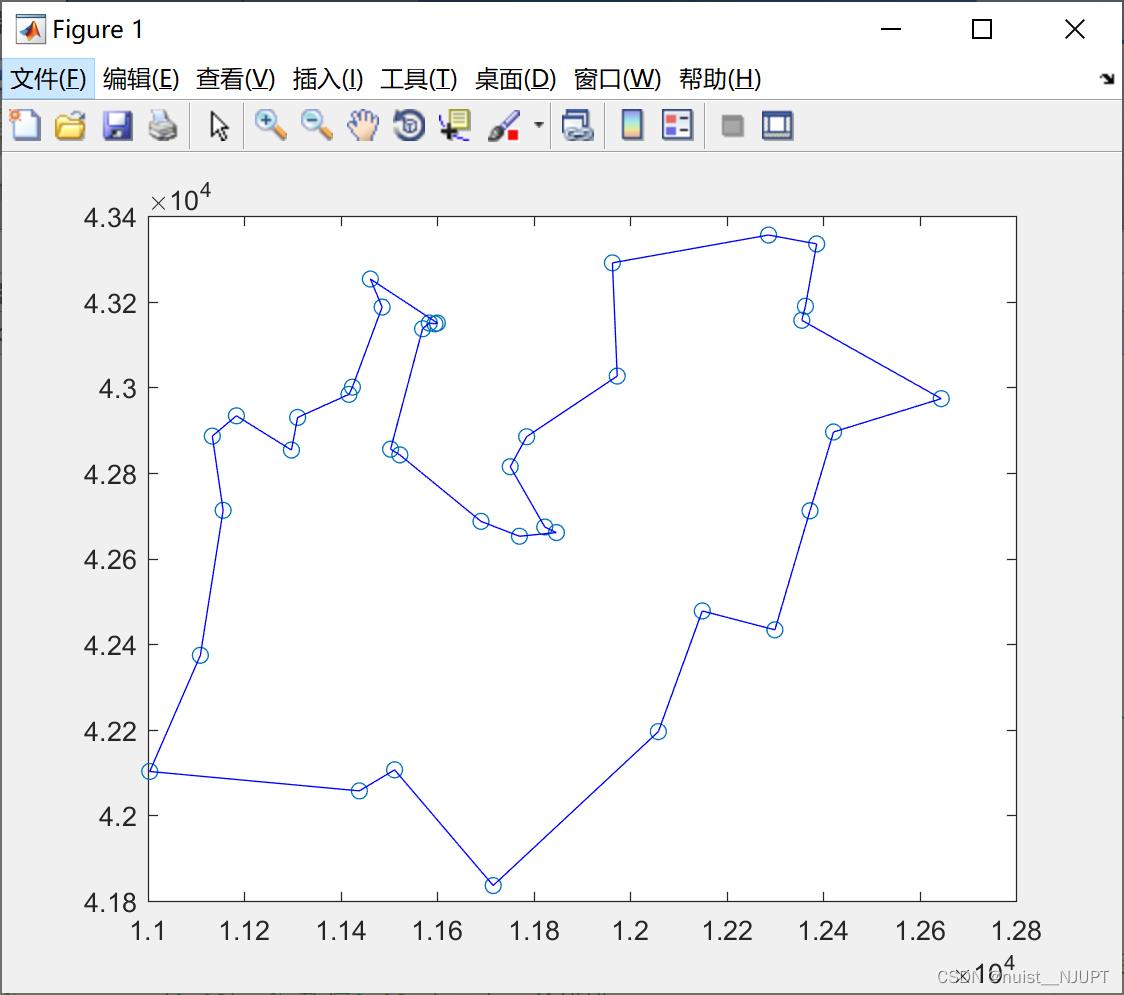
1.4、模拟退火求解组合优化问题
下面我们看一下书店买书问题，之前使用的蒙特卡洛模拟的方法进行求解书店买书问题，现在我们增加商城和书的数量，使用模拟退火来解决这个问题。
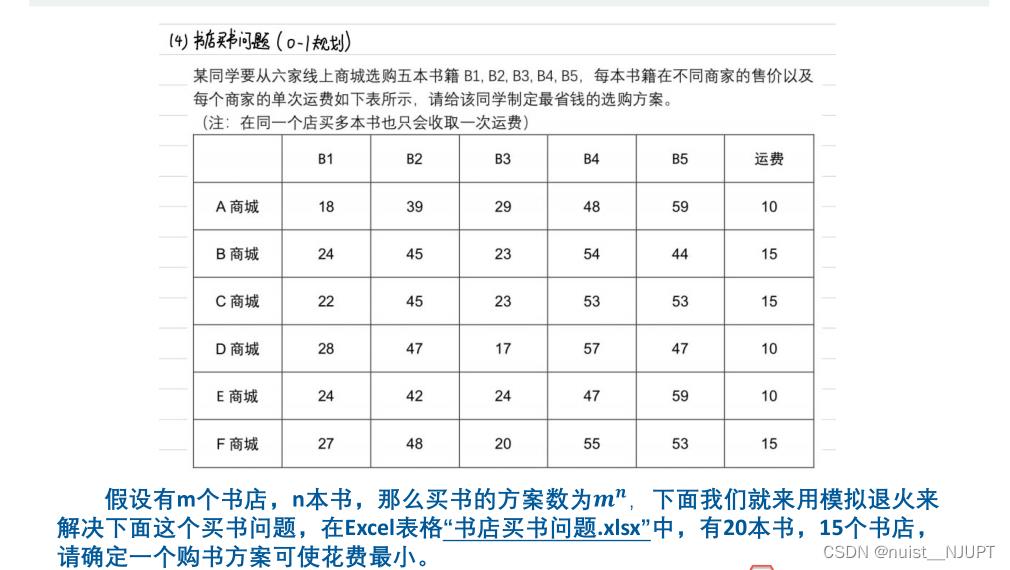
书店买书问题：在5家书店买20本书的例题，使用模拟退火算法求解，通过改变书购买的书店生成新的解，如果目标函数值小，则更新新的解，否则按概率接受新的解。
模拟退火求解书店买书问题的代码如下：
%% 模拟退火解决书店买书问题 % 466
tic
rng('shuffle') % 控制随机数的生成，否则每次打开matlab得到的结果都一样
load book_data % 这个文件一定要在当前文件夹下面
% 这个数据文件里面保存了两个矩阵：M是每本书在每家店的价格; freight表示每家店的运费
[s, b] = size(M); % s是书店的数量，b是要购买的书的数量
%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 500; % 最大迭代次数
Lk = 200; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
%% 随机生成一个初始解
way0 = randi([1, s],1,b); % 在1-s这些整数中随机抽取一个1*b的向量，表示这b本书分别在哪家书店购买
money0 = calculate_money(way0,freight,M,b); % 调用我们自己写的calculate_money函数计算这个方案的花费
%% 定义一些保存中间过程的量，方便输出结果和画图
min_money = money0; % 初始化找到的最佳的解对应的花费为money0
MONEY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_money (方便画图）
%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数
for i = 1 : Lk % 内循环，在每个温度下开始迭代
way1 = gen_new_way(way0,s,b); % 调用我们自己写的gen_new_way函数生成新的方案
money1 = calculate_money(way1,freight,M,b); % 计算新方案的花费
if money1 < money0 % 如果新方案的花费小于当前方案的花费
way0 = way1; % 更新当前方案为新方案
money0 = money1;
else
p = exp(-(money1 - money0)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
way0 = way1;
money0 = money1;
end
end
% 判断是否要更新找到的最佳的解
if money0 < min_money % 如果当前解更好，则对其进行更新
min_money = money0; % 更新最小的花费
best_way = way0; % 更新找到的最佳方案
end
end
MONEY(iter) = min_money; % 保存本轮外循环结束后找到的最小花费
T = alfa*T; % 温度下降
end
disp('最佳的方案是：'); disp(mat2str(best_way))
disp('此时最优值是：'); disp(min_money)
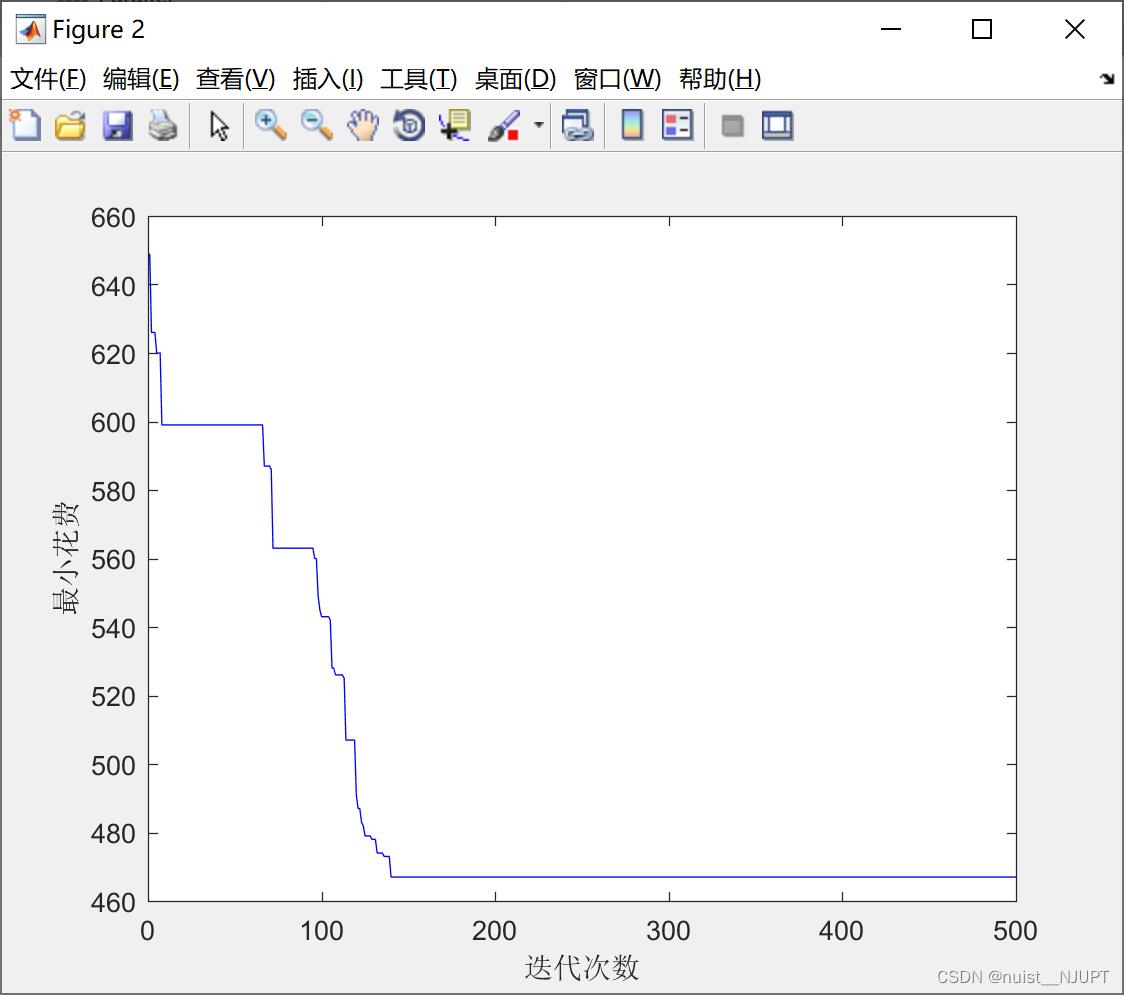
%% 画出每次迭代后找到的最佳方案的图形
figure
plot(1:maxgen,MONEY,'b-');
xlabel('迭代次数');
ylabel('最小花费');
toc得到新的购书方案的方法，即新的解。
function way1 = gen_new_way(way0, s, b)
% way0：原来的买书方案，是一个1*b的向量，每一个元素都位于1-s之间
index = randi([1, b],1) ; % 看哪一本书要更换书店购买
way1 = way0; % 将原来的方案赋值给way1
way1(index) = randi([1, s],1); % 将way1中的第index本书换一个书店购买
end
计算总的费用的方法：
function money = calculate_money(way,freight,M,b)
% 输入：way: 购买方案； fright:运费; M: 每本书在每家店的价格; b：一共要购买几本书
index = unique(way); % 在哪些商店购买了商品，因为我们等下要计算运费
money = sum(freight(index)); % 计算买书花费的运费
% 计算总花费：刚刚计算出来的运费 + 五本书的售价
for i = 1:b
money = money + M(way(i),i);
end
end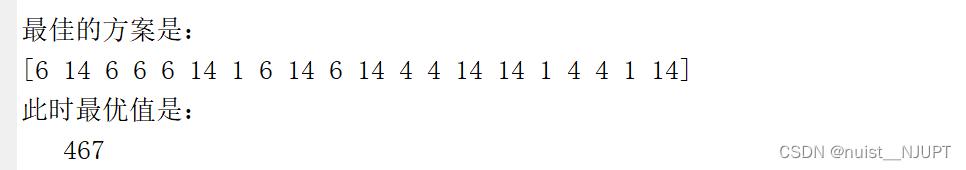
以上是关于备战数学建模45-模拟退火算法SA(攻坚站9)的主要内容，如果未能解决你的问题，请参考以下文章