递归算法深入浅出五:深度搜索寻找图最短路径
Posted 老猫烧须
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了递归算法深入浅出五:深度搜索寻找图最短路径相关的知识,希望对你有一定的参考价值。
版权声明
如果你看到这篇文章并不是在我的CSDN博客发布,同时文章里面的图片、URL全没了的,那么,很有可能你上了一个爬虫网站!
在此,我建议你马上关闭该页面!因为爬虫或多或少都会出现内容的纰漏,对读者造成的危害更大,误人子弟。
同时,转载本文的请加上本文链接:http://blog.csdn.net/nthack5730/article/details/71774434
对于爬虫网站随意爬取以及转载不加本文链接的,本人保留追究法律责任的权力!
对于不尊重版权的行为,我们也没必要客气!
递归算法概述及常见算法列表,传送门:
http://blog.csdn.net/nthack5730/article/details/65537530
深度优先搜索
又称深度搜索、深搜。简单地说深搜就是一种**【不撞南墙不回头】** 的 暴力算法,基本上该算法常用递归作为设计基础,当然也有使用for循环嵌套的,本文是以递归为讲解方向的。
至于更深一层的理论在这里就不详细说明了,详细可以去搜索更多关于。
简单的图搜索问题
本文讲述的是一个基于无向图为基础的图搜索,用二位数组组成的图。
【关于图的更多的理论也麻烦大家去搜索相关的资料,今天写这个文章主要针对下面描述的问题,在这里不过多阐述】
问题描述
描述如下:
在一个n行m列组成的二位数组中,每个单元格代表空地或障碍物。
邻接的单元格距离单位为1,但不包括对角的单元格。
图中是属于无向图,移动的方向不受限制(不能出界)。
现在给定在图中任意的两个坐标(两个均坐标不属于障碍物),求出两个坐标之间到达的最短距离。
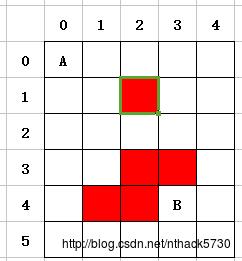
如图:
这是一个6行5列的图,其中 (1,2)、(3,2)、(3,3) 、(4,1)、(4,2) 为障碍物
求A点到B点的最短距离
问题分析
问题中可以知道这是一个由二维数组组成的图,每个单元格代表空地或者障碍物。
现在要从A点到达B点或者从B点到达A点,行走的方向可以是(上、下、左、右),同时要避开所有红色的障碍物(如上图)。首先要明白每走一步所到达的位置:
- 当在A点(0,0)时,下一步能到达的点为**(0,1)、(1,0)**
- 当在点**(0,1)时,下一步能到达的点为(0,0)、(1,1)、(1、2)**
- 当在点**(1,0)时,下一步能到达的点为(0,0)、(2,0)、(1、1)**
- 当在点**(1,1)时,由于(1,2)为障碍物**,因此下一步能到达的点为**(0,1)、(1,0)、(2,1)**
- 每一步都去尝试下一步可以到达的位置,直到到达终点B。
有个问题就来了,例如上面的,有的位置是已经被走过的,如果程序没有对走过的位置进行判断,那么可能永远都不能到达B点...
应该怎么做呢?定义一个结果集来记录当前访问过的点。
请慢慢往下看,别急!
递归程序设计思路
一、定义
1. 设定地图
我们可以用一个二维的 int 数组来表示该图,我们假设在数组中:- 值为 1 的是障碍物
- 值为 0 的是为空地
- 注意:使用二维int数组的原因是:如果需要,可以用数字表示不同类型的障碍物,本问题中可以用boolean数组表示空地或障碍物,但为了让大家更加清晰不和下面的 boolean[][] used 二维标记数组弄混,还是使用 int[][] map 来定义。
那么就可以得出下列二维数组:
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 1 1 0
0 1 1 0 0
0 0 0 0 0
2. 首先是定义需要用上的变量:
- int n,m:定义图的大小。
- int[][] map:需要搜寻的图(在这里用int[][]二维数组表示)
- boolean[][] used:大小和图一样,用于标记被访问过的点(访问过为true),保证每次走的都是没有被走过的点,这也是解决上面的重复访问同一个点的问题的方案
- int p,q:终点的Y轴、X轴坐标,由用户输入。
- int count:计算由起点到终点所有的可行路径。
- int minStep:记录最短路径所需要的步数,因为要考虑起点和终点为同一个点,因此设定初始值为 -1。
3.设定一个 dfsMap(...) 方法,该方法主要用于深度搜索图。
除了上面设定的变量,dfsMap(...) 需要管理的参数有:- int x:当前点所在的X轴坐标值
- int y:当前点所在的Y轴坐标值
- int step:当前点与开始点的距离
此文老猫原创,转载请加本文连接:http://blog.csdn.net/nthack5730/article/details/71774434
更多有关老猫的文章:http://blog.csdn.net/nthack5730
二、代码编写的思路
当我们在一个点时,需要做的是要判断当前所在的点是否为终点,如果是终点,那么就对历史记录进行判断,代码如下:
if (y == p && x == q)
System.out.println("找到一条路径,距离为:" + step);
count++;
if (minStep == -1)
minStep = step;
if (step < minStep)
minStep = step;
如果不是终点,那么程序就要去寻找当前点的下一步;同时,我们需要用上boolean[][] used二维数组,大小和当前的地图一样,用于标记当前地图中哪些点被访问过,如果被访问过,那么就跳过该点。
假设目前所在点的位置为 (x,y),那么可以得出下一步可到达的点为:
(x+1, y)、(x-1, y)、(x, y+1)、(x, y-1),如下图:
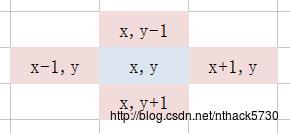
转换成代码形式就是,该数组可以定义为全局静态变量:
int[][] wayPoint = 0, 1, 0, -1, 1, 0, -1, 0;
根据上面四个点,用表格来表示(X,Y)坐标的变化量更为直观:(以行为变化单位)
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
用循环就能得到以(X,Y)为中心的周边四个点。
但得出这些点并不能一下子就进行递归寻路操作,要确定这些点是不是能够“走”得到,需要对其进行边界和障碍物以及该点是否被访问过判断。代码如下:
for (int i = 0; i < 4; i++)
int gX, gY;//新的坐标位置
gX = x + wayPoint[i][0];//获取每行的第0列,即上面表格中X的变化值
gY = y + wayPoint[i][1];//获取每行的第1列,即上面表格中Y 的变化值
//判断越界
if (gX < 0 || gX >= m || gY < 0 || gY >= n)
continue;
//判断障碍物,以及该点是否被访问过
if (map[gY][gX] == 1 || used[gY][gX] == true)
continue;
....
三、得到dfs(...)递归体代码
在对新的点进行判断后,就确定该点是能到达的,那么就可以 将当前的结果集(即当前深度搜索所走过的位置的集合) 进行递归,继续交给 dfsMap(...) 方法进行迭代寻找。
在进入该点之前,我们需要标记该点已经被访问过,同时在递归结束之后要对标记进行消除, dsfMap(int, int ,int) 核心代码如下:
/**
* @param x 当前所处的X轴坐标
* @param y 当前所处的Y轴坐标
* @param step 距离
*/
static void dfsMap(int x, int y, int step)
if (y == p && x == q)
//System.out.println("找到一条路径,距离为:" + step);
count++;
if (minStep == -1)
minStep = step;
if (step < minStep)
minStep = step;
else
for (int i = 0; i < 4; i++)
int gX, gY;//新的坐标位置
gX = x + wayPoint[i][0];//获取每行的第0列,即上面表格中X的变化值
gY = y + wayPoint[i][1];//获取每行的第1列,即上面表格中Y 的变化值
//判断越界
if (gX < 0 || gX >= m || gY < 0 || gY >= n)
continue;
//判断障碍物,以及该点是否被访问过
if (map[gY][gX] == 1 || used[gY][gX] == true)
continue;
used[gY][gX] = true;
dfsMap(gX, gY, step + 1);
used[gY][gX] = false;
此文老猫原创,转载请加本文连接:http://blog.csdn.net/nthack5730/article/details/71774434
更多有关老猫的文章:http://blog.csdn.net/nthack5730
测试
最终完整的代码如下:
//此文老猫原创,转载请加本文连接:
//http://blog.csdn.net/nthack5730/article/details/71774434
//更多有关老猫的文章:http://blog.csdn.net/nthack5730
public class SearchMap
static int[][] map;
static boolean[][] used;
//图面积设置
static int n;
static int m;
//需要寻找的点
static int p;
static int q;
//最小位置
static int minStep = -1;
//次数统计
static int count = 0;
static int[][] wayPoint = 0, 1, 0, -1, 1, 0, -1, 0;
public static void main(String[] args)
Scanner scan = new Scanner(System.in);
System.out.println("输入图的行、列:");
n =scan.nextInt();
m =scan.nextInt();
System.out.println("输入开始点的坐标:");
int startX = scan.nextInt();
int startY = scan.nextInt();
System.out.println("输入终点的坐标:");
p =scan.nextInt();
q =scan.nextInt();
map = new int[n][m];
used = new boolean[n][m];
System.out.println("输入图数据:");
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
map[i][j] = scan.nextInt();
//递归调用开始
used[startY][startX] = true;//初始化开始点被访问过,注意Y值代表行,X值代表列
dfsMap(startX, startY, 0);
//输出结果
System.out.println("\\n//=============================");
System.out.println("// 找到的总路径数为:" + count);
if (minStep == -1)
System.out.println("// 没有找到结果");
else
System.out.println("// 最小距离为:" + minStep);
System.out.println("\\n//=============================");
/**
* 深搜暴力寻图
*
* @param x 当前所处的X轴坐标
* @param y 当前所处的Y轴坐标
* @param step 距离
*/
static void dfsMap(int x, int y, int step)
if (y == p && x == q)
// System.out.println("找到一条路径,距离为:" + step);
count++;
if (minStep == -1)
minStep = step;
if (step < minStep)
minStep = step;
else
for (int i = 0; i < 4; i++)
int gX, gY;//新的坐标位置
gX = x + wayPoint[i][0];//获取每行的第0列,即上面表格中X的变化值
gY = y + wayPoint[i][1];//获取每行的第1列,即上面表格中Y 的变化值
//判断越界
if (gX < 0 || gX >= m || gY < 0 || gY >= n)
continue;
//判断障碍物,以及该点是否被访问过
if (map[gY][gX] == 1 || used[gY][gX] == true)
continue;
used[gY][gX] = true;
dfsMap(gX, gY, step + 1);
used[gY][gX] = false;
测试输入如下:
输入图的行、列:
6 5
输入开始点的坐标:
0 0
输入终点的坐标:
4 3
输入图数据:
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 1 1 0
0 1 1 0 0
0 0 0 0 0
程序输出:
//=============================
// 找到的总路径数为:124
// 最小距离为:9
//=============================
总结
难点所在
至此,深度搜索图的最短路径已经完成。其中最难理解的应该就是每次递归前标记位置已经被访问,并且在递归结束(相当于当前层)后对标记进行撤销:
....
used[gY][gX] = true;
dfsMap(gX, gY, step + 1);
used[gY][gX] = false;
....
回到图搜索
我们将图分为两类结果集:
- 一类是“已经被访问过的”结果集
- 剩下的就是“没有被访问过的”结果集
- 每次进行下一步都是以 当前“已经被访问过的”集合 为基础,将当前的结果集继续迭代
- 当 “当前的结果集” 所有的可能性都被尝试完时,就要将当前结果集的最后一步还原为上一个结果集的状态。
在这里,我简单地用数学集合表示法描述下:
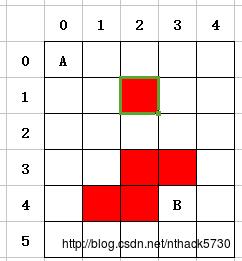
按照上图,假设程序在前面访问了2个点:(0,0)、(0,1),其中(0,1)是目前游标所在(最后一个访问的)。
设U为全图所有点的集合,设A为“已经被访问过的”结果集,当**A ={(0,0)、(0,1)}**时,剩下的 {U - A} 都是没有被访问的集合。
按照【每次只能走一步】的约定,当我们要走下一步时只能走(0,2)、(1,1)两个中的一个:
- 按照顺时针访问顺序,我们先走(0,2)这个点,对应代码中标记:
used[gY][gX] = true;
- 当走到(0,2)时,集合A就变为{(0,0),(0,1),(0,2)},设为A1,如果还要继续往下走,那么就要在A1的基础上继续扩展,对应代码中递归调用,表示继续从(0,2)这个点继续扩展其所有的结果:
dfsMap(gX, gY, step + 1);
- 当A1所有的情况都尝试完的时候,A1就要返回A的集合状态,这时就要从集合A1中移除(0,2),在代码中也就是取消(0,2)的标记:
used[gY][gX] = false;
- 当返回到集合A的数据时,就要去访问(1,1)这个点,继续重复上面的1,2,3步。
至于扩展的顺序,就是根据上面定义的方向数组waypoint数组,用for循环获取所有的(上、下、左、右)可能,然后进行1,2,3步
当然,在进行递归迭代之前,要对新的点进行边界、障碍物判断。
这个过程与全排列生成的解答树相似
图片参考《算法竞赛:入门经典》中P119页的图。
里面通过描述全排列生成的解答树,和本题的思维非常相似,如图:
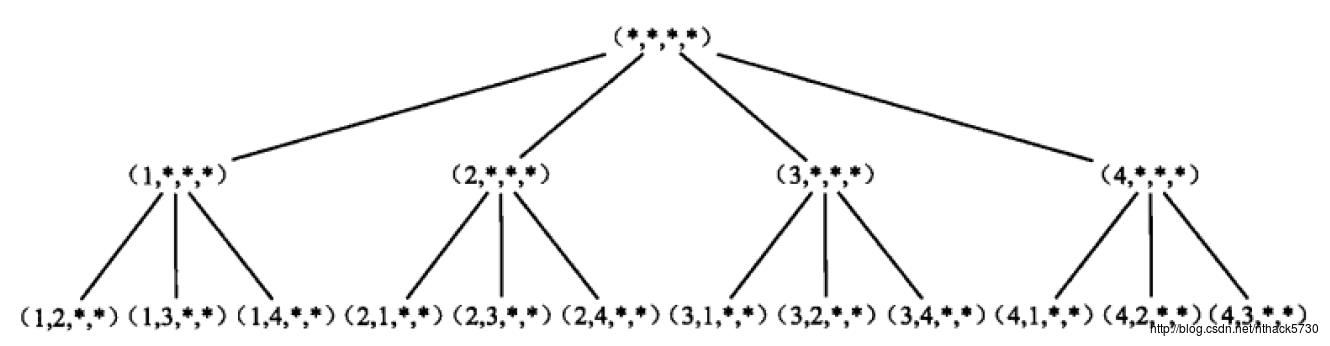
和全排列相似地,整个过程就如同生成一棵解答树【如图】:
- 每到达一个结点,所有已知的(走过的)都是一个结果集;
- 同时当前结果集与下一个可行的结点又会形成一个新的结果集(可行的结点越多,新的结果集越多);
- 如此下去,直到当前结果集的所有可行结点被列举,返回当前结果集的上一个结果集;
- 当所有的结果集都被列举,那么就能得出所有可行性的遍历。
写在最后
虽然本人技术和文笔和很多大牛相比都是一般般的,但我乐于和大家分享技术、交流。
撰写本文差不多花了一个多星期的时间去收集整理资料、写稿。代码也前后修改了很多次,不修改分块发出来很多人根本看不懂(变量比较多),也不想一次过全部代码“无脑推送”。如果你喜欢本文,请在下面给我点个赞吧!
(^ _ ^)
版权声明
如果你看到这篇文章并不是在我的CSDN博客发布,同时文章里面的图片、URL全没了的话,那么,很有可能你上了一个爬虫网站!
在此,我建议你马上关闭该页面!因为爬虫或多或少都会出现内容的纰漏,对读者造成的危害更大,误人子弟。
同时,转载本文的请加上本文链接:http://blog.csdn.net/nthack5730/article/details/71774434
对于爬虫网站随意爬取以及转载不加本文链接的,本人保留追究法律责任的权力!
对于不尊重版权的行为,我们也没必要客气!