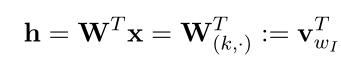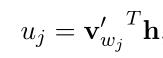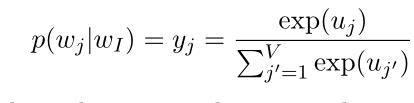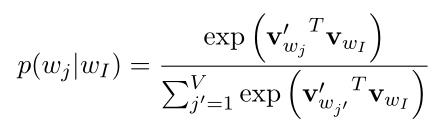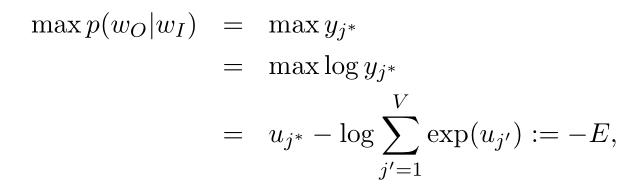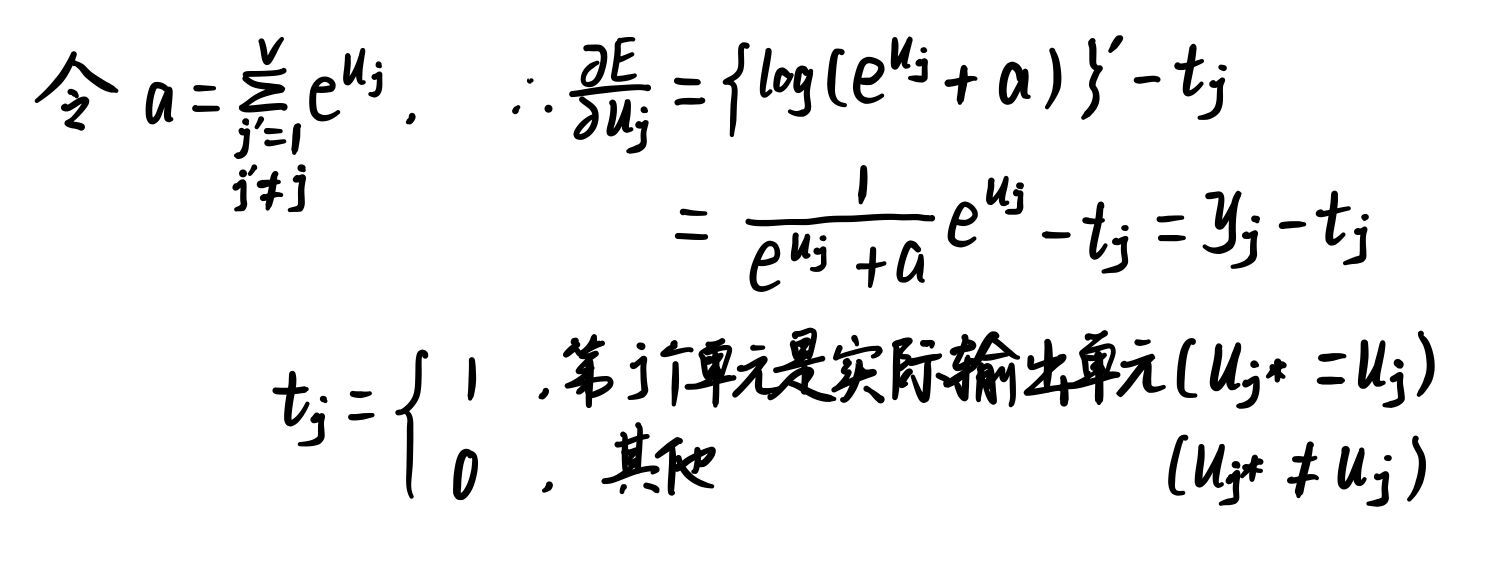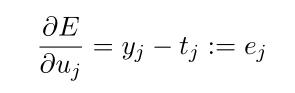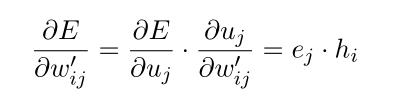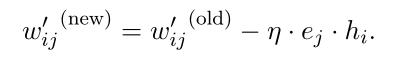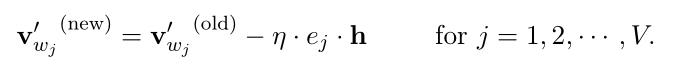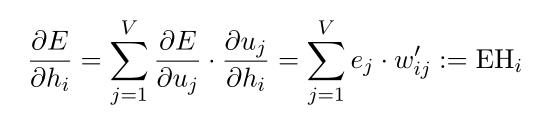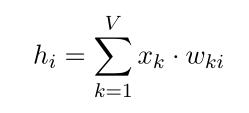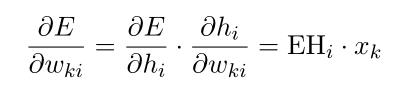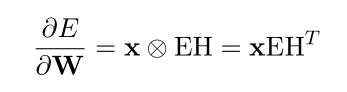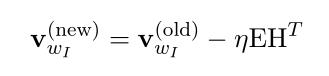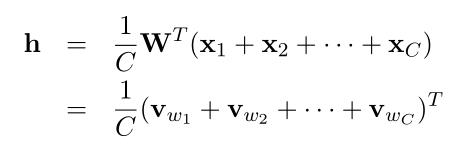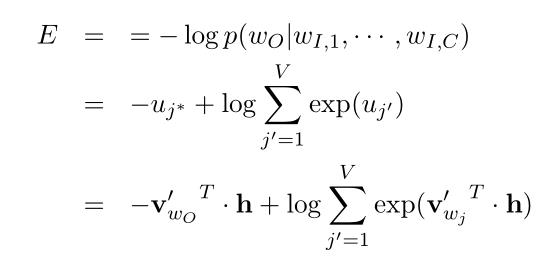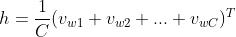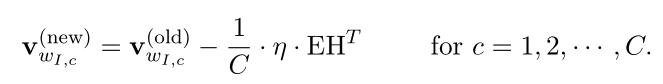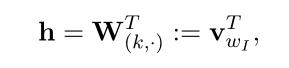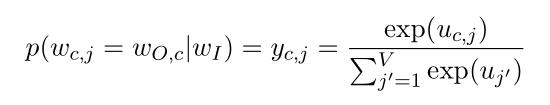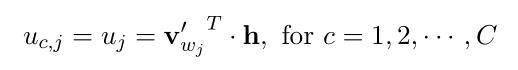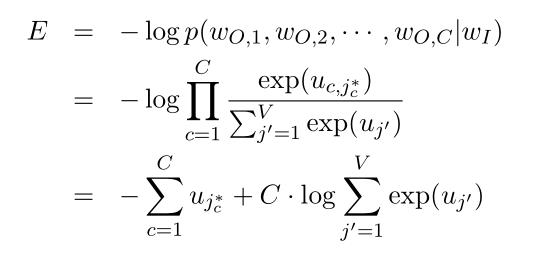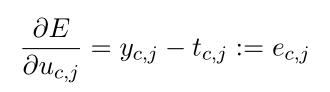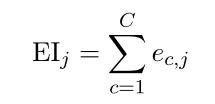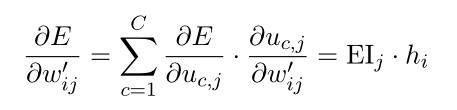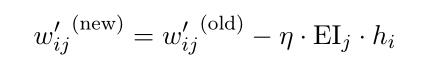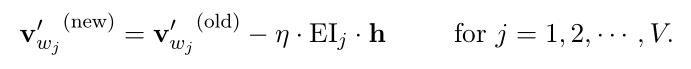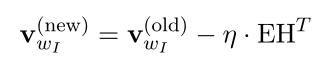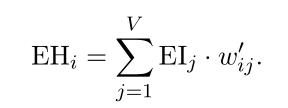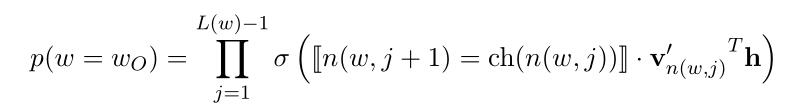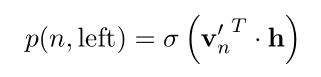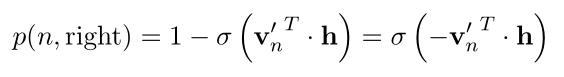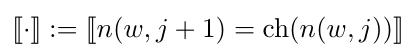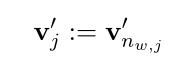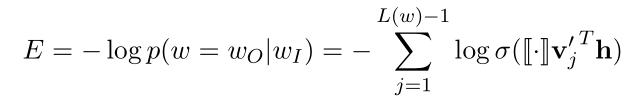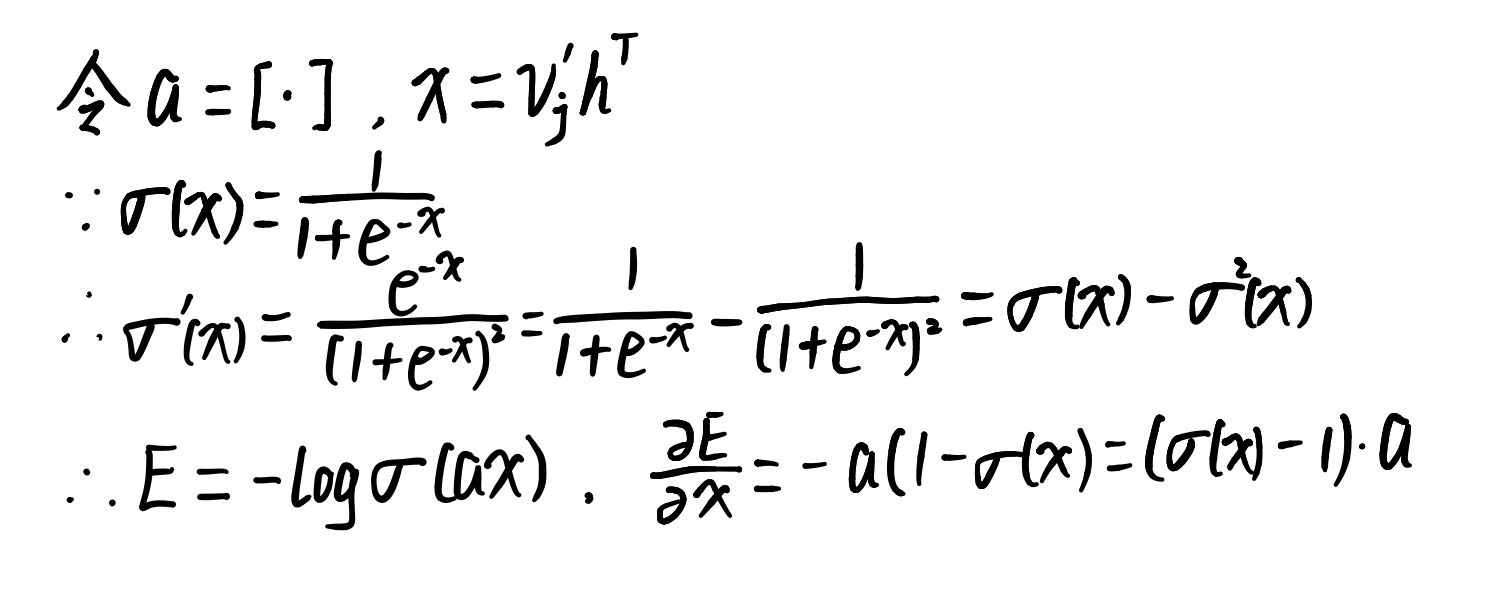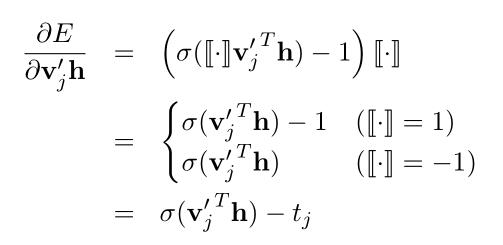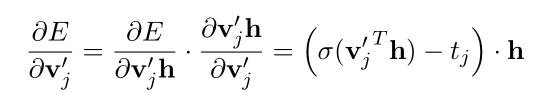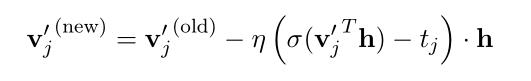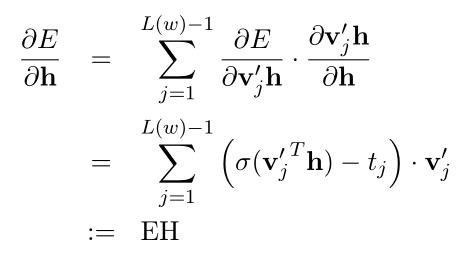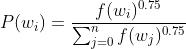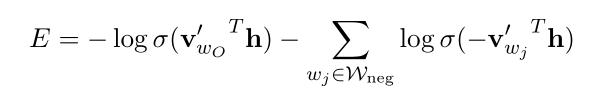word2vec
Posted 2016bits
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了word2vec相关的知识，希望对你有一定的参考价值。
目录
1. CBOW（Continuous Bag-of-Word Model）
1.1 根据一个上下文词预测目标单词（笔者为后续方便，将其简记为simple CBOW）
1. Hierarchical Softmax（分层softmax）
目前刚开始看斯坦福大学的cs224自然语言处理课，看到word2vec，一些细节部分不是太懂，所以参考https://arxiv.org/pdf/1411.2738.pdf，对word2vec的相关内容做了一点总结，欢迎读者对写的不好的地方进行指正。
一、模型提出背景及其核心思想
在自然语言处理过程中，处理的基本单位是单词（word），以往的机器学习处理的都是数值型的数据，所以需要将单词转化为数值型变量。如果将所有单词进行统计，形成一个维度为单词总数的向量，对任一单词，该单词向量对应位置为1，其余位置为0，这种单词表示形式为one-hot（独热表示）。
但one-hot这种表示方法一是因为存储开销过大，二是因为无法表示单词之间的相似关系。如：
motel [0 0 0 1 0 0 0 0 0 0 0 ... 0 0]
hotel [0 0 0 0 0 0 1 0 0 0 0 ... 0 0]
两者做点积，结果为0，但motel（汽车旅馆）与hotel（酒店）相似度还是挺高的，但one-hot无法表示这种相似性
于是word2vec考虑单词出现的上下文，并使用深度学习的方法来学习单词的向量表示。所以下面介绍两种模型框架，通过参数传递和反向传播进行参数更新，直至构建目标模型，最后将单词输入模型得到单词的向量表示。
两种模型框架：
- CBOW（Continuous Bag-of-Word Model）：根据上下文预测目标单词
- Skip-Gram Model：根据单词预测上下文
两种优化算法：
- Hierarchical Softmax：构建以将要更新的单词为根节点的哈夫曼树进行参数更新
- Negative Sampling：将输出单词作为positive sample，随机选择一部分词作为negative sample进行参数更新
二、模型框架
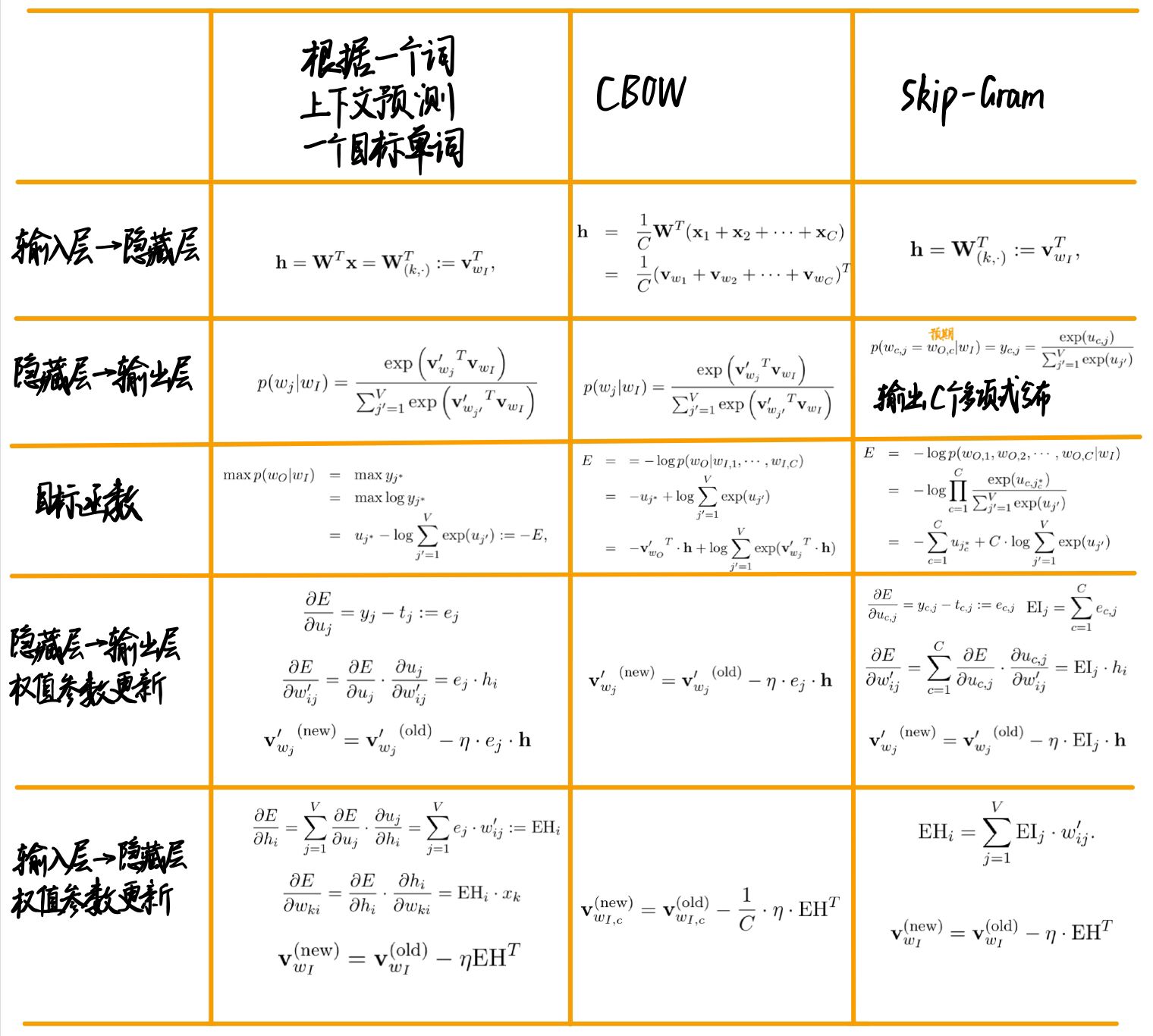
1. CBOW（Continuous Bag-of-Word Model）
1.1 根据一个上下文词预测目标单词（笔者为后续方便，将其简记为simple CBOW）
单词数量为V，隐藏层数量为N，神经元之间是全连接。输入为one-hot向量（因为会在学习过程中进行更新，所以初始值影响不大）。模型框架：（图2-1）
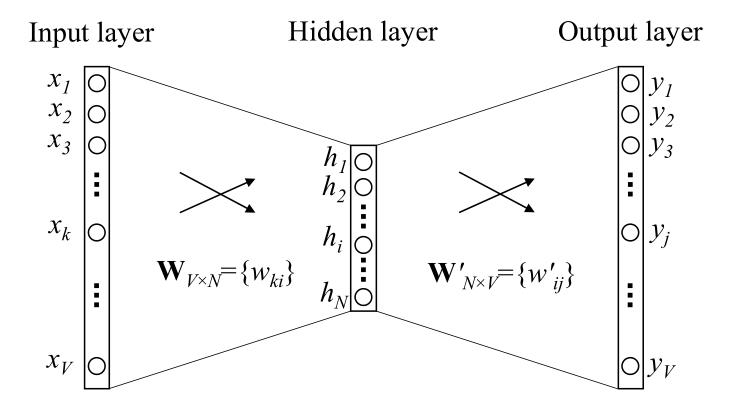
输入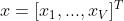
是one-hot向量，即只有一个位置为1，其余位置为0
输入层权值矩阵W为V×N型，W=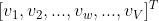
,
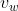为输入向量（输入层->隐藏层权值矩阵的行）的N维向量表示
输出层权值矩阵W'为N×V型，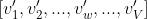
，
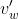为输出向量（隐藏层->输出层权值矩阵的列）的N维向量表示
隐藏层的激活函数单元是简单线性的，即：隐藏层输入的权值和能直接传递给下一层
输入层与隐藏层之间的关系：（式2-1）
词汇表中每个词的得分：（式2-2）
从隐藏层到输出层：使用softmax函数:（式2-3）
其中，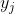
是输出层中第j个单元的输出，将（式2-1）和（式2-2）带入（式2-3）：
反向传播更新参数：
（1）隐藏层->输出层参数更新（权值矩阵W')：
求解目标为：在给定输入上下文向量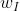
的条件下目标单词向量
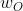的条件概率最大，即：（式2-4）
（式2-5）：
根据链式法则，计算隐藏层->输出层的权值梯度：（式2-6）
使用随机梯度下降法，得到隐藏层->输出层的权值更新公式：（式2-7）
向量形式：（式2-8）
分析式2-8：
当输出概率
时，则减去梯度；
当输出概率
如果输出概率
如果输出概率
（2）输入层->隐藏层参数更新（权值矩阵W）：
计算隐藏层的输出误差对隐藏层单元的偏导：（式2-9）
其中，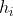
为隐藏层的第i个单元；
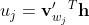，是输出层中dij个单元的输入；
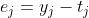，是输出层第j个单词的预测误差
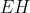是一个N元向量，EH = 
因为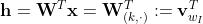
，所以（式2-10）
使用链式法则：（式2-11）
向量形式：（式2-12）
因为x只有一个非零值，所以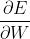
中只有一行是非零的
使用梯度下降法，得到参数更新公式：（式2-13）
W中只有输入向量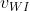
这一行非零，只有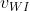得到更新，其余不变
1.2 根据多个上下文词预测目标词（记为CBOW）
与simple CBOW相比，不同点：计算隐藏层的输出时，取上下文单词输入向量的平均，用其与（输入层->隐藏层权值矩阵W）的乘积作输出
框架图：（图2-2）
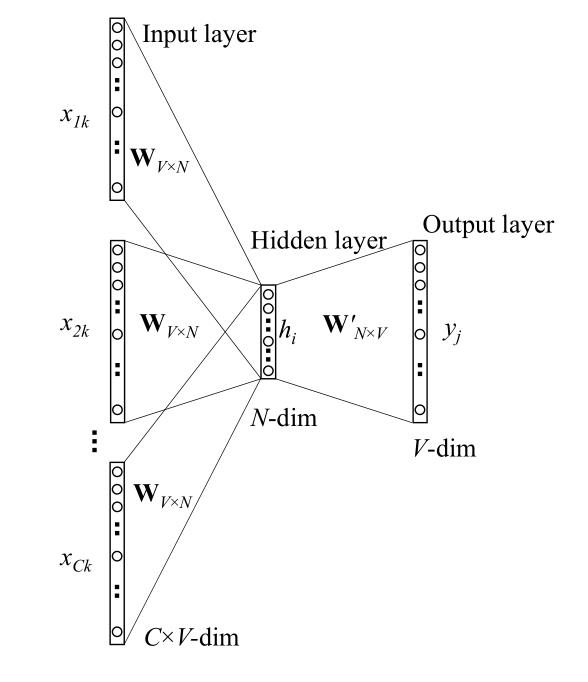
计算隐藏层的输出：（式2-14）
其中，C是上下文单词数量
损失函数：（式2-15）
式2-15同simple CBOW的式2-4。两者的不同在于：
simple CBOW：输入隐藏层中的向量只有一个
CBOW：输入隐藏层中的向量是多个向量的平均
反向传播参数更新：
同simple CBOW的情况（同式2-8）：（式2-15）
拓展到向量矩阵形式：（式2-16）
注意此处与simple CBOW（式2-13）的不同：
因为在simple CBOW中，权值矩阵W中只有输入向量
这一行非零
在CBOW中，权值矩阵W的C行输入向量均非零，所以需要取平均
2. Skip-Gram Model（简记为SG）
在Skip-Gram Model中，目标词在输入层，上下文单词在输出层。在隐藏层->输出层中，使用softmax函数，计算在目标单词条件下产生的上下文单词的概率，然后取概率最高的C个单词作为结果。
框架图：（图2-3）
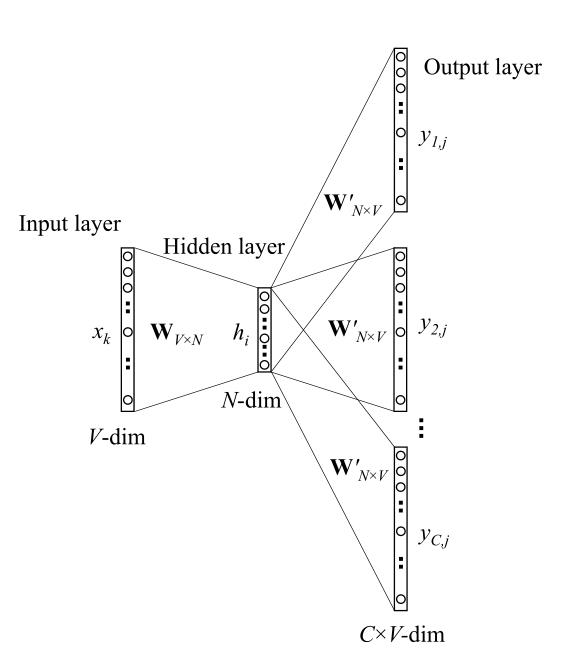
相比于simple CBOW，SG的输入也是一个单词，所以输入部分同式2-1：（式2-14）
因为隐藏层的输入只有一个单词，所以计算隐藏层->输出层的输出时，均共享一个权值矩阵：（式2-15）
SG模型的输出是多个上下文单词，所以相比于simple CBOW输出一个多项式分布，SG输出的是C个多项式分布
在式2-15中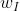，是唯一的输入单词，由于最终要输出C个多项式分布，所以考虑输出的第c个单词（c=1,2,...,C）：
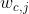表示输出层的第j的单词，
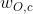表示预期得到的单词，第j个单词的得分：（式2-16）
其中，输出的第j个单词的输出向量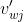
：来自隐藏层->输出层权值矩阵W'的某一列
因为输出了C个上下文单词的分布，所以使用最大似然估计求它们预测概率乘积的最大值：（式2-17）
更新隐藏层->输出层的权值：
求导：（式2-18）
为了表示简单，使用一个V维向量表示所有上下文单词的预测误差和：（式2-19）
使用链式法则，考虑隐藏层->输出层的权值矩阵W'：（式2-20）
于是得到隐藏层->输出层权值矩阵W'的参数更新方程：（式2-21）
向量形式：（式2-22）
式2-22与simple CBOW的式2-8类似，不同在于SG中的预测误差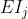
是C个上下文单词的预测误差的和
由于SG的输入只有一个单词，所以更新输入层->隐藏层权值时公式与simple CBOW的式2-13类似：（式2-23）
不同在于SG的将预测误差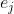
用误差和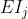替换：（式2-24）
三、优化算法
在更新输出向量的过程中，每次迭代都需要计算所有词的预测值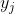和预测误差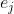，导致计算量过大，所以尝试对其进行优化。
直觉上的改进方法：限制每次训练时必须更新的输出向量数目。下面主要介绍两种优化算法：
1. Hierarchical Softmax（分层softmax）
基本思想：
原：更新一个词向量时，需要计算所有词的softmax概率，然后选择概率最大的
Hierarchical Softmax：更新一个词向量时，只需要沿着以该词为根节点的哈夫曼树进行更新
Hierarchical Softmax将之前的多分类转化为多个二分类的组合
该算法将词汇表中的所有词用一棵二叉树表示
叶结点表示V个单词
叶结点到根节点的唯一路径表示预测单词概率
n(w,j)表示从根节点到单词w的路径上的第j个单元
该二叉树含有V-1个非叶子节点（内节点inner units）。该模型中没有单词的输出向量表示，但是V-1个非叶子节点均有一个输出向量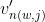
一个单词作为输出单词的概率为：（式3-1）
其中，ch(n(w,j))表示单元n(w,j)的左孩子节点，[n(w, j+1) = ch(n(w,j))]用于判断n(w,j)的左孩子节点是否为n(w, j+1)，若是，则该式为1；若不是，则为-1.简单来说，即判断从节点n(w,j)向下走时，是否向左走，如果向左走，则该值为1；若向右走，则该值为-1.
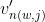表示内节点n(w,j)的输出向量表示，h表示隐藏层中的输出值（在SG中，
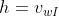；在CBOW中，
)
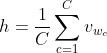因为是二分类，所以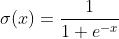
为sigmoid函数，且有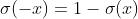
定义节点n向左走的概率：（式3-2）
向右走的概率：（式3-3）
示意图：（图3-1）
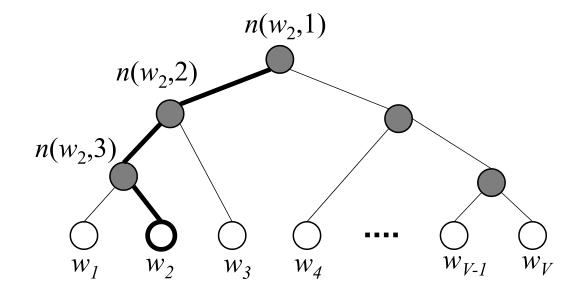
图中，白色节点表示词汇表中的单词，黑色节点表示内单元（inner units），图中一条从根节点到
的路径被加粗了。
所以图中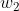是输出单词的概率为：（式3-4）
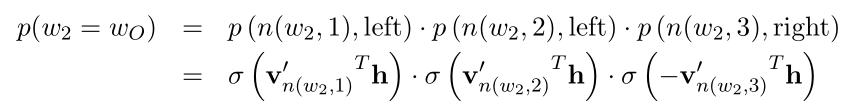
下面将该算法具体应用于simple CBOW：
首先对符号进行简化：（式3-5、式3-6）
在训练中，损失函数为：（式3-7）
在求导前先进行简化计算：
所以有：（式3-8）
当[·]=1时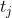，=1；当[·]=-1时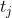，=0
使用链式法则：（式3-9）
得到参数更新方程：（式3-10）
其中，j = 1, 2, ..., L(w)-1.
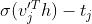用于预测内节点n(w,j)的误差。内节点的任务：在随机向叶结点移动时预测向左走还是向右走，当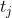=1时，向左走；当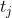=0时，向右走
在输入层->隐藏层的权值进行反向传播的过程中，有：（式3-11）
在CBOW中，式3-11可以直接带入式2-16：
在SG中，需要计算每个上下文单词的EH，然后求和，再将结果带入式2-23：
通过使用Hierarchical Softmax，可以将每次训练上下文单词的时间复杂度由O(V)降为O(log(V))，速度得到很大的提升。
2. Negative Sampling（负采样）
基本思想：
将输出单词作为正类，将采样得到的单词作负类，每次更新权重时只需要更新这些选中的词所对应的权重，可以极大提升速度。
在采样负类单词时，是通过随机选择一个概率分布来实现的，这个概率和单词出现的频率有关，更常出现的单词，更容易被选为负类。这个概率公式为：（式3-12）
其中，超参0.75是试出来的，这个函数的表现比其他函数的好。
所以改进后的目标函数也发生了改变：（式3-13）
改进前是对所有单词求损失和，改进后是对输出单词和采样的负类单词（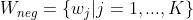
是在分布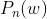
上采样得到的单词）求损失和
其余部分：计算梯度、反向传播更新参数均是针对采样单词，所以公式和改进前类似。
四、总结
Word2vec实际上有两种含义：
一是指将单词表示成向量形式；
二是指每个单词有两种向量表示形式（输入向量v和输出向量v’)，也就是作为当前单词和作为上下文单词的两种表示
输入向量和输出向量不同可以减少耦合，模型更容易设计；而且不至于将自身预测为当前词的上下文
模型构建的基本过程为：
首先输入one-hot表示的单词向量，然后经过输入层->隐藏层的权值矩阵W；接下来将隐藏层单元和输出向量作内积，求相似性，得到该单词的得分，再通过softmax函数求在该上下文条件（输入）下出现该单词（输出）的概率。最后分别计算隐藏层->输出层、输入层->隐藏层的梯度，并使用反向传播来更新参数。
三个模型公式对比：
改进算法的损失函数：
Hierarchical Softmax：
Negative Sampling：
以上是关于word2vec的主要内容，如果未能解决你的问题，请参考以下文章