Matlab数学建模TOPSIS(优劣解距离法)
Posted 九死九歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Matlab数学建模TOPSIS(优劣解距离法)相关的知识,希望对你有一定的参考价值。
一、问题引入
先分析一下层次分析法的不足。
① 平均随机一致性指标RI的表格中,n最大为15。那么n太大的话,无法进行一致性检验。

② 如果决策层中指标的数据是已知的,那么我们如何利用这些数据来使得评价的更加准确呢?
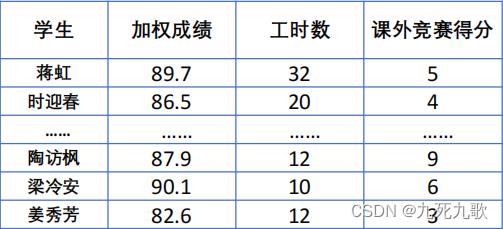
二、极大型指标构造计算评分
① 第一步:求最大最小值。
② 第二步:带入构造计算评分的公式 x − m i n m a x − m i n \\fracx - minmax - min max−minx−min。
③ 第三步:进行归一化。
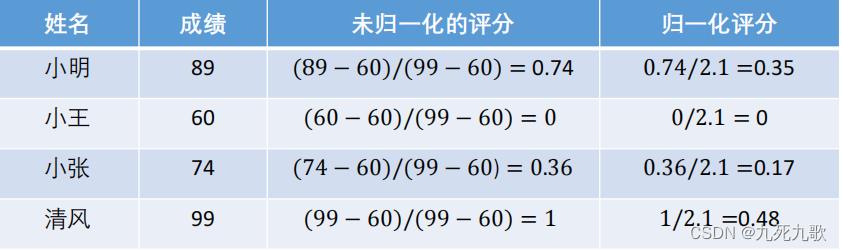
代码演示:
function res = func(a)
mnmx = minmax(a);
res = (a - mnmx(1)) / (mnmx(2) - mnmx(1));
res = res / sum(res);
end
(注:上面的评分规则是不正确的,只是用来抛砖引玉,正确的评分规则见下文“三、标准化”)
但是有时候评分不是越大越好,而是越小越好,或者越接近某个值越好,越接近某个区间越好。那就要把这些指标转换成极大型。这个过程叫做正向化。
但是不同指标的量纲是不一样的,为了消除量纲带来的影响,我们需要进行标准化。
下面先介绍标准化,在介绍正向化。
三、标准化
例如对于m个要评价的对象,n个评价指标的正向化矩阵:
X
=
(
x
11
x
12
⋯
x
1
n
x
21
x
22
⋯
x
2
n
⋮
⋮
⋱
⋮
x
m
1
x
m
2
⋯
x
m
n
)
X = \\beginpmatrix x_11 & x_12 & \\cdots & x_1n\\\\ x_21 & x_22 & \\cdots & x_2n\\\\ \\vdots & \\vdots & \\ddots & \\vdots\\\\ x_m1 & x_m2 & \\cdots & x_mn \\endpmatrix
X=⎝⎜⎜⎜⎛x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1nx2n⋮xmn⎠⎟⎟⎟⎞
将标准化后的矩阵记作Z,则Z中的每一个元素满足:
z
i
j
=
x
i
j
∑
i
=
1
m
x
i
j
2
z_ij = \\fracx_ij\\sqrt\\sum\\limits^m_i=1x^2_ij
zij=i=1∑mxij2xij
用代码描述为:
function Z = func(X)
[m, ~] = size(X);
Z = X ./ repmat(sum(X .^ 2) .^ 0.5, m, 1);
end
接下来对标准化矩阵求解各指标得分:
Z
=
(
z
11
z
12
⋯
z
1
n
z
21
z
22
⋯
z
2
n
⋮
⋮
⋱
⋮
z
m
1
z
m
2
⋯
z
m
n
)
Z = \\beginpmatrix z_11 & z_12 & \\cdots & z_1n\\\\ z_21 & z_22 & \\cdots & z_2n\\\\ \\vdots & \\vdots & \\ddots & \\vdots\\\\ z_m1 & z_m2 & \\cdots & z_mn \\endpmatrix\\\\
Z=⎝⎜⎜⎜⎛z11z21⋮zm1z12z22⋮zm2⋯⋯⋱⋯z1nz2n⋮zmn⎠⎟⎟⎟⎞
令
Z
j
+
=
max
(
z
1
j
,
z
2
j
,
⋯
,
z
m
j
)
Z
j
−
=
min
(
z
1
j
,
z
2
j
,
⋯
.
z
m
j
)
令Z^+_j = \\max(z_1j, z_2j, \\cdots, z_mj)\\\\ Z^-_j = \\min(z_1j, z_2j, \\cdots. z_mj)\\\\
令Zj+=max(z1j,z2j,⋯,zmj)Zj−=min(z1j,z2j,⋯.zmj)
D
+
=
(
Z
1
+
,
Z
2
+
,
⋯
,
Z
j
+
)
D
−
=
(
Z
1
−
,
Z
2
−
,
⋯
,
Z
j
−
)
D^+ = (Z^+_1, Z^+_2, \\cdots, Z^+_j)\\\\ D^- = (Z^-_1, Z^-_2, \\cdots, Z^-_j)\\\\
D+=(Z1+,Z2+,⋯,Zj+)D−=(Z1−,Z2−,⋯,Z