论文|LINE算法原理代码实战和应用
Posted 搜索与推荐Wiki
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文|LINE算法原理代码实战和应用相关的知识,希望对你有一定的参考价值。
1 概述
LINE是2015年微软发表的一篇论文,其全称为: Large-scale Information Network Embedding。论文下载地址:https://arxiv.org/pdf/1503.03578.pdf
LINE是一种基于graph产生embedding的方法,它可以适用于任何类型的graph,如无向图、有向图、加权图等,同时作者基于边采样进行了目标函数的优化,使算法既能捕获到局部的网络结构,也能捕获到全局的网络结构。
2 算法原理
2.1 新的相似度定义
该算法同时优化了节点的相似度计算方法,提出了一二阶相似度。
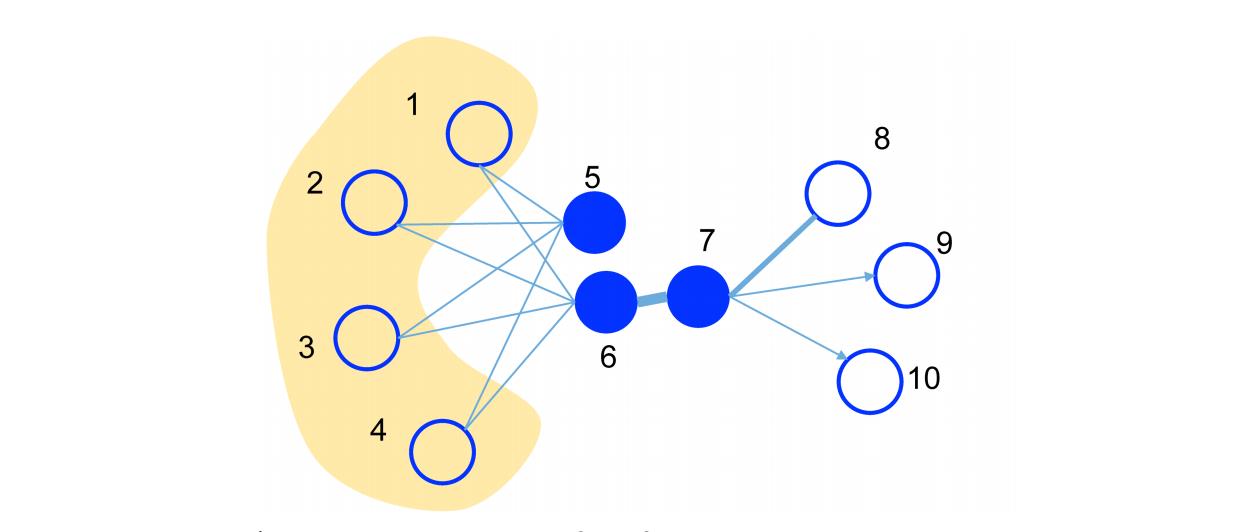
1、一阶相似度
一阶相似度用来描述的是两个顶点之间有一条边直接相连的情况,如果两个 u 、 v u、v u、v 之间存在直连变,则其一阶相似度可以用权重 w u v w_uv wuv来表示,如果不存在直连边,则一阶相似度为0。
上图中,顶点6、7之间是直接相连的,且权重比较大(边比较粗),则认为顶点6、7是相似的,且一阶相似度较高,顶点5、6之间并没有直接相连,则两者的一阶相似度为0。
2、二阶相似度
二阶相似度描述的是两个顶点之间没有直接相连,但是他们拥有相同的邻居。比如顶点 u 、 v u、v u、v 直接不存在直接相连,但是 顶点 u u u 存在其自己的一阶连接点, u u u 和 对应的一阶连接点 的一阶相似度可以形式化定义为: p ( u ) = ( w u , 1 , . . . , w u , ∣ V ∣ ) p(u) = (w_u,1, ..., w_u, |V|) p(u)=(wu,1,...,wu,∣V∣) ,同理可以得到顶点 v v v 和对应的一阶连接点的一阶相似度定义: p ( v ) = ( w v , 1 , . . . , w v , ∣ V ∣ ) p(v) = (w_v,1, ..., w_v, |V|) p(v)=(wv,1,...,wv,∣V∣) ,顶点 u 、 v u、v u、v 之间的相似度即为 p ( u ) 、 p ( v ) p(u)、p(v) p(u)、p(v) 之间的相似度。
上图中,顶点 5、6之间并没有直接相连,但是他们各自的一阶连接点是相同的,说明他们也是相似的。二阶相似度就是用来描述这种关系的。
2.2 优化目标
1、一阶相似度
对于每一条无向边
(
i
,
j
)
(i,j)
(i,j) ,定义顶点
v
i
,
v
j
v_i, v_j
vi,vj之间的联合概率为:
p
1
(
v
i
,
v
j
)
=
1
1
+
e
x
p
(
−
u
i
⃗
⋅
u
j
⃗
)
p_1(v_i,v_j) = \\frac1 1+exp(- \\vecu_i \\cdot \\vecu_j)
p1(vi,vj)=1+exp(−ui⋅uj)1
其中
u
i
⃗
∈
R
d
\\vecu_i \\in R^d
ui∈Rd 为顶点
v
i
v_i
vi 的低维向量表示(可以看作一个内积模型,计算两个item之间的匹配程度)。
同时定义经验分为:
p
^
1
(
i
,
j
)
=
w
i
,
j
W
\\hatp_1(i,j) = \\fracw_i,jW
p^1(i,j)=Wwi,j
其中
W
=
∑
i
,
j
∈
E
w
i
,
j
W = \\sum_i,j \\in E w_i,j
W=∑i,j∈Ewi,j。
为了计算一阶相似度,优化的目标函数为:
O
1
=
d
(
p
^
1
(
⋅
,
⋅
)
,
p
1
(
⋅
,
⋅
)
)
O_1 = d(\\hatp_1(\\cdot , \\cdot), p_1(\\cdot , \\cdot))
O1=d(p^1(⋅,⋅),p1(⋅,⋅))
其中
d
(
⋅
,
⋅
)
d(\\cdot , \\cdot)
d(⋅,⋅) 是两个分布的距离,常用的衡量两个概率分布差异的指标为 KL 散度,使用 KL 散度并忽略常用项后有:
O
1
=
−
∑
(
i
,
j
)
∈
E
w
i
,
j
l
o
g
p
1
(
v
i
,
v
j
)
O_1 = - \\sum_(i,j) \\in E w_i,j log \\, p_1 (v_i, v_j)
O1=−(i,j)∈E∑wi,jlogp1(vi,vj)
一阶相似度只能用于无向图中。
2、二阶相似度
和一阶相似度不同的是,二阶相似度既可以用于无向图,也可以用于有向图。二阶相似度计算的假设前提是:两个顶点共享其各自的一阶连接顶点,在这种情况下,顶点被看作是一种特定的「上下文」信息,因此每一个顶点都扮演了两个角色,即拥有两个embedding向量,一个是顶点本身的表示向量,一个是该点作为其他顶点的上下文顶点时的表示向量。
对于有向边
(
i
,
j
)
(i,j)
(i,j),定义给定顶点
v
i
v_i
vi 的条件下,产生上下文(邻居)顶点
v
j
v_j
vj 的概率为:
p
2
(
v
j
∣
v
i
)
=
e
x
p
(
u
j
⃗
T
⋅
u
i
⃗
)
∑
k
=
1
∣
V
∣
e
x
p
(
u
k
⃗
T
⋅
u
i
⃗
)
p_2(v_j|v_i) = \\frac exp(\\vecu_j^T \\cdot \\vecu_i) \\sum_k=1^|V| exp(\\vecu_k^T \\cdot \\vecu_i)
p2(vj∣vi)=∑k=1∣V∣exp(ukT⋅ui)exp(ujT⋅