最优化之凸集凸函数上确界Jensen不等式共轭函数Fenchel不等式拉格朗日乘子法KKT条件
Posted dqhl1990
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了最优化之凸集凸函数上确界Jensen不等式共轭函数Fenchel不等式拉格朗日乘子法KKT条件相关的知识，希望对你有一定的参考价值。
最优化之凸集、凸函数、上确界、Jensen不等式、共轭函数、Fenchel不等式、拉格朗日乘子法、KKT条件、拉格朗日对偶
1.直线的向量表达
1.1 共线定理
对于任意两个向量 a ⃗ , b ⃗ \\veca, \\vecb a,b且 b ⃗ ≠ 0 \\vecb \\neq 0 b̸=0，当 a ⃗ ∣ ∣ b ⃗ \\veca||\\vecb a∣∣b时，存在唯一实数 λ \\lambda λ，使得 a ⃗ = λ b ⃗ \\veca=\\lambda \\vecb a=λb
1.2 共面定理
如果两个向量
a
⃗
,
b
⃗
\\veca,\\vecb
a,b不共线，则向量
p
⃗
\\vecp
p与向量
a
⃗
,
b
⃗
\\veca,\\vecb
a,b共面的充要条件是存在唯一的实数对
x
,
y
x,y
x,y，使得
p
⃗
=
x
a
⃗
+
y
b
⃗
\\vecp=x\\veca + y\\vecb
p=xa+yb
1.3 直线的向量参数方程
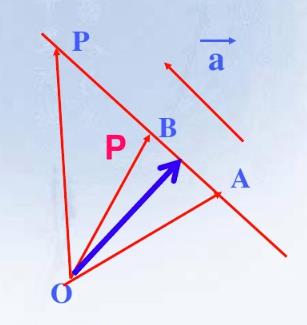
使用上图作为参考，我们得到： 以上是关于最优化之凸集凸函数上确界Jensen不等式共轭函数Fenchel不等式拉格朗日乘子法KKT条件的主要内容，如果未能解决你的问题，请参考以下文章 深度学习/机器学习入门基础数学知识整理：Jensen不等式简单理解，共轭函数
对于直线上任意第一点
P
P
P，我们有
A
P
⃗
=
θ
A
B
⃗
\\vecAP = \\theta\\vecAB
AP=θAB
(1)
O
P
⃗
=
O
A
⃗
+
A
P
⃗
=
O
A
⃗
+
θ
A
B
⃗
=
O
A
⃗
+
θ
(
A
O
⃗
+
O
B
⃗
)
=
O
A
⃗
+
θ
A
O
⃗
+
θ
O
B
⃗
=
O
A
⃗
−
θ
O
A
⃗
+
θ
O
B
⃗
=
(
1
−
θ
)
O
A
⃗
+
θ
O
B
⃗
\\beginaligned \\vecOP &= \\vecOA + \\vecAP \\\\ &= \\vecOA + \\theta\\vecAB\\\\ &= \\vecOA + \\theta(\\vecAO + \\vecOB) \\\\ &= \\vecOA +\\theta \\vecAO + \\theta \\vecOB\\\\ &=\\vecOA - \\theta \\vecOA + \\theta \\vecOB\\\\ &= (1 - \\theta) \\vecOA + \\theta \\vecOB\\\\ \\tag1 \\endaligned
OP=OA+AP=OA+θAB=OA+θ(AO+OB)=OA+θAO+θOB=OA−θOA+θOB=(1−θ)OA+θOB(1)
设
O
O
O为原点
(
0
,
0
)
(0,0)
(0,0)，假设
A
A
A点坐标为
(
5
,
1
)
(5,1)
(5,1)，
B
B
B点坐标为
(
2