树堆（Treap）

Posted 2022-11-24 Code--Dream

平衡树

简介：

平衡二叉树（Balanced Binary Tree）具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

Treap：

简介：

Treap代码实现相对简单的一个算法，Treap是 heap+Tree，既满足堆的性质也满足平衡树的性质，一棵树的节点上有一个data用于存数据，fix是一个堆的优先级（假设我们是小顶堆），key是平衡树的比较值；key一般是给出的，然而fix我们随机生成，这样的随机会使得平衡树比较平衡。假设一棵排序二叉树插入一组有序的数，就会使得树退化为一条链。我们在插入的时候为每个节点随机生成一个fix（优先级）。插入时满足排序二叉树的性质。插入完成时检查是否满足堆的性质，并进行旋转操作使他满足堆的性质。

旋转操作：

为了满足堆的性质，我们需要对这棵树进行旋转以达到堆的性质。旋转操作看图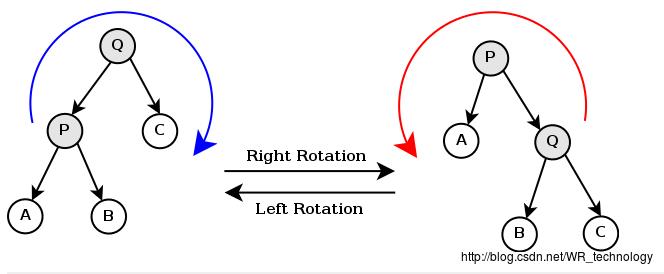
如图是旋转操作，我用的是指针链式的写法：所以，每次旋转需要调整两个节点的父子关系。以及指向P或者Q的那个指针。 下面给出指针的写法

void rotate(Node* &o,int d)

    Node *k=o->ch[d^1];
    o->ch[d^1]=k->ch[d];
    k->ch[d]=o;
    o=k;

上面是旋转操作，d传0代表左旋，d为1代表右旋；
当我们了解旋转操作后，接下来；

插入元素操作：

首先根据排序二叉树的性质找到叶子节点，将新的元素插入到叶子节点。当插入之后会破坏堆的性质，然后进行旋转操作让他满足堆的性质，因为那样旋转不会破坏排序二叉树的性质的。所以旋转只需要考虑堆的性质。

删除操作：

用排序二叉树的性质去找要删除的元素位置，找到之后判断是否左右都是有儿子，如果不是直接删除，把指向他的指针，直接指向他的儿子节点。如果是就需要通过旋转操作。把需要删除的元素往下旋转。旋转时为了满足堆的性质（如果是小顶堆）需要比较左右儿子的大小，将该元素与小值的儿子进行旋转。

题目链接：https://vjudge.net/problem/POJ-3481

#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int sz;
const int maxn=1e6+10;
struct Node

    Node *ch[2];
    int r,v,info;//v是顾客优先级,info是顾客的编号,r由rand()生成
    int cmp(int x)
    
        if(x==v) return -1;
        return x<v? 0:1;
    
T[maxn];
Node * newnode(int _v,int _info)

    Node *res=&T[sz];
    T[sz].v=_v,T[sz].info=_info;
    T[sz].r=rand();
    T[sz].ch[0]=T[sz].ch[1]=NULL;
    sz++;
    return res;

void rotate(Node* &o,int d)

    Node *k=o->ch[d^1];
    o->ch[d^1]=k->ch[d];
    k->ch[d]=o;
    o=k;

void insert(Node* &o,int v,int info)

    if(o==NULL) o=newnode(v,info);
    else
    
        int d= v < o->v?0:1;
        insert(o->ch[d],v,info);
        if(o->ch[d]->r > o->r)
            rotate(o,d^1);
    

void remove(Node *&o,int v)

    int d=o->cmp(v);
    if(d==-1)
    
        if(o->ch[0] && o->ch[1])
        
            int d2 = o->ch[0]->r < o->ch[1]->r ?0:1;
            rotate(o,d2);
            remove(o->ch[d2],v);
        
        else
        
            if(o->ch[0]==NULL)o=o->ch[1];
            else o=o->ch[0];
        
    
    else remove(o->ch[d],v);

int find_max(Node *o)//找到最大v值

    if(o->ch[1]==NULL)
    
        printf("%d\\n",o->info);
        return o->v;
    
    return find_max(o->ch[1]);

int find_min(Node *o)//找到最小v值

    if(o->ch[0]==NULL)
    
        printf("%d\\n",o->info);
        return o->v;
    
    return find_min(o->ch[0]);

int main()

    int op;
    Node *root=NULL;
    sz=0;
    while(scanf("%d",&op)==1&&op)
    
        if(op==1)
        
            int info,v;
            scanf("%d%d",&info,&v);
            insert(root,v,info);
        
        else if(op==2)
        
            if(root==NULL)
            
                printf("0\\n");
                continue;
            
            int v=find_max(root);
            remove(root,v);
        
        else if(op==3)
        
            if(root==NULL)
            
                printf("0\\n");
                continue;
            
            int v=find_min(root);
            remove(root,v);
        
    
    return 0;

优先队列的实现。